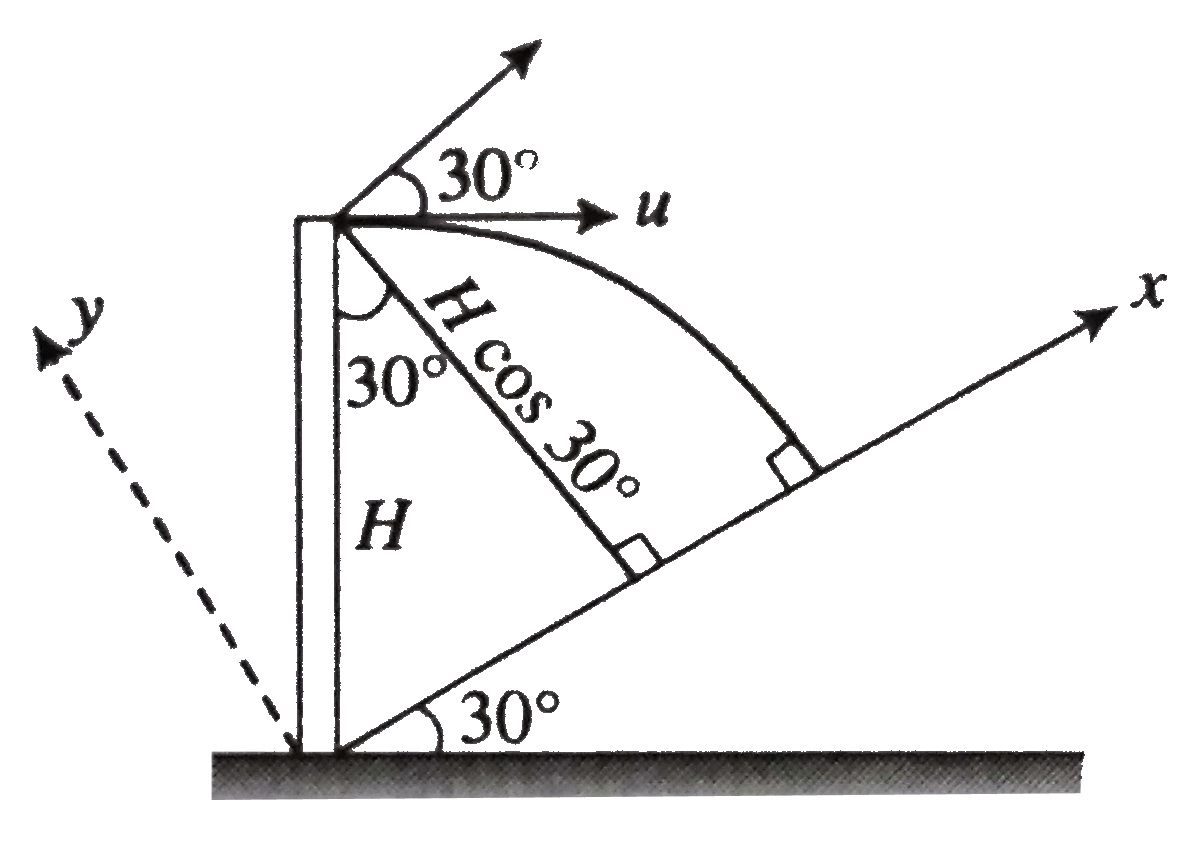
In figure, find the horizontal velocity u(∈ms−1) of a projectile so that it hits the inclined plane perpendicularly. Given H=6.25m.

The correct Answer is:5
vx=ux+axt
⇒0=ucos30∘−gsin30∘t
⇒t=u√3g
Sy=uyt+12ayt2
⇒−Hcos30∘=−usin30∘t
−12gcos30∘t2
⇒−H√32=−u2u√3g−12g√32u23g2
⇒u=√2gH/5=√2×10×6.25/5=5ms−1.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Fill in the blanks
Explore 4 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:True or False
Explore 2 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Linked Comprehension Type
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
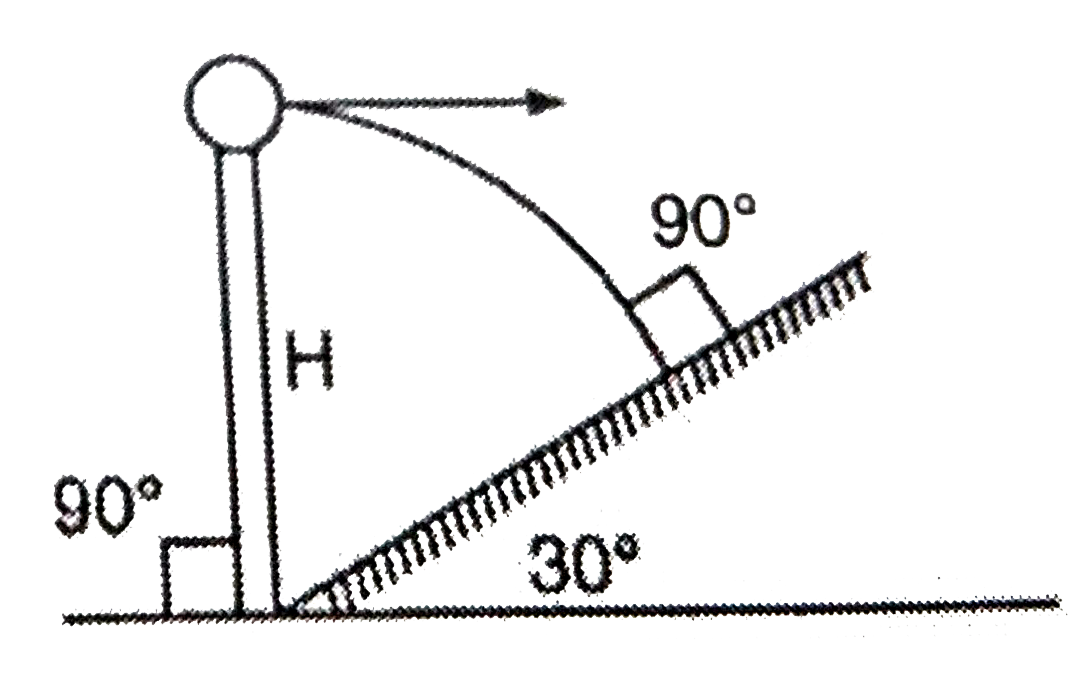
In the given figure , the angle of inclination of the inclined plane is 30∘. A particle is projected with horizontal velocity v0 from height H. Find the horizotnal velocity v0 (in m/s) so that the particle hits the inclined plane perpendicu lar .Given H=4m, g=10m/s2.
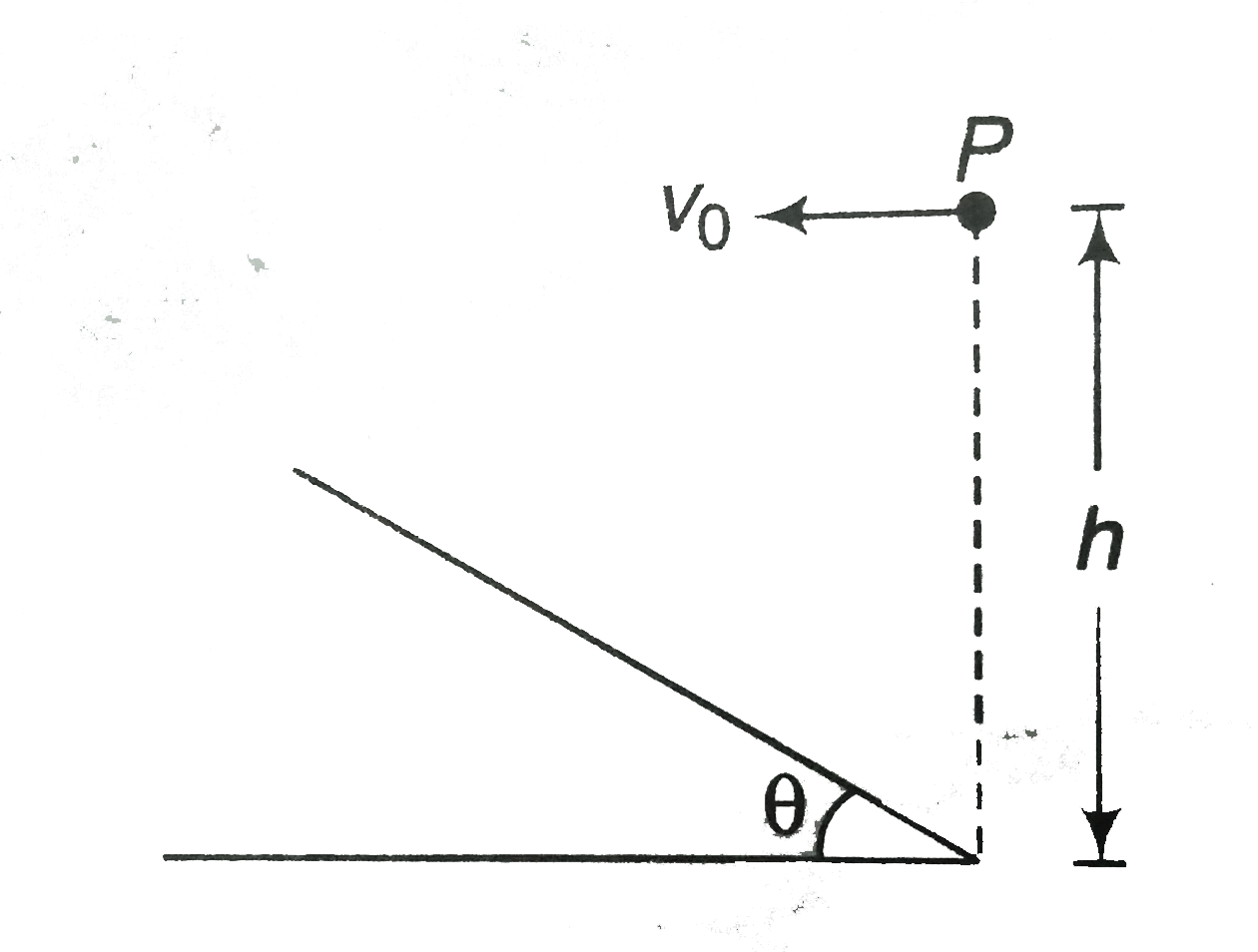
View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
View Solution
Knowledge Check
In figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 . AV0=√2gH5BV0=√2gH7CV0=√gH5DV0=√gH7
. AV0=√2gH5BV0=√2gH7CV0=√gH5DV0=√gH7Two inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10(√3)ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate

The velocity with which particle strikes the plane OB,A15ms−1B30ms−1C20ms−1D10ms−1Two inclined planes OA and OB having inclination (with horizontal) 30∘and60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10√3ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
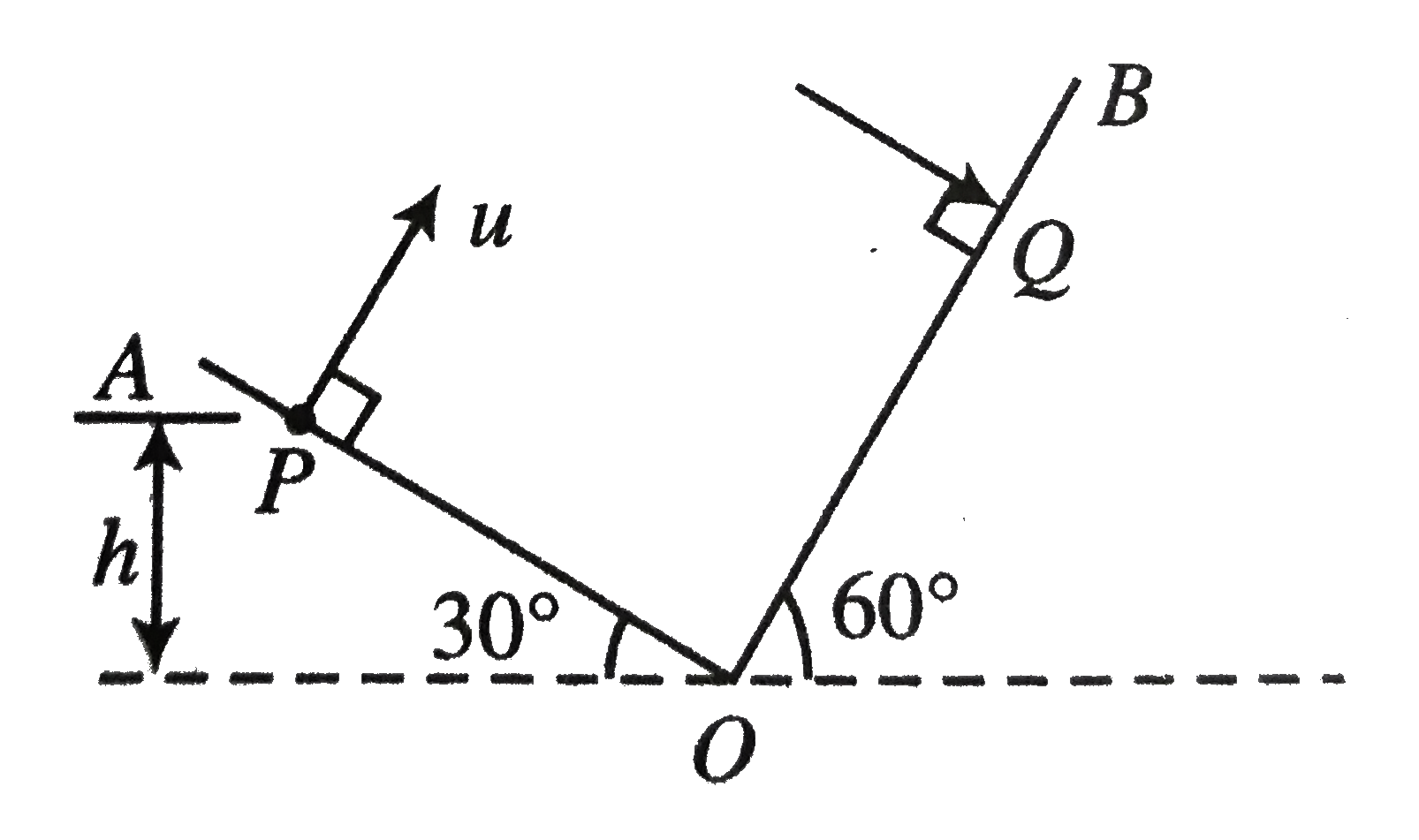
The vertical height h of P from O,A10 mB5 mC15 mD20 m
A projectile is thrown at an angle θ with an inclined plane of inclination β as shown in fig. 1E108. Find the relation between β and θ ifv :
(a)projectile strikezs the inclined plane perpendicularly,
(b) projectile strikes the inclined plane horizontal.
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA particle is thrown horizontally with velocity 10 m/s from an incline of inclination 30∘ , it hits on the incline agin then displacement (in m) of the particle is:
View SolutionTwo inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘(), respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10√3ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
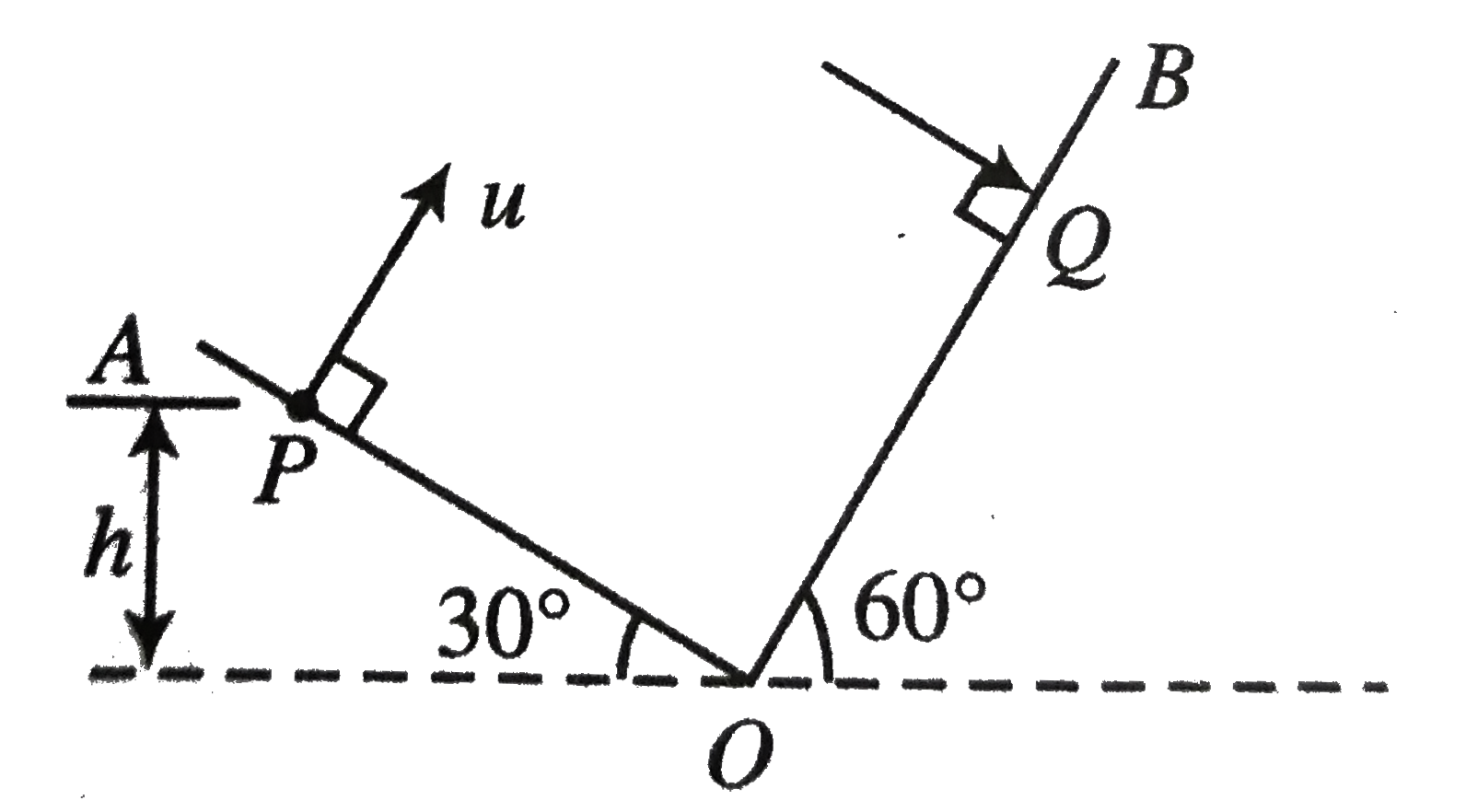
The maximum height attained by the particle (from the line O)
View SolutionTwo inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10(√3)ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
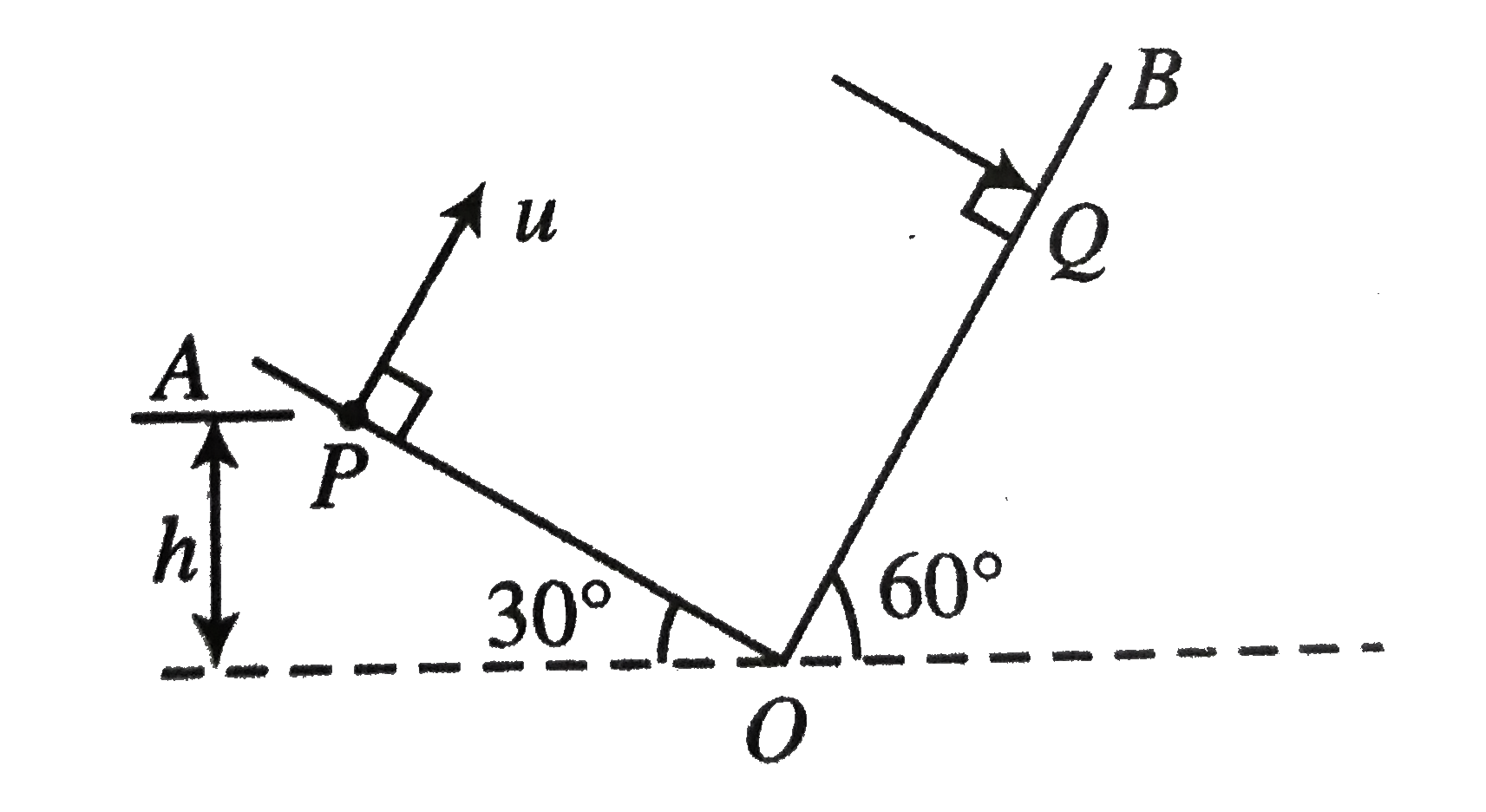
The distance PQ,
View Solution

