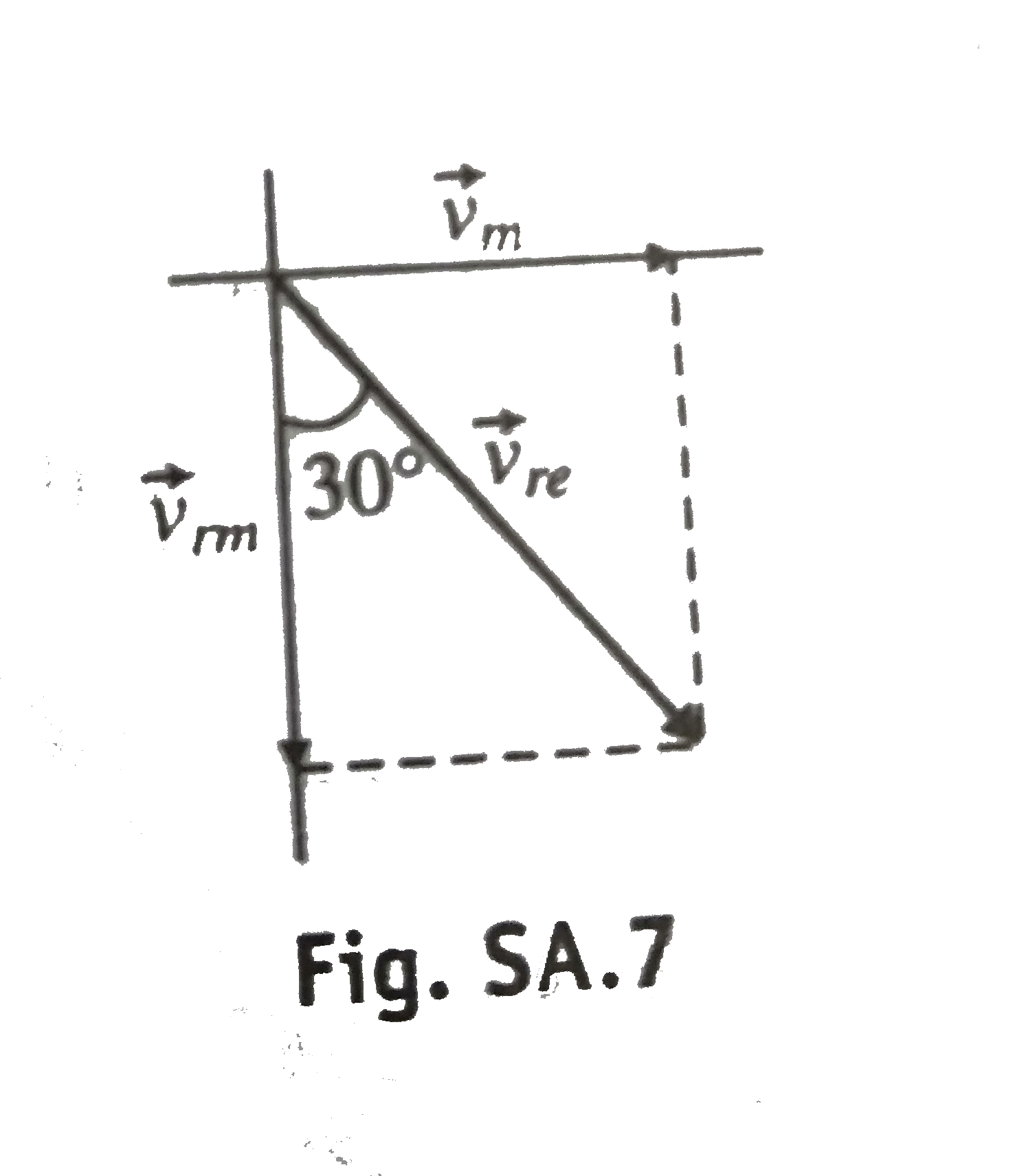
A man holds an umbrella at 30∘ with the vertical to keep himself dry. He, then, runs at a speed of 10ms−1, and find the rain drops to be hitting vertically. Study the following statement and find the correct options.
i. Velocity of rain w.r.t. Earth is 20ms−1
ii. Velocity of rain w.r.t. man is 10√3ms−1.
iii. Velocity of rain w.r.t. Earth is 30ms−1
iv. Velocity of rain w.r. t. man is 10√2ms−1 .
Statements (i) and (ii) are correct.
Statements (i) and (iii) are correct.
Statements (iii) and (iv) are correct.
Statements (ii) and (iv) are correct.
The correct Answer is:A
a. →vm=Velocityofman
→vre = Velocity of rain w.r.t. earth
→vrm = Velocity of rain w.r.t. man
Velocity of man |→vm|=10ms−1
Using sin30∘=vmvre
vre=vmsin30∘=101/2=20ms−1.
cos30∘=vrmvre
vrm=vrecos30=20×√32=10√3ms−1.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
For a particle moving along the x-axis, mark the correct statement(s).
View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00 (hh:mm:ss:100 th part of the second). Find the value of g. (correct upt ot two decimal places).
View SolutionThe springs shown in the figure are all upstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block.

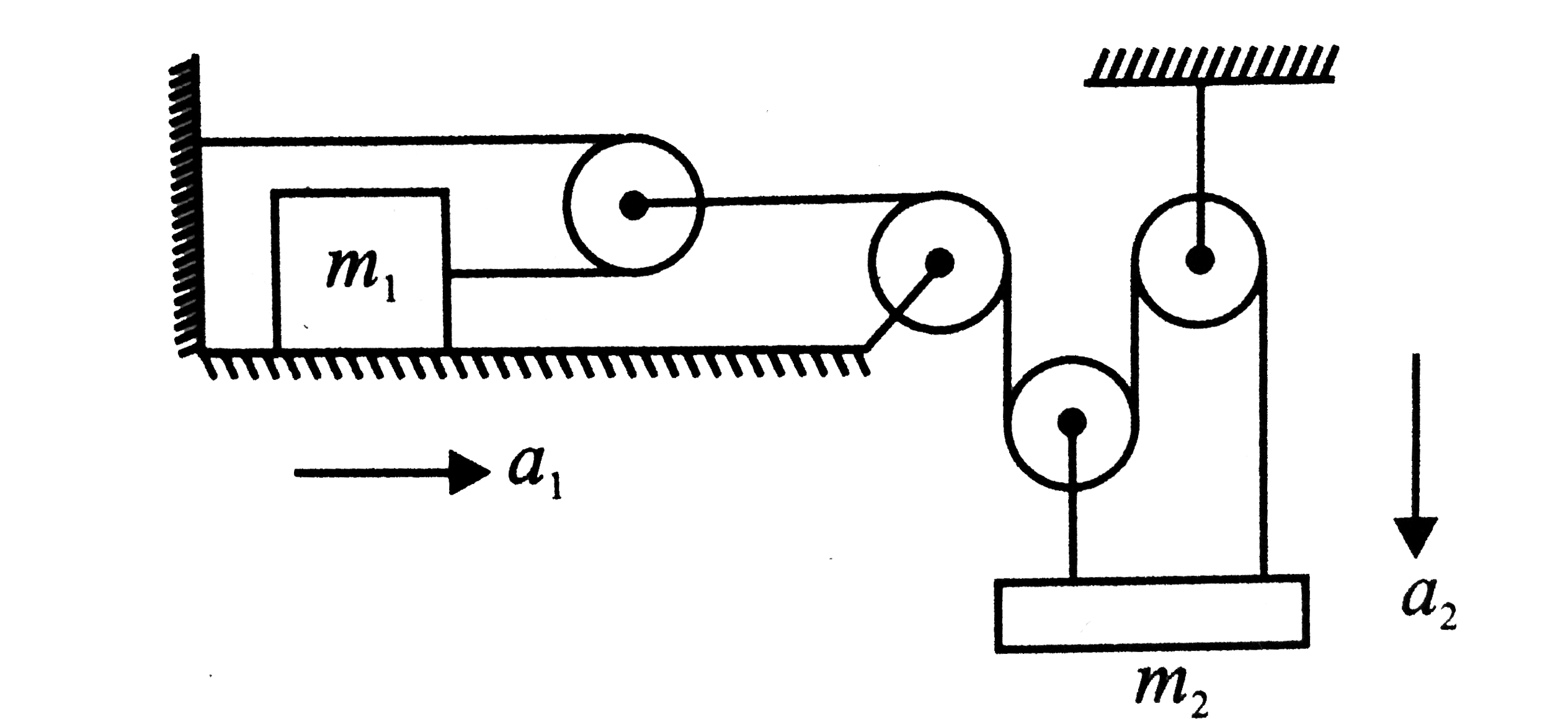
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
View SolutionTo a man running upwards on the hill, the rain appears to fall vertically downwards with 4ms−1. The velocity vector of the man w.r.t. earth is (2ˆi+3ˆj)ms−1. If the man starts running down the hill with the same speed, then determine the relative speed of the rain w.r.t. man.
 .
.
View SolutionRain is falling vertically with a velocity of 3 kmh^-1 . A man walks in the rain with a velocity of 4 kmh^-1 . The rain drops will fall on the man with a velocity of
View SolutionA man standing on a road has to hold his umbrella at 30∘ with the vertical to keep the rain away. He throws the umbrella and starts running at 10km/hr. He finds that rain drop are hitting his head vertically. Find the speed of rain drops with respect to (a) road (b) the moving man.
View SolutionA man is moving due east with a speed 1 km/hr and rain is falling vertically with a speed √3 km/hr. At what angle from vertical the man has to hold his umbrella to keep the rain away. Also find the speed of rain drops w.r.t. man.
View SolutionA person is standing on a road with his umbrella open at 30^@ with the vertical to save himself from rain . Then he starts moving at 5 km *h^(-1) . Now the finds that rain drops are hitting his umbrella vertically. Find the speed of rain drops w.r.t(i) the road .(ii) the moving person.
View SolutionIt is raining at a speed of 5ms−1 at an angle 37∘ to vertical, towards east. A man is moving to west with a velocity of 5ms−1. The angle with the vertical at which he has to hold the umbrella to protect himself from rain is
View SolutionIt is raining at a speed of 5ms−1 at an angle 37∘ to vertical, towards east. A man is moving to west with a velocity of 5ms−1 . The angle with the vertical at which he has to hold the umbrella to protect himself from rain is
View SolutionIt is raining at a speed of 5 ms^(-1) at an angle 37^@ to vertical, towards east. A man is moving to west with a velocity of 5 ms^(-1) . The angle with the vertical at which he has to hold the umbrella to protect himself from rain is
View SolutionA person standing on a road has to hold his umbrella at 600 with the verticcal to keep the rain away. He throws the umbrella an starts running at 20ms−1. He finds that rain drops are hitting his head vertically. Find the speed of the rain drops with respect to (a) the road (b) the moving person.
View SolutionTo a man running upwards on the hill, the rain appears to fall vertically downwards with 4ms−1. The velocity vector of the man w.r.t. earth is (2ˆi+3ˆj)ms−1. If the man starts running down the hill with the same speed, then determine the relative speed of the rain w.r.t. man.
 .
.
View SolutionA man holds an umbrella at 30^@ with the vertical to keep himself dry. He, then, runs at a speed of 10ms^(-1) , and find the rain drops to be hitting vertically. Study the following statement and find the correct options. i. Velocity of rain w.r.t. Earth is 20 ms^(-1) ii. Velocity of rain w.r.t. man is 10 sqrt(3)ms^(-1) . iii. Velocity of rain w.r.t. Earth is 30 ms^(-1) iv. Velocity of rain w.r. t. man is 10sqrt(2) ms^(-1) .
View Solution
