Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
va
2av
2av(2+√3)
2av(2−√3)
The correct Answer is:D
d. t=av−vcosπn.Heren=12

⇒t=av−vcos(2π12)=2av(2−√3).
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
six particles are situated at the corners of a regular hexagon. These particles start moving with equal speed of 10 m/s in such that velocity of any one particle is directed towards the next particle. Find the rate (in m/s) at which length of a side of the hexagon is decreasing.
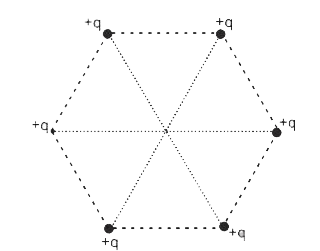
View SolutionSix equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
View Solution
Knowledge Check
Four particles situated at the corners of a square of side ‘a’ move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.
AavBa2vCa3vD2a3vThree particles of masses 1kg,2kg and 3kg are situated at the corners of an equilateral triangle move at speed 6ms−1,3ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particles at the next corners symmetrically. Find velocity of CM of the system at this instant
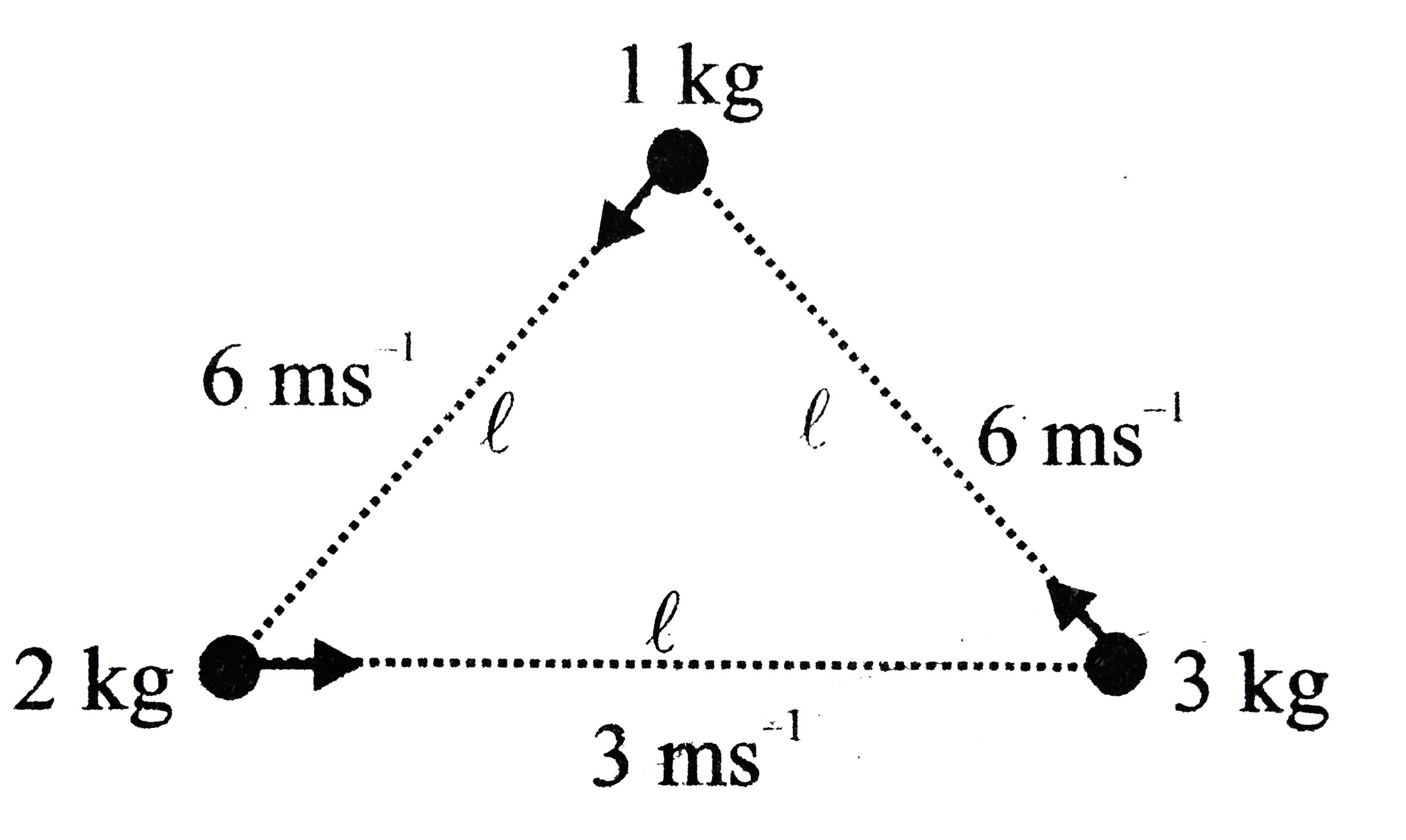 A3ms−1B5ms−1C6ms−1Dzero
A3ms−1B5ms−1C6ms−1DzeroFour particles of masses 1 kg, 2 kg, 3 kg, and 4 kg are situated at the corners of a square and moving at speed 3ms−1,4ms−1,1ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particle at the next comer symmetrically. The momentum of the system at this instant is
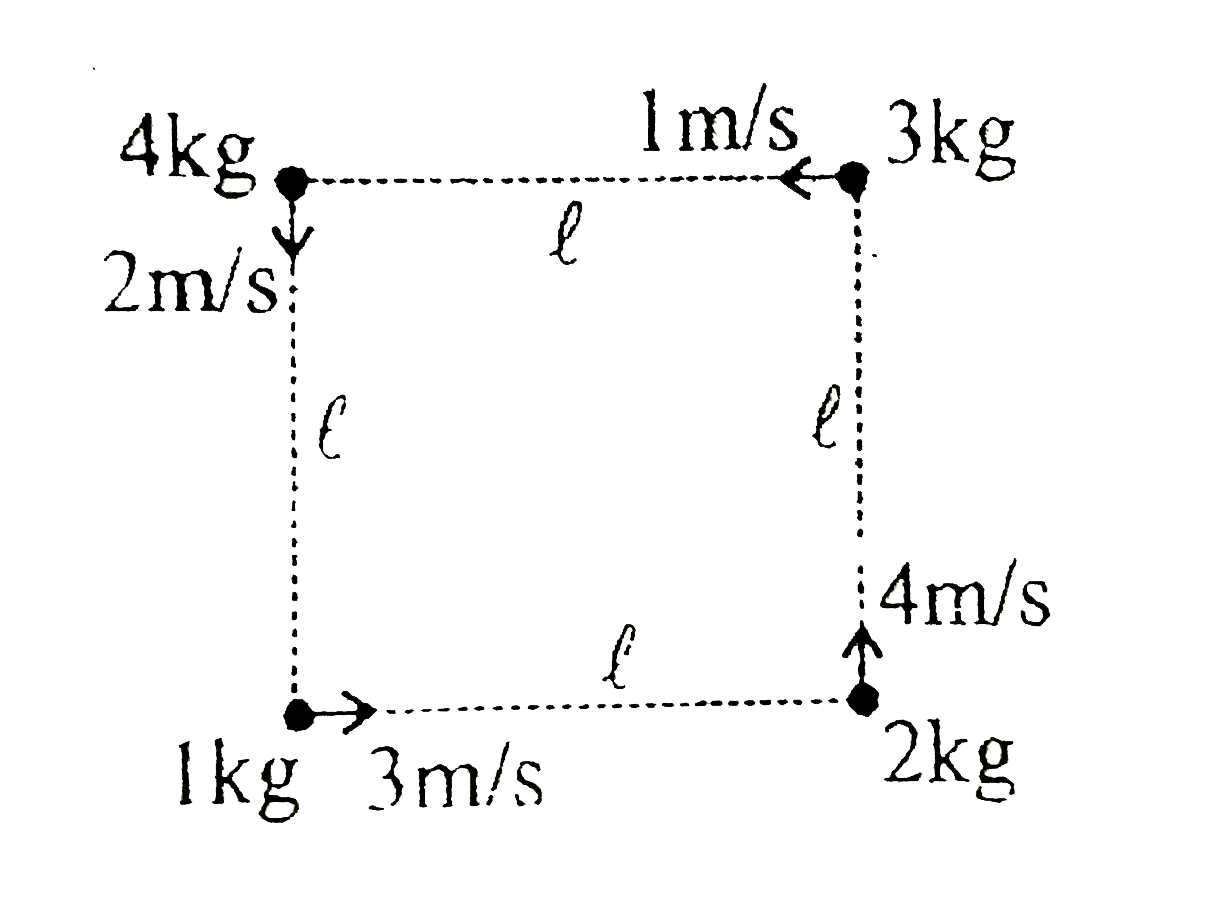 A3kgms−1B5kgms−1C6kgms−1DZero
A3kgms−1B5kgms−1C6kgms−1DZero
Four particles A,B,CandD are situated at the cornerst of a square ABCD of side aatt−0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CB~andD along DA. At what time will these particles meet each other ?
View SolutionSix identical particles each of mass m are arranged at the corners of a regular hexagon of side length L. If the mass of one of the particle is doubled, the shift in the centre of mass is
View SolutionA particle is moving in a circle with a constant speed, the acceleration of the particle has
View SolutionSix particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
View SolutionA particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate
View Solution
