Three identical balls each of radius 10 cm and mass 1 kg each are placed touching one another on a horizontal surface. Where is their centre of mass located?
On the horizontal surface
At the point of contact of any two spheres
At the centre of one ball
none of these
The correct Answer is:D
To find the center of mass of three identical balls placed touching one another on a horizontal surface, we can follow these steps:
Step 1: Understand the Setup
We have three identical balls, each with a radius of 10 cm and a mass of 1 kg. They are arranged in a way that they touch each other.
Step 2: Position the Balls
Let's position the balls in a coordinate system for easier calculation. We can place the centers of the balls as follows:
- Ball 1: Center at (0, 0)
- Ball 2: Center at (20 cm, 0) — since the radius is 10 cm, the distance between the centers of the two balls is 20 cm.
- Ball 3: Center at (10 cm, 20 cm) — this ball will be placed above the midpoint between the first two balls.
Step 3: Calculate the Center of Mass
The center of mass (CM) can be calculated using the formula:
xcm=∑mixi∑mi
ycm=∑miyi∑mi
Where mi is the mass of each ball and (xi,yi) are the coordinates of their centers.
For our three balls:
- m1=m2=m3=1kg
- Coordinates:
- Ball 1: (0,0)
- Ball 2: (20,0)
- Ball 3: (10,20)
Calculating xcm:
xcm=(1⋅0)+(1⋅20)+(1⋅10)1+1+1=0+20+103=303=10cm
Calculating ycm:
ycm=(1⋅0)+(1⋅0)+(1⋅20)1+1+1=0+0+203=203≈6.67cm
Step 4: Conclusion
The center of mass of the three balls is located at the coordinates (10cm,203cm), which is approximately (10cm,6.67cm) above the horizontal surface.
We have three identical balls, each with a radius of 10 cm and a mass of 1 kg. They are arranged in a way that they touch each other.
Let's position the balls in a coordinate system for easier calculation. We can place the centers of the balls as follows:
- Ball 1: Center at (0, 0)
- Ball 2: Center at (20 cm, 0) — since the radius is 10 cm, the distance between the centers of the two balls is 20 cm.
- Ball 3: Center at (10 cm, 20 cm) — this ball will be placed above the midpoint between the first two balls.
The center of mass (CM) can be calculated using the formula:
xcm=∑mixi∑mi
ycm=∑miyi∑mi
Where mi is the mass of each ball and (xi,yi) are the coordinates of their centers.
- m1=m2=m3=1kg
- Coordinates:
- Ball 1: (0,0)
- Ball 2: (20,0)
- Ball 3: (10,20)
xcm=(1⋅0)+(1⋅20)+(1⋅10)1+1+1=0+20+103=303=10cm
ycm=(1⋅0)+(1⋅0)+(1⋅20)1+1+1=0+0+203=203≈6.67cm
The center of mass of the three balls is located at the coordinates (10cm,203cm), which is approximately (10cm,6.67cm) above the horizontal surface.
Topper's Solved these Questions
Similar Questions
In the figure shown, the two identical balls of mass M and radius R each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass M and radius R2' is coming down vertically and has a velocity =υ0 when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to :

View SolutionThree identical spheres each of radius 3cm are placed on a horizontal surface touching one another. The distance of centre of mass of system from any centre of the sphere is
View Solution
Knowledge Check
Four identical spheres each of radius 10 cm and mass 1 kg are placed on a horizontal surface touching one another so that their centres are located at the corners of square of side 20 cm. What is the distance of their centre of mass from centre of either sphere ?
A5 cmB10 cmC20 cmDNone of theseThree identical spheres each of radius R are placed touching each other on a horizontal table as shown in figure. The co-ordinates of centre of mass are :
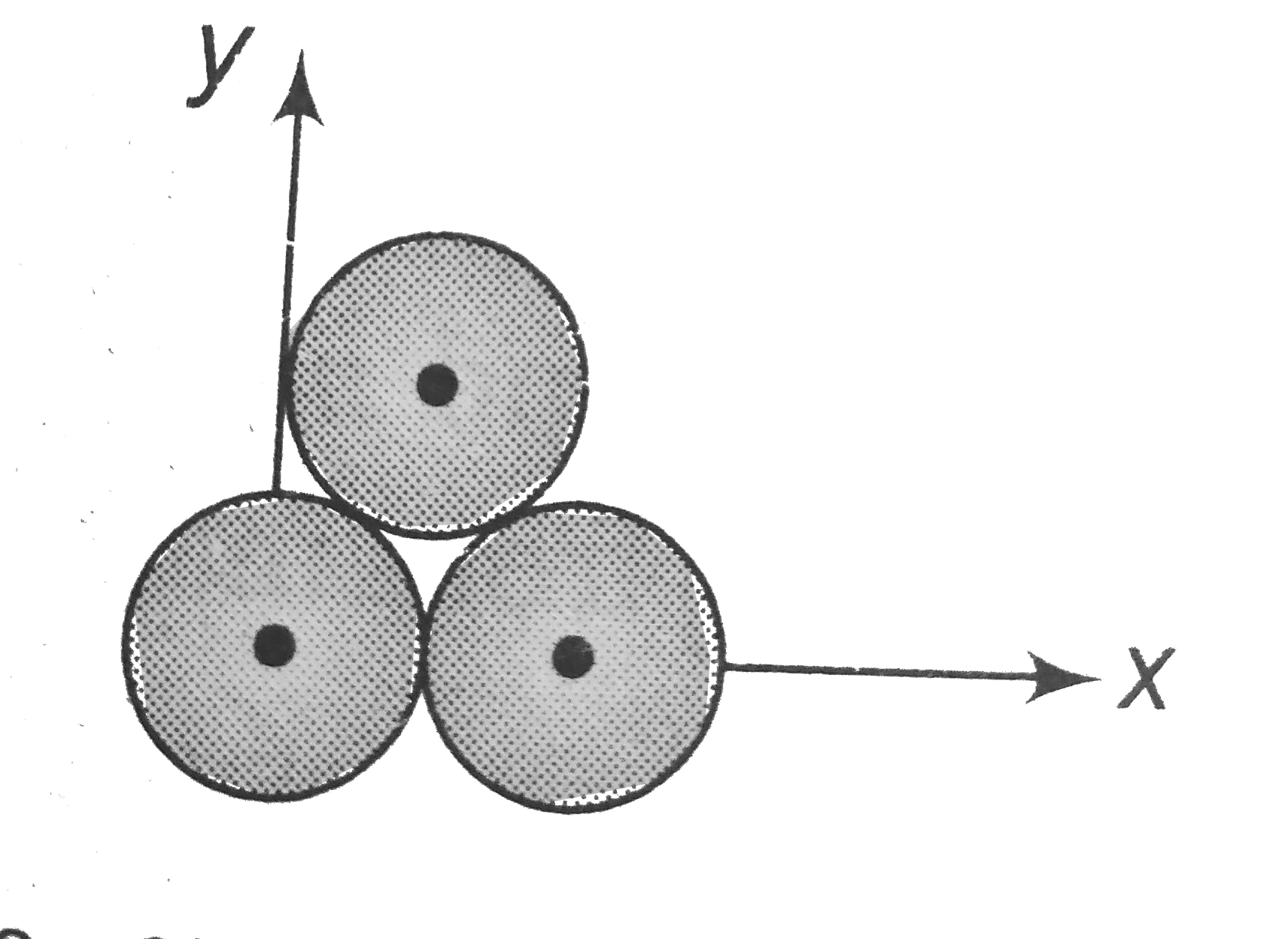 .A(R,R)B(0,0)C(R2,R2)D(R,R√3)
.A(R,R)B(0,0)C(R2,R2)D(R,R√3)Three identical metal balls, each of the radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed when centres of three balls are joined. The centre ofthe mass of the system is located at
Aline joining centres of any two ballsBcentre of one of the ballsChorizontal surfaceDhorizontal surface
Three thin unifrom circular discs each of mass M and radius R are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three discs are joined. Find the M.I. about an axis passing through the center of mass system of discs and perpendicular to the plane.
View SolutionThree identical metal balls each of radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three balls are joined. The center of mass of system is located at the
View SolutionIn the figure shown, the two identical balls of mass M and radius R each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass M and radius R/2, is coming down vertically and has a velocity =v0 when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to

View SolutionIn the figure shown, the two identical balls of mass M and radius R each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass M and radius R2' is coming down vertically and has a velocity =υ0 when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to :

View SolutionTwo identical spheres of radius 2 cm and mass 1 kg are placed 1 cm apart on the surface of the earth. Then,
View Solution
