Number of beats between A and B is 5 and between B and C are 3. Number of beats between A and C may be
1
2
8
Both B and C
The correct Answer is:D
To solve the problem of finding the number of beats between A and C, given the number of beats between A and B is 5 and between B and C is 3, we can follow these steps:
Step 1: Understand the Concept of Beats
The number of beats is defined as the absolute difference in frequencies of two waves. If the number of beats between A and B is 5, we can express this mathematically as:
|fA−fB|=5
This means that the frequency of A (f_A) can be either 5 units higher or lower than the frequency of B (f_B).
Step 2: Set Up the Equations
From the information given:
1. fA−fB=5 or fB−fA=5
2. The number of beats between B and C is 3, so:
|fB−fC|=3
This gives us two more equations:
- fB−fC=3 or fC−fB=3
Step 3: Analyze the Cases
We will analyze the possible cases based on the relationships between the frequencies.
Case 1: fA−fB=5 and fB−fC=3
From these equations:
- fA=fB+5
- fB=fC+3
Substituting the second equation into the first:
fA=(fC+3)+5=fC+8
Thus, |fA−fC|=8 (which means 8 beats).
Case 2: fA−fB=5 and fC−fB=3
From these equations:
- fA=fB+5
- fC=fB+3
Substituting:
fA=(fB−3)+5=fB+2
Thus, |fA−fC|=2 (which means 2 beats).
Case 3: fB−fA=5 and fB−fC=3
From these equations:
- fB=fA+5
- fB=fC+3
Substituting:
fC=fB−3=(fA+5)−3=fA+2
Thus, |fA−fC|=2 (which means 2 beats).
Case 4: fB−fA=5 and fC−fB=3
From these equations:
- fB=fA+5
- fC=fB+3
Substituting:
fC=(fA+5)+3=fA+8
Thus, |fA−fC|=8 (which means 8 beats).
Step 4: Conclusion
From the analysis, we find that the number of beats between A and C can be either 2 or 8.
Final Answer
The number of beats between A and C may be 2 or 8.
---
The number of beats is defined as the absolute difference in frequencies of two waves. If the number of beats between A and B is 5, we can express this mathematically as:
|fA−fB|=5
This means that the frequency of A (f_A) can be either 5 units higher or lower than the frequency of B (f_B).
From the information given:
1. fA−fB=5 or fB−fA=5
2. The number of beats between B and C is 3, so:
|fB−fC|=3
This gives us two more equations:
- fB−fC=3 or fC−fB=3
We will analyze the possible cases based on the relationships between the frequencies.
From these equations:
- fA=fB+5
- fB=fC+3
fA=(fC+3)+5=fC+8
Thus, |fA−fC|=8 (which means 8 beats).
From these equations:
- fA=fB+5
- fC=fB+3
fA=(fB−3)+5=fB+2
Thus, |fA−fC|=2 (which means 2 beats).
From these equations:
- fB=fA+5
- fB=fC+3
fC=fB−3=(fA+5)−3=fA+2
Thus, |fA−fC|=2 (which means 2 beats).
From these equations:
- fB=fA+5
- fC=fB+3
fC=(fA+5)+3=fA+8
Thus, |fA−fC|=8 (which means 8 beats).
From the analysis, we find that the number of beats between A and C can be either 2 or 8.
The number of beats between A and C may be 2 or 8.
Topper's Solved these Questions
- WAVE MOTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:WAVE MOTIONExercise:Exercise 2
Explore 30 Videos
- WAVE MOTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:WAVE MOTIONExercise:MHT CET CORNER
Explore 23 Videos
- WAVE MOTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:WAVE MOTIONExercise:MHT CET CORNER
Explore 23 Videos
- SURFACE TENSION Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:SURFACE TENSION Exercise:MHT CET Corner
Explore 15 Videos
- WAVE THEORY OF LIGHT Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:WAVE THEORY OF LIGHT Exercise:MHT CET CORNER
Explore 4 Videos
Similar Questions
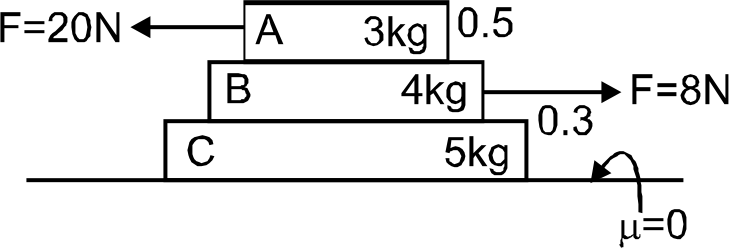
In the situation shown coefficient of friction between A and B is 0.5 and between B and C is 0.3 . Friction acting between B and C is xN then 9x7 is
View SolutionThe genes A,B,C and d are located on the same chromosome in such a way that the distance between A and B is 7 map units, between B an C is 2 map is unit, between C and D is. 4.5 units. What is the distance between A and D? What is the porbability of linkage between B and D and between A and D?
View Solution
Knowledge Check
Number of beats between A and B is 5 and between B and C are 3. Number of beats between A and C may be
A1B2C8DNoneRatio between A and B is 4 : 5 and between B and C is 2 : 3 .If A has 800 , then C has -
ARs. 1000BRs. 1200CRs. 1500DRs. 2000The bond between B and C will be
AIonicBColvalentCHydrogenDCoordinate
A B and C are three tuning forks.Frequency of A is 150Hz .Beats produced by A and B are 5 per second and by B and C are 3 per second.When the wax is put on A beat frequency between A and B is 2Hz and between A and C is 5Hz .Then find the frequency of B and C respectively.
View SolutionFind rational number between a and b .
View SolutionThe number of primes between 90 and 100 is 0 (b) 1 (c) 2 (d) 3
View Solution
Relation between (B) and (C) is:
View SolutionA,Band C are three tuning forks. Frequency of A is 350HZ . Beats produced by A and B are 5/s and by B and C are 4/s . When a wax is put on A beat frequency between A and B is 2HZ and between a and C is 6Hz . Then, frequency of B and C respectively , are
View Solution

