A particle is taken from point A to point B under the influence of a force field. Now it is taken back from B to A and it is observed that the work done in taking the particle from A to B is not equal to the work done in taking it from B to A. If $W_{n c}$ and $W_{c}$ are the work done by non-conservative and conservative forces present in the system, respectively, $Δ U$ is the change in potential energy and $Δ k$ is the change in kinetic energy, then

A

(a) $W_{n c} - Δ U = Δ k$

B

(b) $W_{c} = - Δ U$

C

(c) $W_{n c} + W_{c} = Δ k$

D

(d) $W_{n c} - Δ U = - Δ k$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A, B, C

To solve the problem, we need to analyze the situation based on the principles of work, energy, and the characteristics of conservative and non-conservative forces.
1. Understanding the Work-Energy Theorem:
The work-energy theorem states that the total work done on an object is equal to the change in its kinetic energy. Mathematically, this can be expressed as:
$W_{t o t a l} = Δ K$
where $W_{t o t a l}$ is the total work done by all forces acting on the particle, and $Δ K$ is the change in kinetic energy.
Hint: Recall that the total work done includes contributions from both conservative and non-conservative forces.
2. Separating Work Done by Forces:
The total work done can be separated into work done by conservative forces ( $W_{c}$ ) and work done by non-conservative forces ( $W_{n c}$ ):
$W_{t o t a l} = W_{c} + W_{n c}$
Therefore, we can rewrite the work-energy theorem as:
$W_{c} + W_{n c} = Δ K$
Hint: Identify the types of forces acting on the particle and how they contribute to the work done.
3. Work Done by Conservative Forces:
For conservative forces, the work done is related to the change in potential energy ( $U$ ). The work done by conservative forces can be expressed as:
$W_{c} = - Δ U$
where $Δ U$ is the change in potential energy.
Hint: Remember that the work done by conservative forces is path-independent and depends only on the initial and final positions.
4. Combining the Equations:
Substituting the expression for $W_{c}$ into the work-energy theorem gives us:
$- Δ U + W_{n c} = Δ K$
Rearranging this, we find:
$W_{n c} = Δ K + Δ U$
Hint: This equation shows how non-conservative work relates to changes in kinetic and potential energy.
5. Conclusion:
Based on the analysis, we can conclude that:
- The work done by conservative forces is equal to the negative change in potential energy.
- The total work done includes contributions from both conservative and non-conservative forces, leading to changes in kinetic energy.
Therefore, the correct statements based on the relationships derived are:
- $W_{c} = - Δ U$
- $W_{n c} + W_{c} = Δ K$
- $W_{n c} = Δ K + Δ U$
The correct options are A, B, and C.
Final Answer:
The correct options are A, B, and C.

Updated on:7/8/2024

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Work done by the conservative force on a system is equal to :
Athe change in kinetic energy of system
Bthe change in potential energy of system
Cthe change in total machanical energy of system
DNone of the above
The negative of the work done 'by the conservative internal forces on a system equals the change in:
Atotal energy
Bkinetic energy
Cpotential energy
Dnone of these
The work done in taking a unit positive charge from P to A is $W_{A}$ and P to B is $W_{B}$ . Then
.
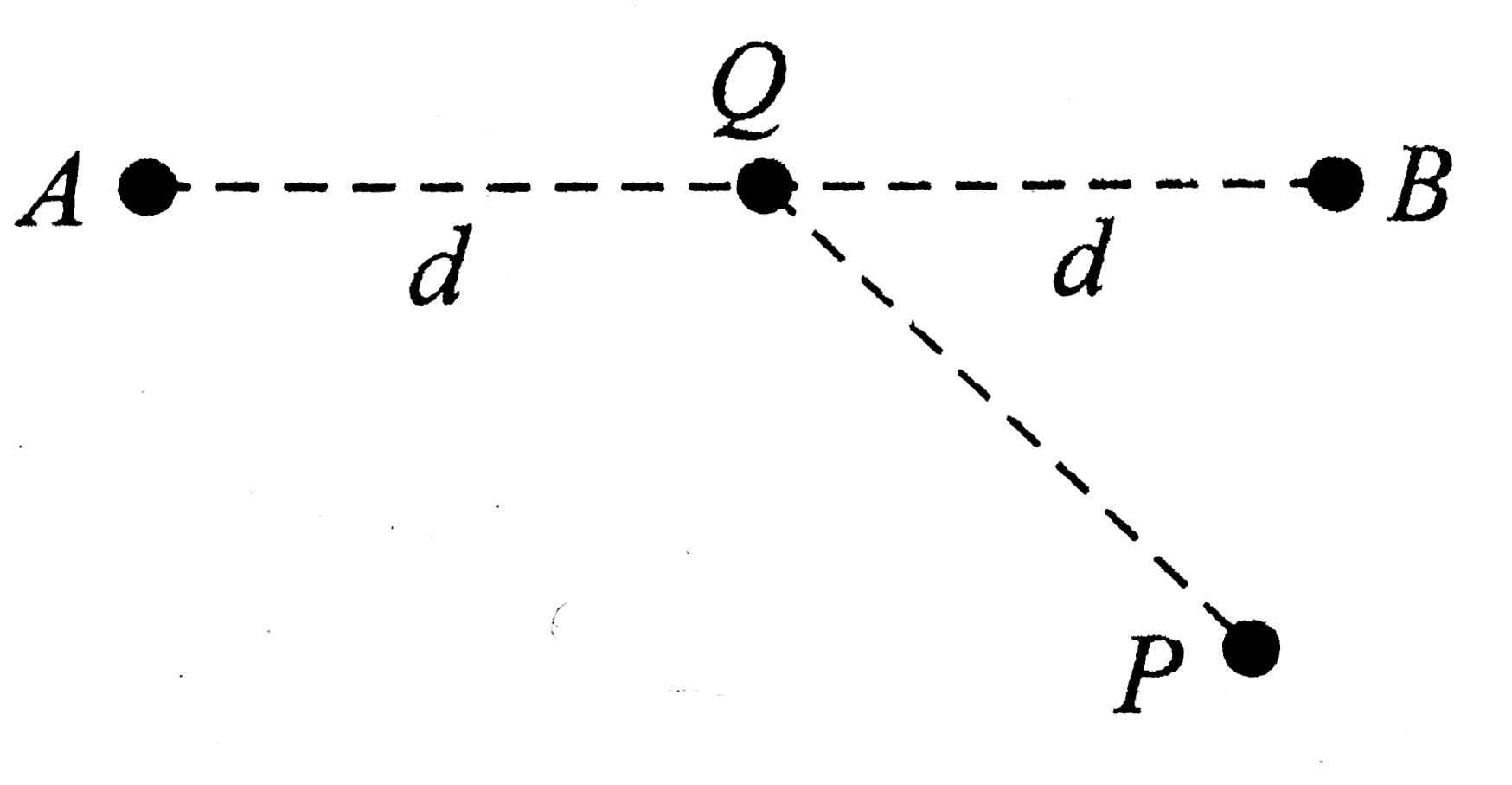A $W_{A} > W_{B}$
B $W_{A} < W_{B}$
C $W_{A} = W_{B}$
D $W_{A} + W_{B} = 0$

CENGAGE PHYSICS-WORK, POWER & ENERGY-Multiple Correct

Home
Ask Doubt
Profile