A constant force F pushes the block m till the wedge M starts sliding. If the stiffness of the light spring connecting M and m is K, coefficient of friction between block and wedge is μ1 and between the wedge and ground is μ2, find the value of the force F
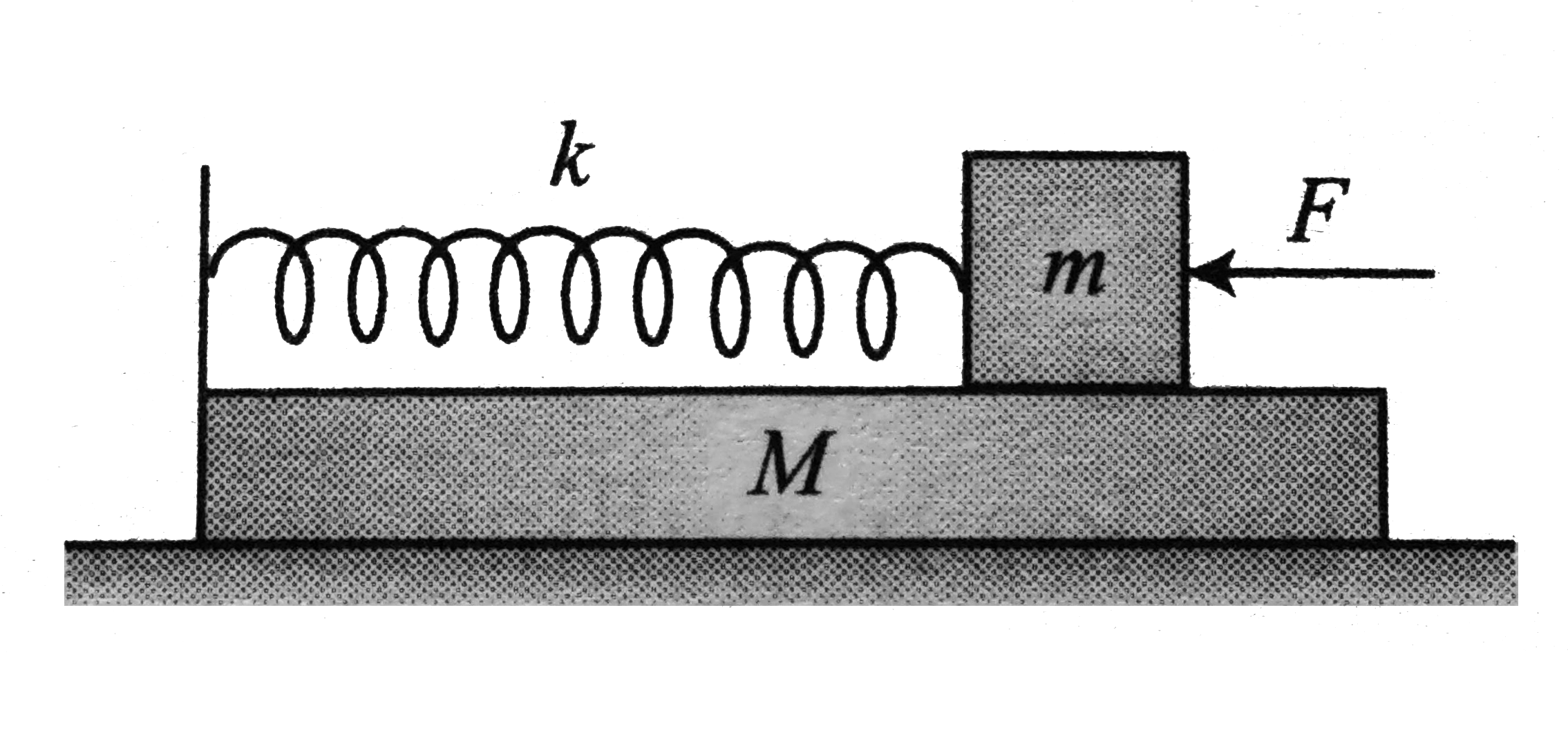
The correct Answer is:μ22(M+m)2g2−μ21m2g22k
Let x0 is the compression required so that wedge M just starts moving.

μ1mg+kx0=μ2(M+m)g
⇒x0=μ2(M+m)g−μ1mgk
Now for block: Wtotal=Δk=k2−k1
⇒Fx0−μ1mgx0−12kx20=0
⇒WF=Fx0=μ1mgx0+kx202
⇒WF=(μ1mg+kx02)x0=μ22(M+m)2g2−μ21m2g22k
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Single Correct
Explore 100 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.5
Explore 15 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
The coefficient of friction between the block and the wedge is μ. Friction between the wedge and the table is to be neglected.
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View Solution
Knowledge Check
A block of mass m2 is placed on a horizontal table and another block of mass m1 is placed on top is it. An increasing horizontal force F=αt is exerted on the upper block but the lowwer block never moves as a result. If the coefficient of friction between the blocks is μ1 coefficient of friction between the blocks is μ1 and that between the lower block and the table is μ2, then what is the maximum possible value of μ1/μ2 ?
Am2m1B1+m2m1Cm1m2D1+m1m2Calculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
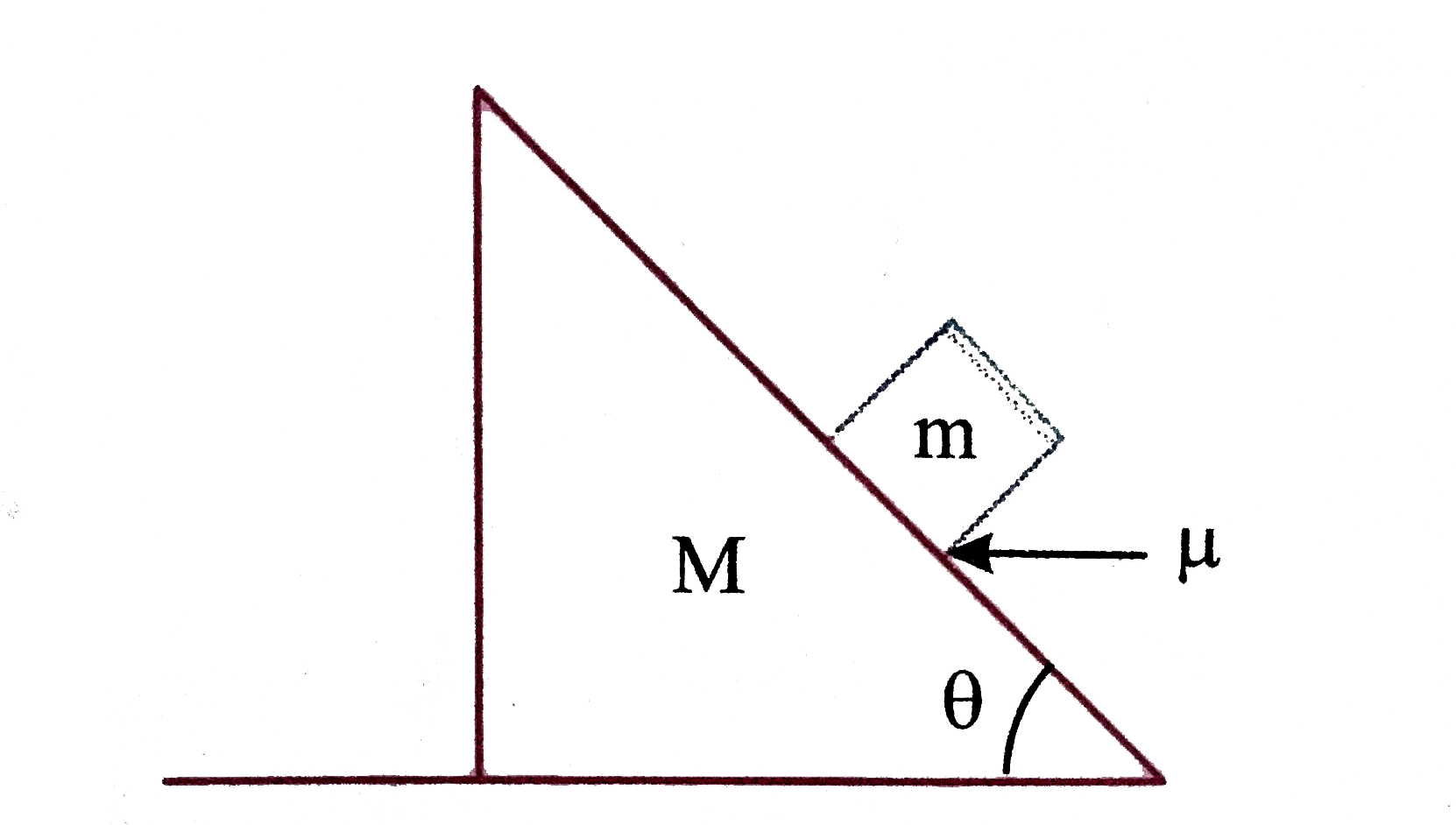 Atan−1μB2θCθDθ2
Atan−1μB2θCθDθ2a Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
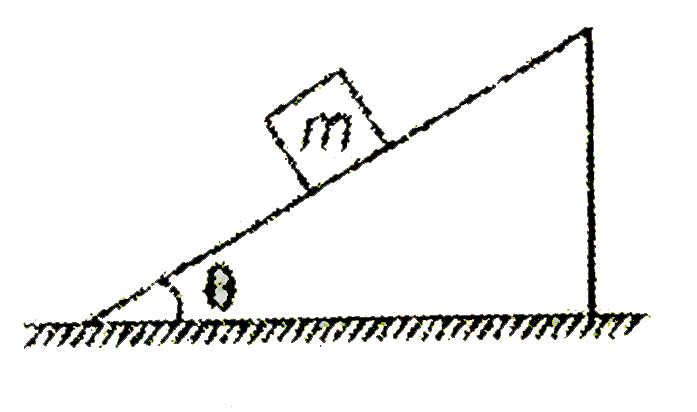 Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
The coefficient of friction between the wedge and the table is μ. Friction between the block and the wedge is to be neglected.
View SolutionBlock A of mass m and block B of mass 2m are placed on a fixed triangular wedge by means of a light and inextensible string and a frictionless pulley as shown in fig . The wedge is inclined at 45∘ to the horizontal on both sides . The coefficient of friction between the block Aand the wedge is 2/3 and that between the block B and the wedge is 1/3 .If the system of AandB is released from rest then find .
a. the acceleration of A
b. tension in the string
c.the magnitude and direction of the frictional force acting on A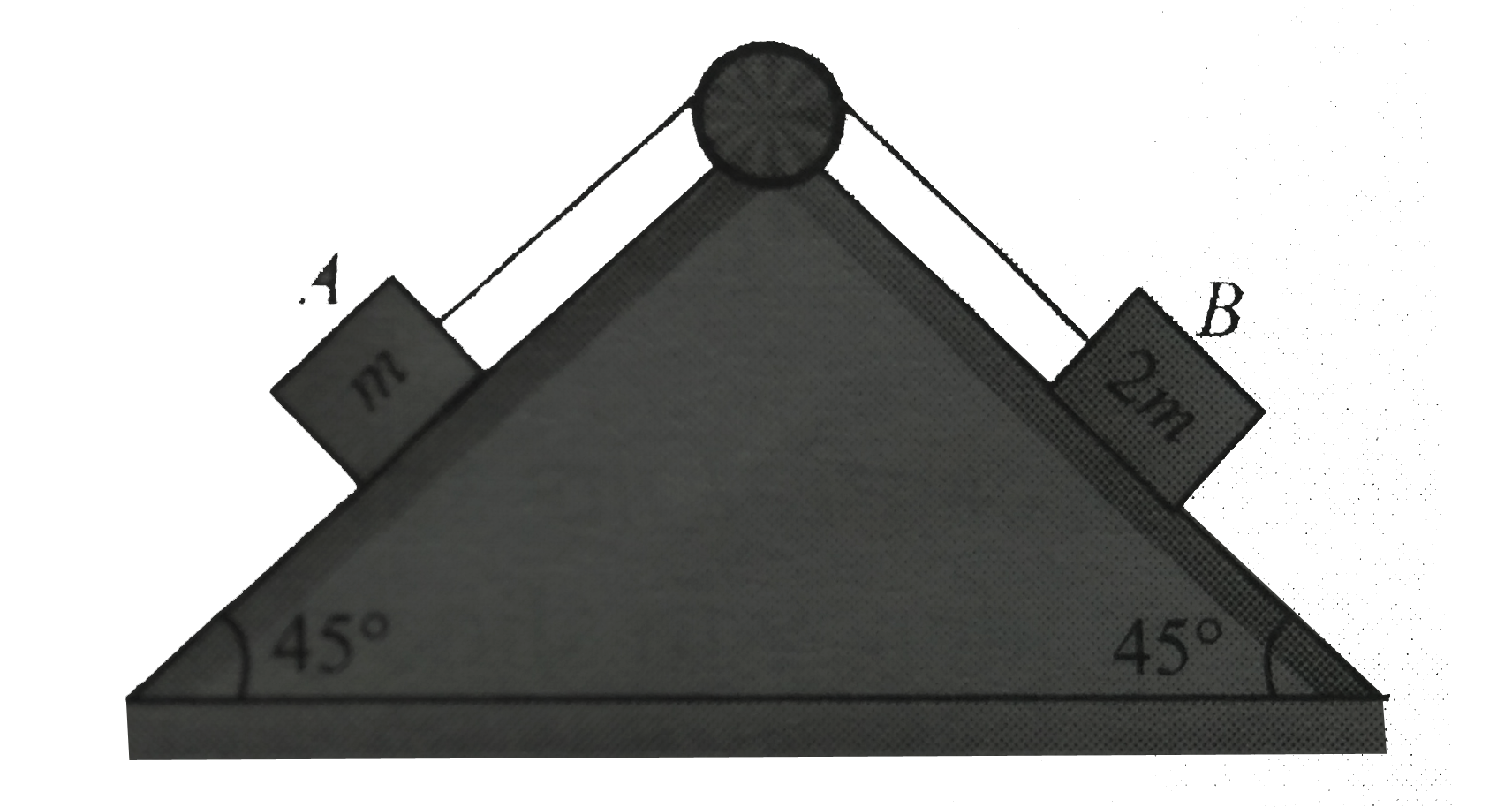
View SolutionIn the figure shown coefficient of friction between block A and ground is 0.4 and that between wedge and block B is zero. Wedge is fixed. Find tension is string and acceleration of block A if F = 28 N.

View SolutionIn the figure shown the pulley is smooth . The spring and the string are light. The block 'B' slides down from the top along the fixed rought wedge of inclination θ. Assuming that the block reaches the end of the wedge. Find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and the spring was relaxed when the block was relased from the top of the wedge.
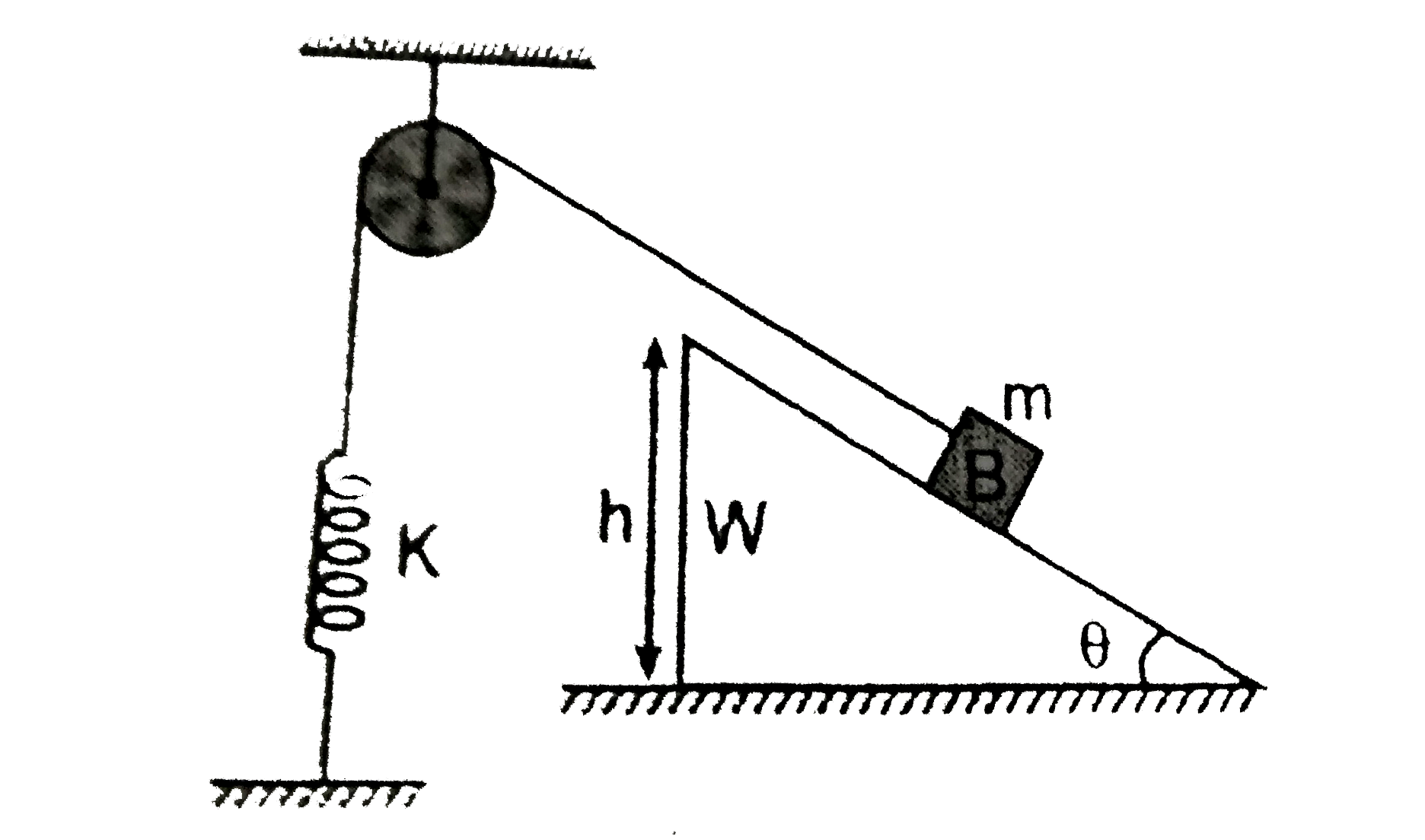
View SolutionIn figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.
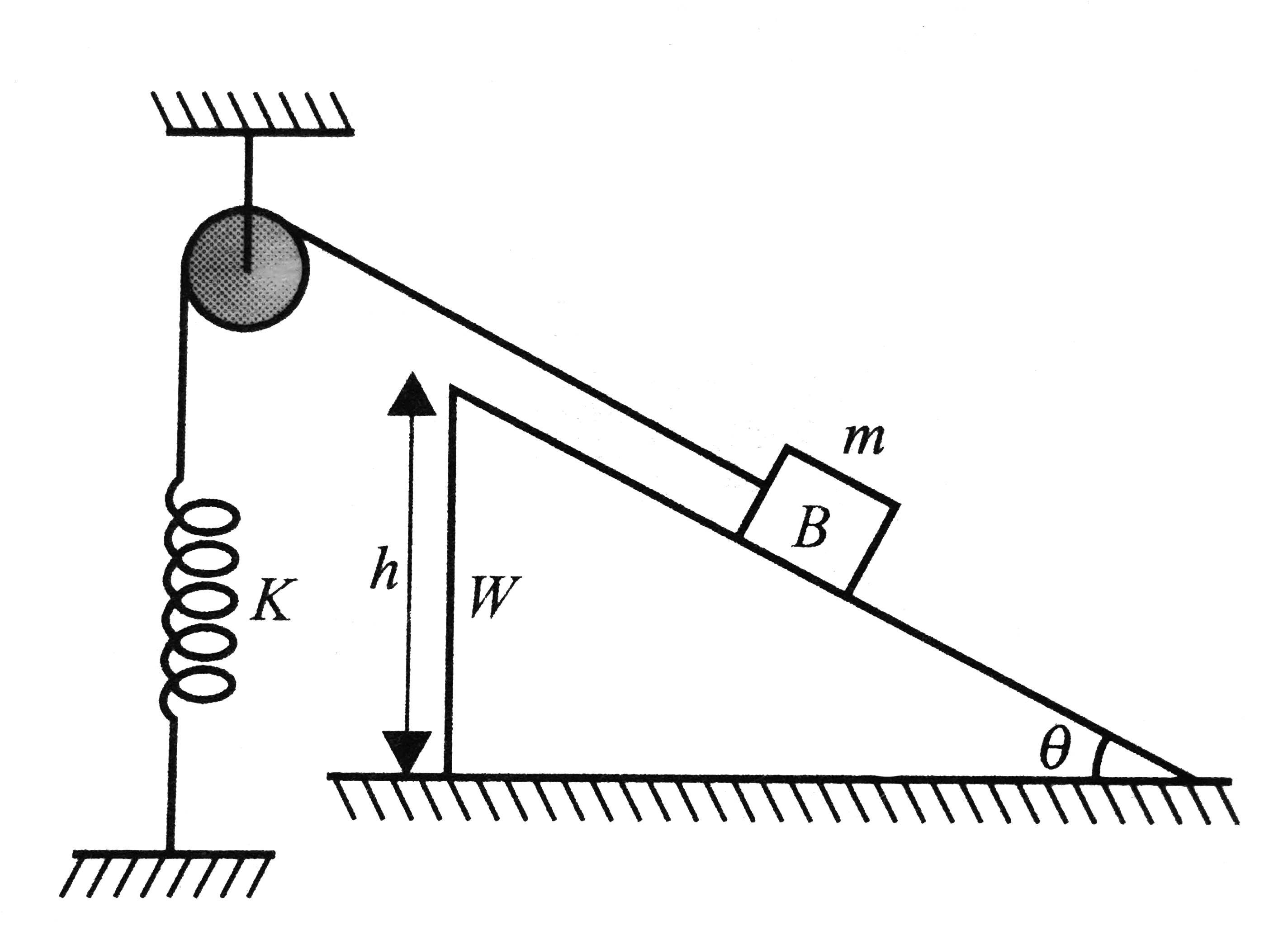
View Solution

