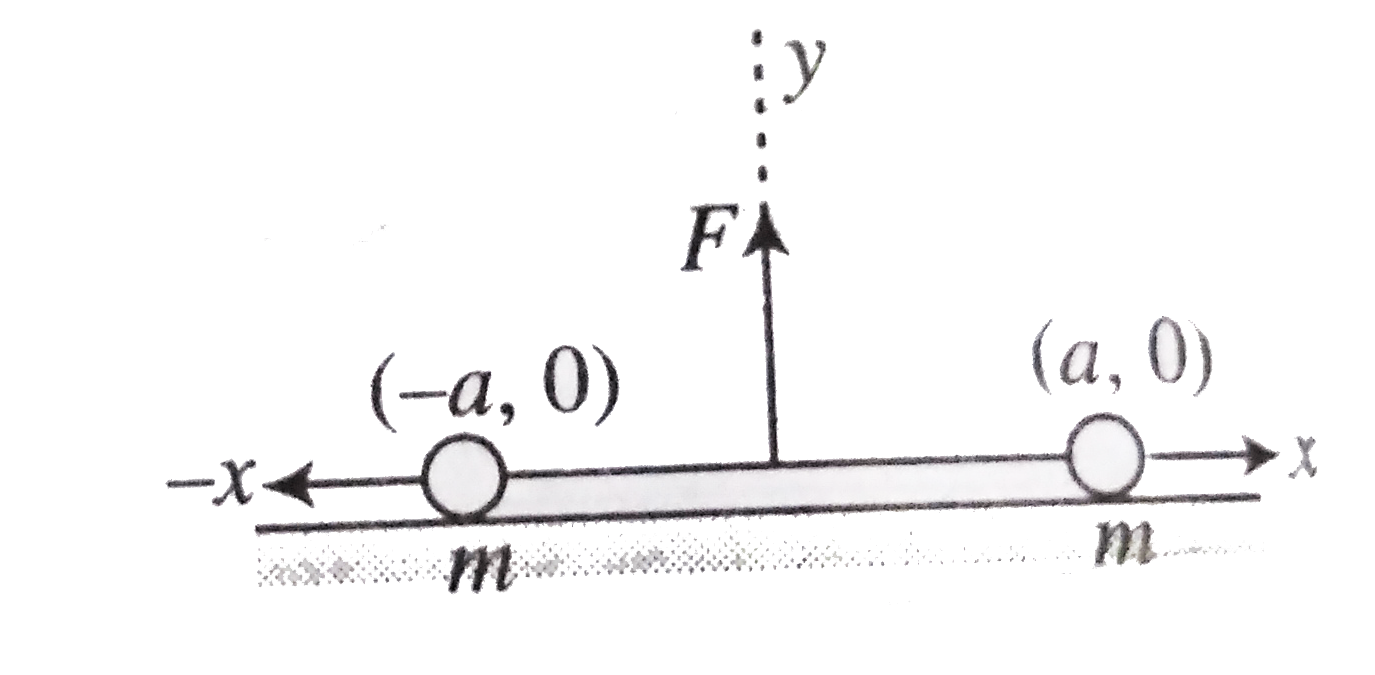
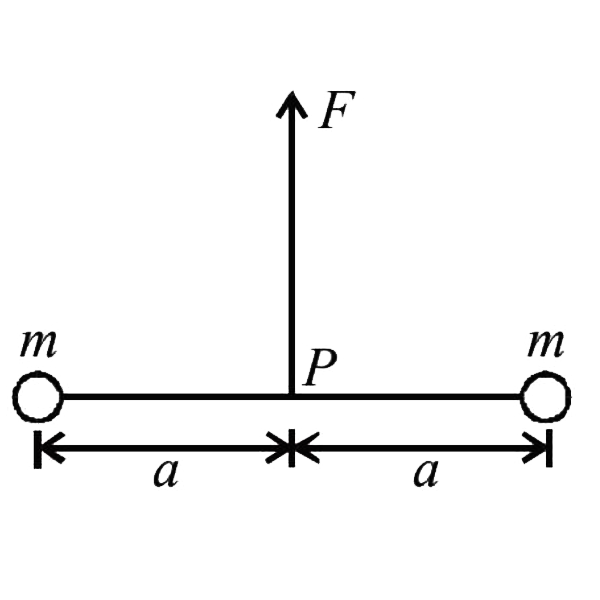
Two masses each equal to m are lying on x-axis at (−a,0)(+a,0) respectively as shown in figure They are connected by a light string A force F is applied at the origin along vertical direction As a result the masses move toward each other without loosing contact with ground What is the acceleration of each mass? Assume the instantanceous position of the masses as(−x,0)and (x,0)
2Fm√a2−x2x
2Fm.x√a2−x2
F2m.x√a2−x2
Fmx√a2−x2
The correct Answer is:c
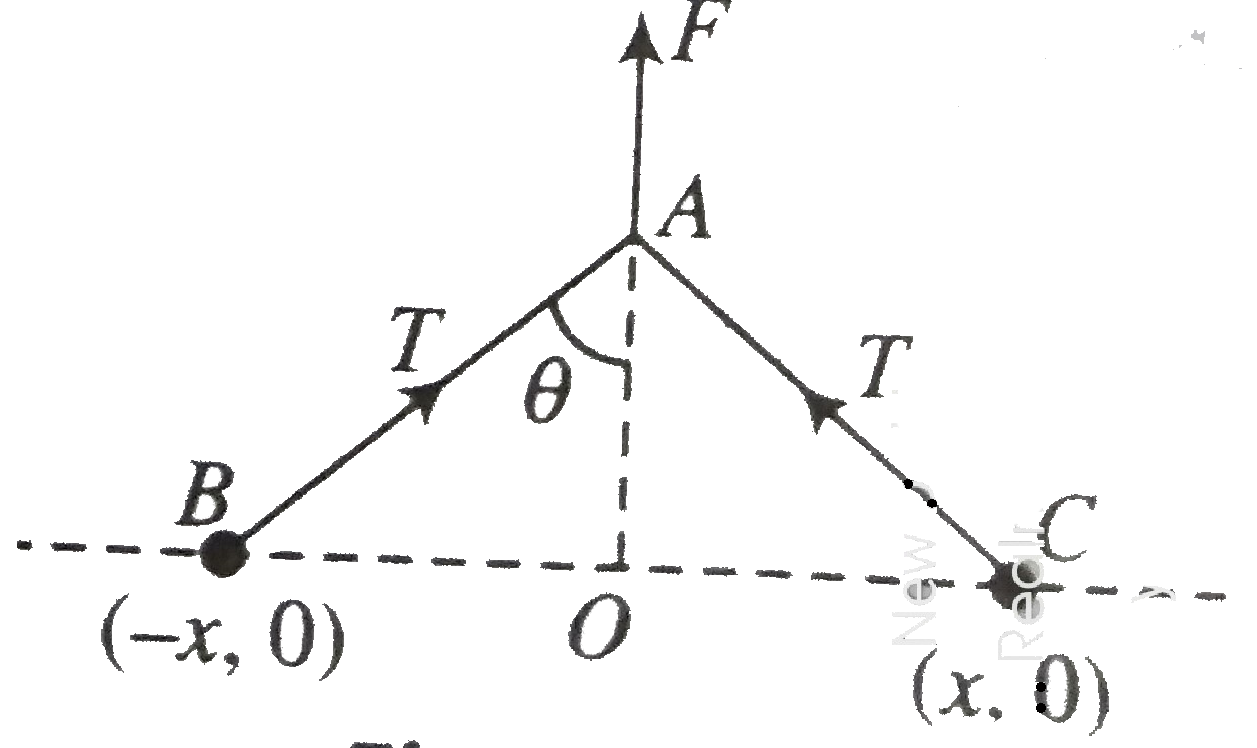
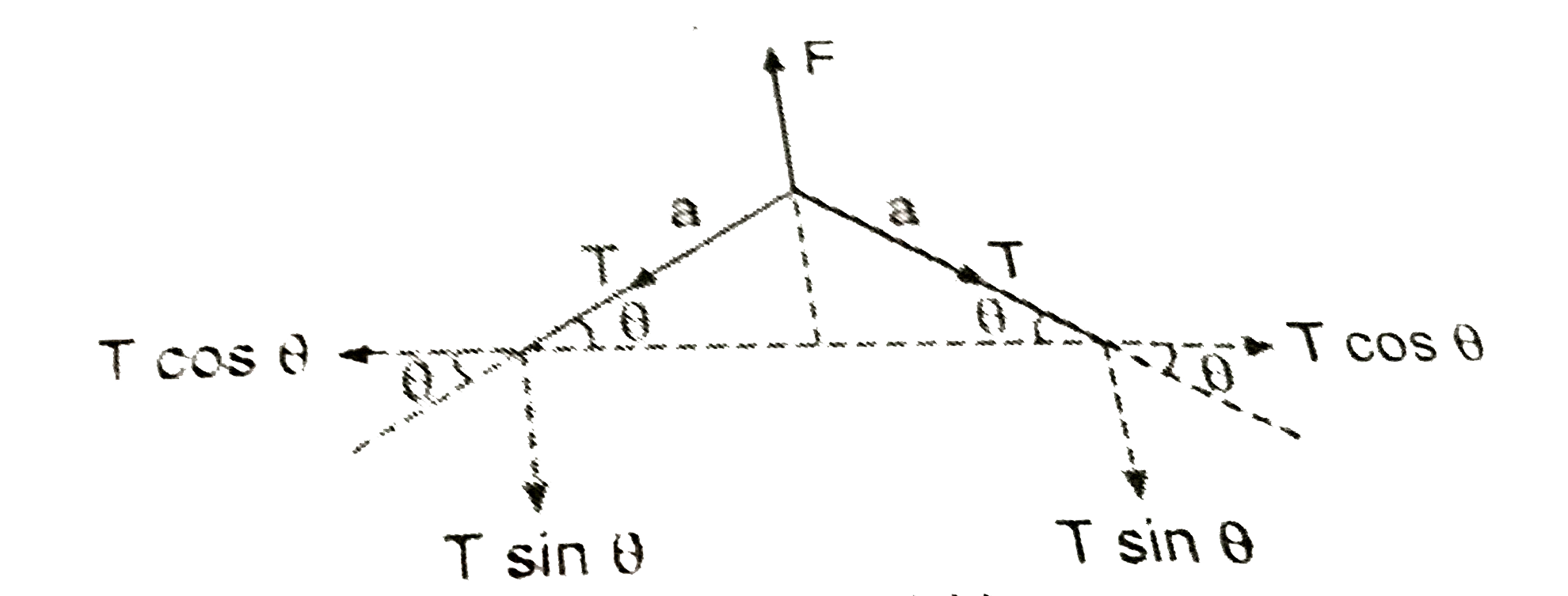
From figure F=2Tcosθ
T=F/2cosθ
The force responsible for motion of masses m x-axis is Tsinθ
ma=Tsinθ=F2sinθ×sinθ
=F2tanθ=F2×OBOA=F2×x√(a2−x2)
So a=F2m=x√a2−x2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Multiple correct answer type
Explore 3 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Assertion -reasoning
Explore 2 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:True And False
Explore 4 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
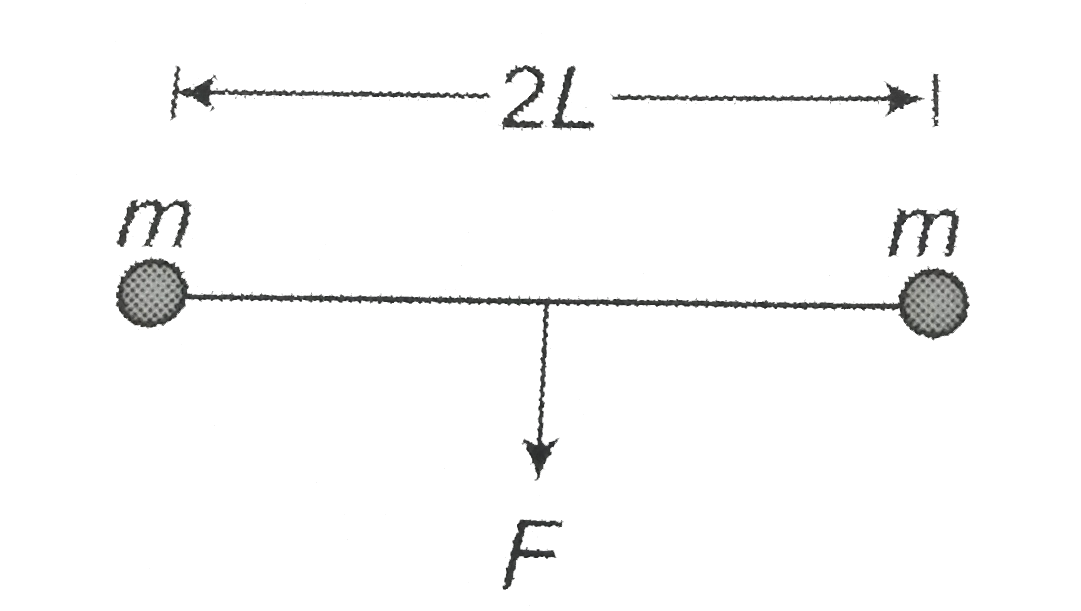
Two particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
View SolutionTwo point masses, each of mass 'm' are connected to the end of spring. If force F is applied on one of the mass, then find the acceleration of this mass if the acceleration of other mass is a ?
View Solution
Knowledge Check
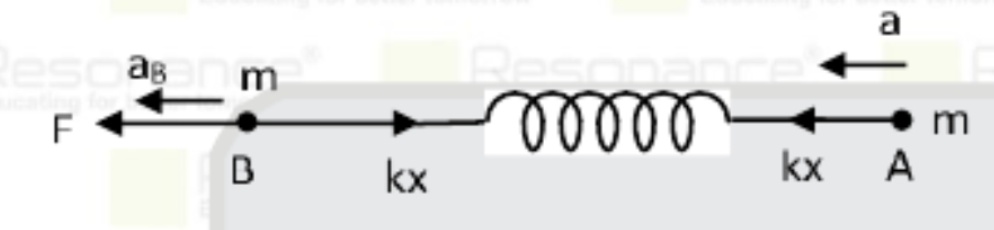
Two bodies A and B each of mass M are fixed together by a massless spring A force F acts on the mass B as shown in fig At the instant shown the mass A has acceleration a. What is the acceleration of mass B?
 A(F/M)−aBaC−aD(F/M)
A(F/M)−aBaC−aD(F/M)Two particles of mass 'm' each are tied at eh ends of a light string of length '2a' The whole system is kept on frictionless horizontal surface with the string held tight so that each mass is at a distance 'a' from the centre P (as shown in figure). Now the mid point of the string is pulled vertically upwards with a small but constant force F As a result, the particles move towards each other on the surface the magnitude of acceleration, when the separation between them becomes 2x is:
 AF2ma√a2−x2BF2mx√a2−x2CF2mxaDF2m√a2−x2x
AF2ma√a2−x2BF2mx√a2−x2CF2mxaDF2m√a2−x2xTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
 AF2m/(√a2−x2)BF2mx√a2−x2CF2mxaDF2m√a2−x2x
AF2m/(√a2−x2)BF2mx√a2−x2CF2mxaDF2m√a2−x2x
A horizontal force F=2N is applied on the system shown in the figure.All surfaces are smooth.All pulleys and string are ideal.Mass of A and B each is 1 kg.What is the acceleration of B with respect to A
View SolutionTwo particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x

View SolutionTwo blocks are attached by a light inextensible string and the system is pulled by applying a force F0 as shown in the diagram. Find the acceleration of each block and tension in the string.

View SolutionTwo blocks of masses m and M are placed on a horizontal frictionless table connected by light spring as shown in figure. The Mass M is pulled to the right with a force F It the acceleration of mass m is a then the acceleration of M will be .

View SolutionThree blocks with masses m , 2m and 3m are connected by strings, as shown in the figure. After an upward force F is applied on block m , the masses move upward at costant speed v . What is the net force on the block of mass 2m ? (g is the acceleration due to gravity). ltBrgt

View Solution

