Two smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.

m'm+Mg
m'mg
m'Mg
mm'g
The correct Answer is:b
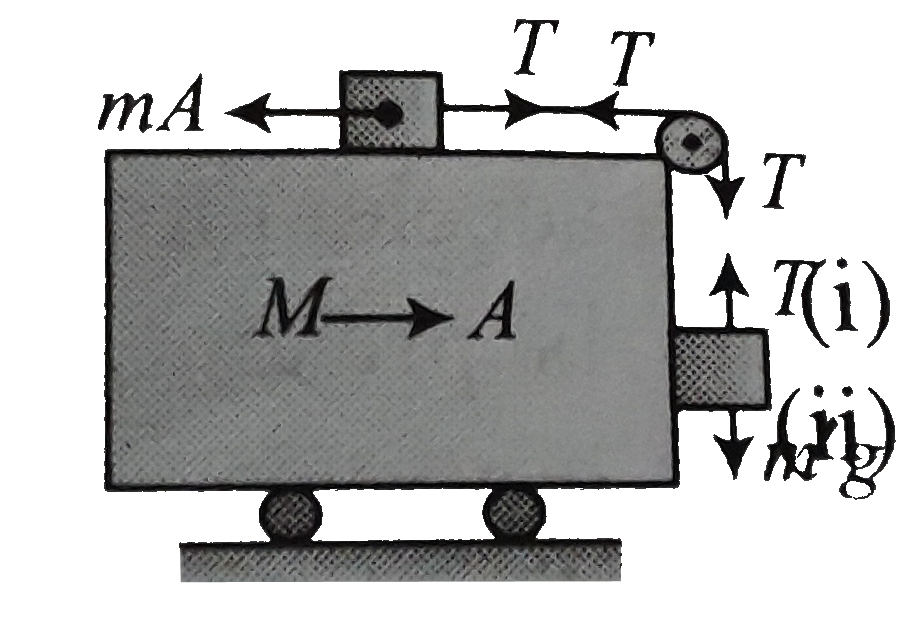
FBD The force acting on the block m and m' to the surface in contact are given an mA←,T→mg↓andT↑force equation relative to M Since amM=a1=0
For m−Ma+T=0
ForM:T−m'g=0
FromEqs(i) and (ii) A=m'mg
b. Force equation on M+m+m'
∑Fx=max
F=MA+mA+m'A=(M+m+m')A
=(M+m+m')m'mg
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer
Explore 6 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:True And False
Explore 4 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Multiple Correct
Explore 2 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Two blocks of masses m1 = 3 kg and m2=1√3 kg are connected by a light inextensible string which passes over a smooth peg . The blocks rest on the inclined smooth planes of a wedge and the peg is fixed to the top of the wedge . The planes of the wedge supporting m1 and m2 are inclined at 30∘ and 60∘ respectively , with the horizontal. Calculate the acceleration of masses and the tension in the string .
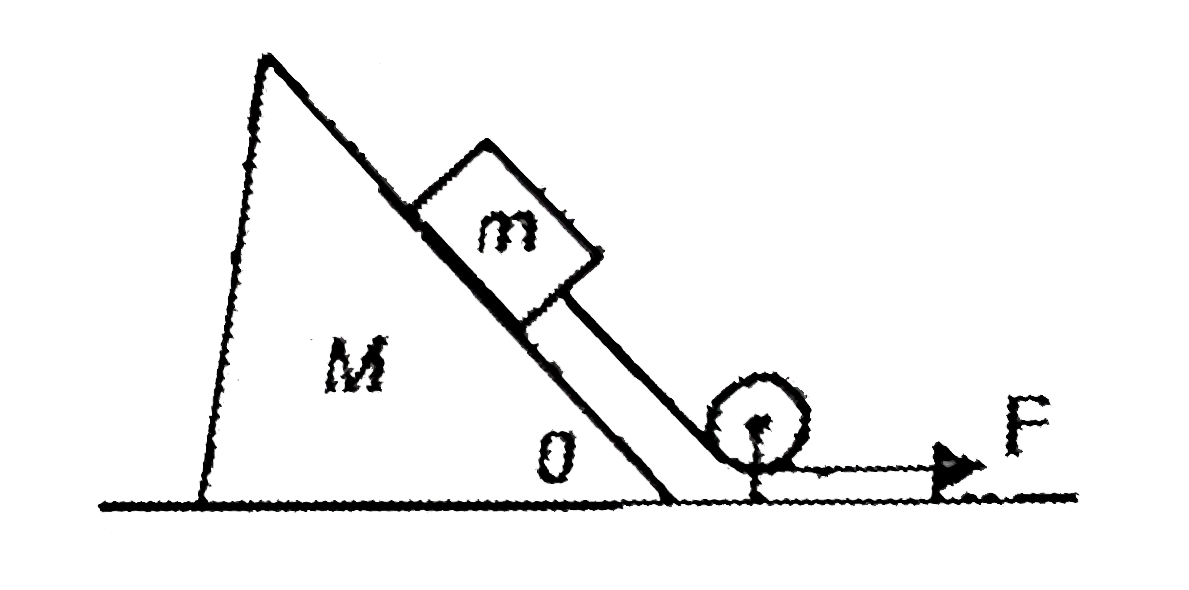
View SolutionIn the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
View Solution
Knowledge Check
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θAll surfaces are smooth. The acceleration of mass m relative to the wedge is
 AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
AgsinθBgsinθ+acosθCgsinθ−acosθDacosθA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
A(M+m)gB(M+msinθ)gCMgD(M+msinθM+m)gcosθ
A block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.

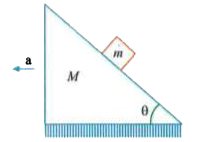
View SolutionA block of mass m is placed on a smooth wedge of inclination. The whole system is accelerated horizontally so that block does not slip on the wedge Find the i) Acceleration of the wedge Force to be applied on the wedge Force exerted by the wedge on the block .
View SolutionAll surfaces are smooth The acceleration of mass m relative to the wedge is
 .
.
View SolutionA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.

View SolutionThe minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
View Solution

