An inextensible string AB is tied to a block B of negligible dimensions and passes over a small pulley C so that free end A hangs h unit above the ground on which the block B rests. In this initial position shown in fig. The free end A is h unit below C. if now end A moves horizontally with a velocity v0, obtain an expression for the velocity of the block at any time t.

In time t, the end A moves to the position A1 so that distance AA1=v0t. The block B moves upwards to the position B1. Let BB1=y.
Then length A1C=h+y
In the ΔACA1,A1C2=AC2+AA2
(h+y)2=h2+(v0t)2
or h2+y2+2hy=h2+v20t2
or y2+2hy−v20t2=0
After solving eq. (i) we get
y=−h+√h2+v20t2
This is the equation for the displacement y of the block.
For velocity of the block differentiating equation (i) w.r.t. time
v=dydt=ddt[−h+(h2+v20t2)1/2]
=12(h2+v20t2)−1/2×2v20t
=v0t(h2+v20t2)1/2.

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.4
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.2
Explore 35 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
In the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.

View SolutionTwo identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving
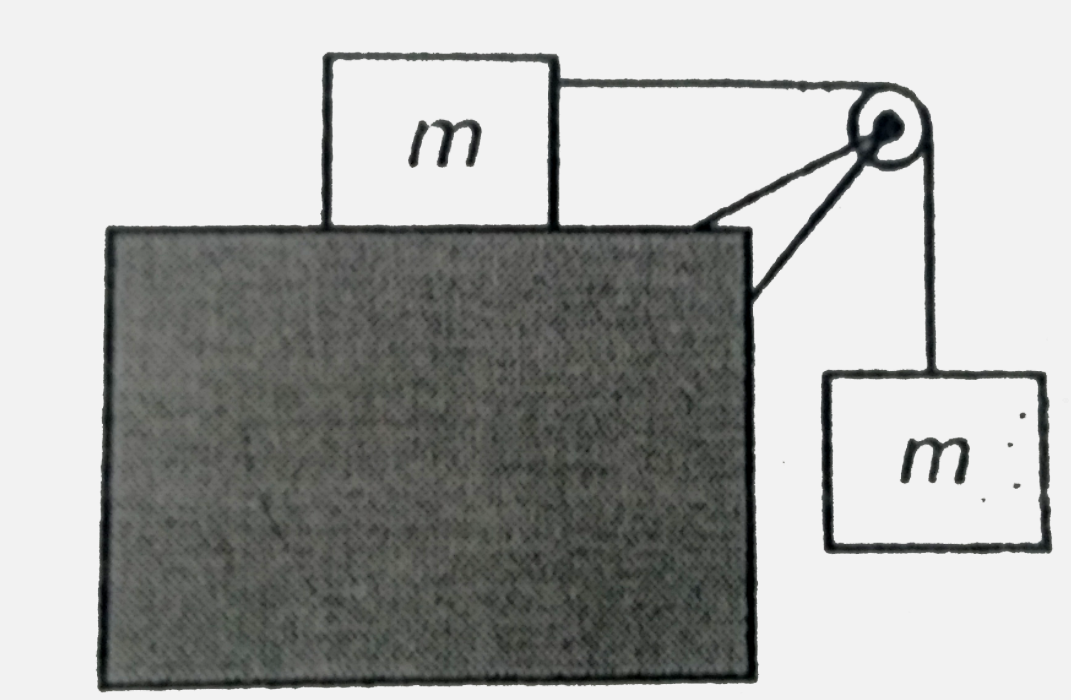
View Solution
Knowledge Check
If block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
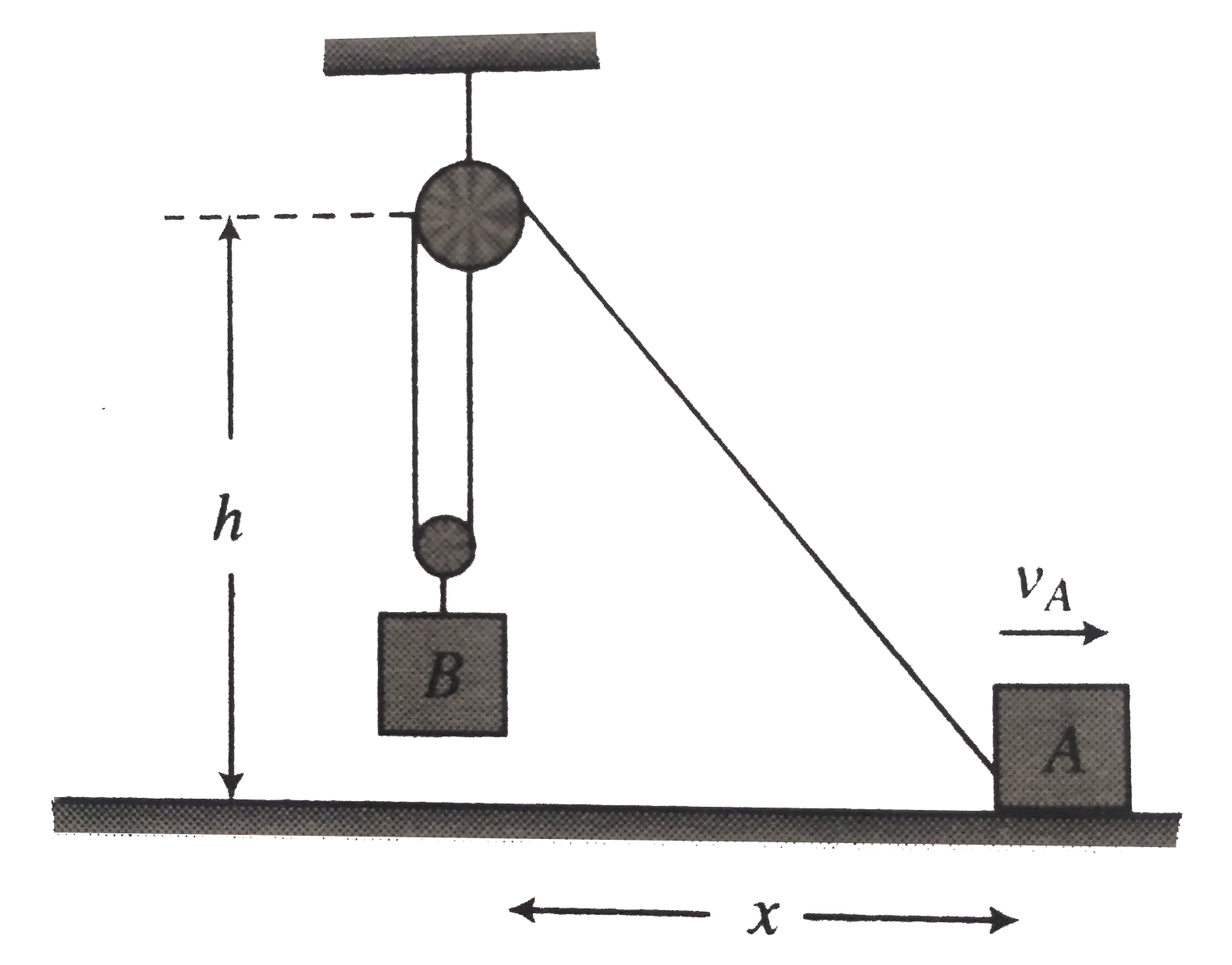 AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2A block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :
 AvBvsinθCv//sin thetaDv/cosθ
AvBvsinθCv//sin thetaDv/cosθIn the arrangement shown, end A of light intextensible string is pulled with constant velocity v. the velocity of block B is
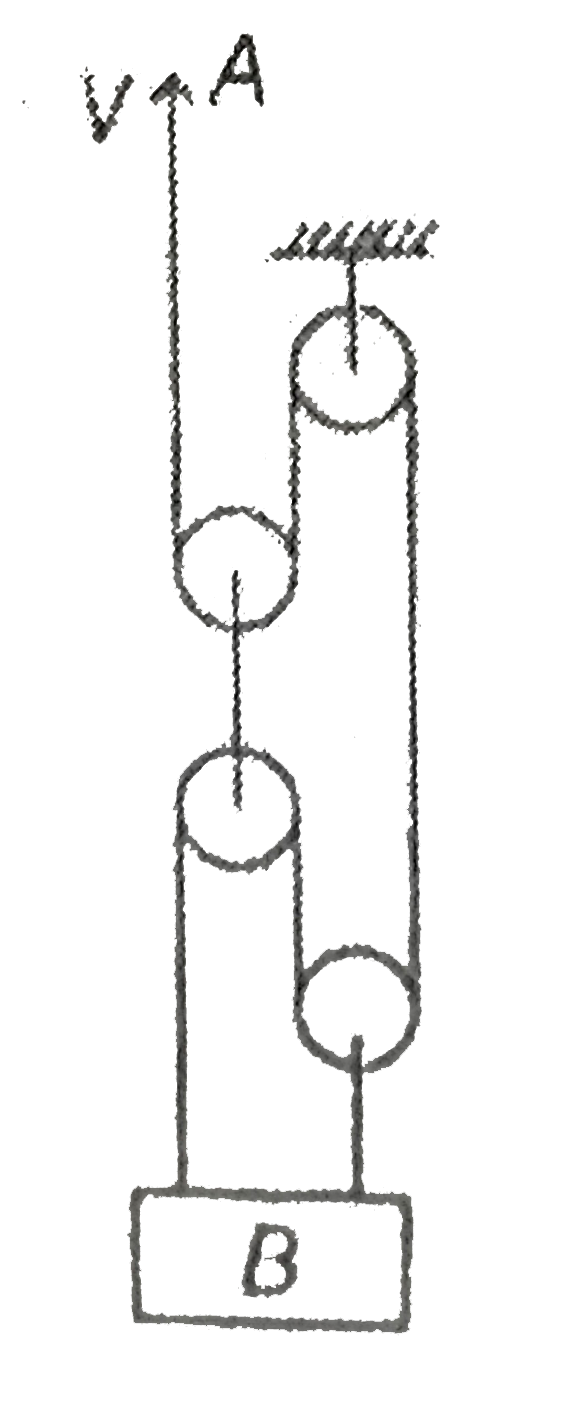 AV/2BvCv/3D3v
AV/2BvCv/3D3v
The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View Solution
Two blocks are connected by an inextensible string as shown. The pulley is fixed. If block A moves down with speed v, find the velocit of block B at instant.
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
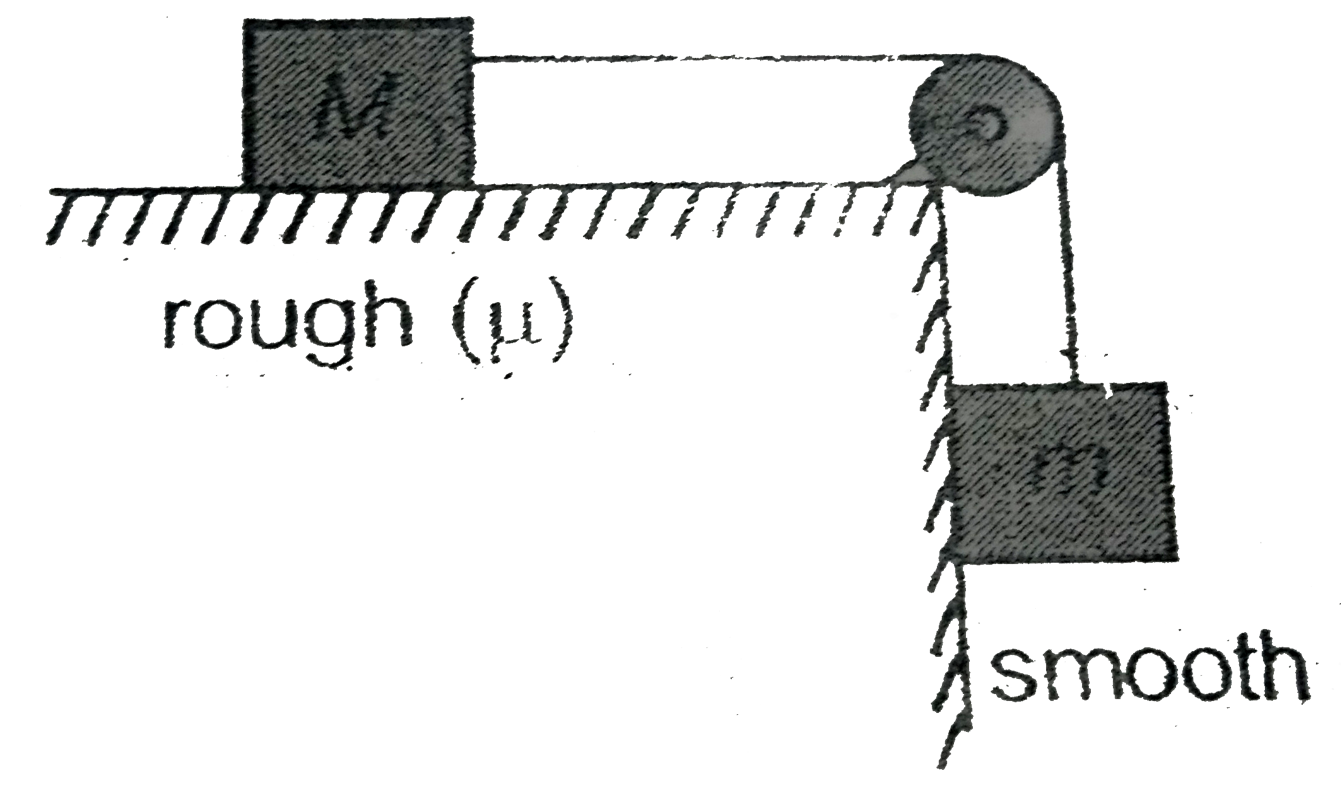
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
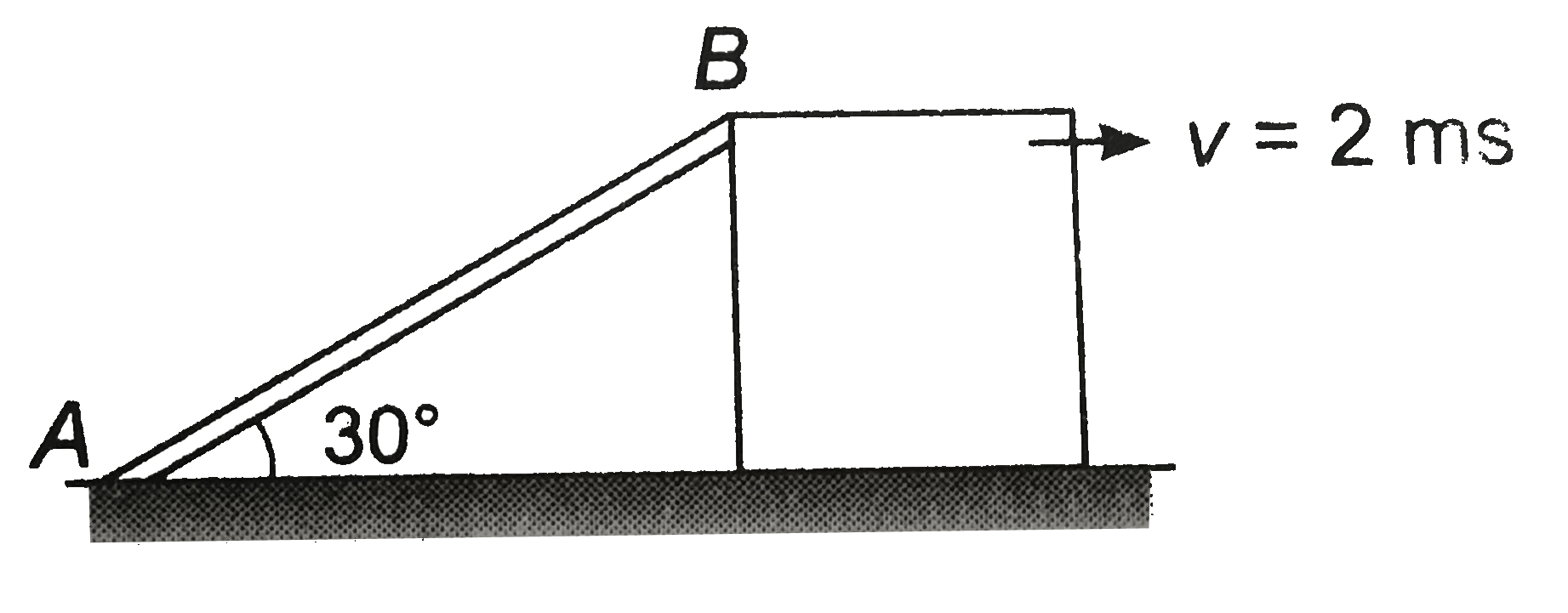
View Solution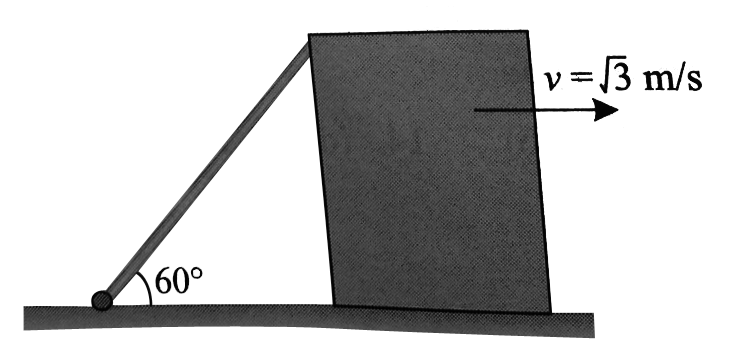
A rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity m/s towards right. The velocity of end B of rod when rod makes an angle of 60∘ with ground is :
View Solution

