Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity u. As a result of this, end A starts moving down along the wall. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

Let us first find the relation between the two displacements. Then differentiate with respect to time. Here if the distance from the corner to the point A is x and that up to B is y, the left velocity of pointA can be given as vA=(dx)/(dt) and that of B can be given as vB=−(dy)/(dt) (negative sign indicates y decreasing).
If we relate x and y: x2+y2=l2
Differentiating with respect to t, 2xdxdt+2ydydt=0
⇒xvA=yvB=xu=yvB⇒vB=uxy=ucotθ
Alternatively: In cases where distance between two points is always fixed, we can say the relative velocity of one point of an object with respect to any other point of the same object in the direction of the lime joining them will always remain zero, as their separation always remains constant.
Here, in the above example, the distance between the points A and B of the rod always remains constant, thus, the two points must have the same velocity components in the direction of their line joining, i.e., along the length of the rod.
If point B is moving down with velocity vB its component along the length of the rod is vBsinθ. Similarly the voelcity components of point A along the length of rod is ucosθ. Thus, we have vBsinθ=ucosθ or vB=ucotθ.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Solved Examples
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.1
Explore 11 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View Solution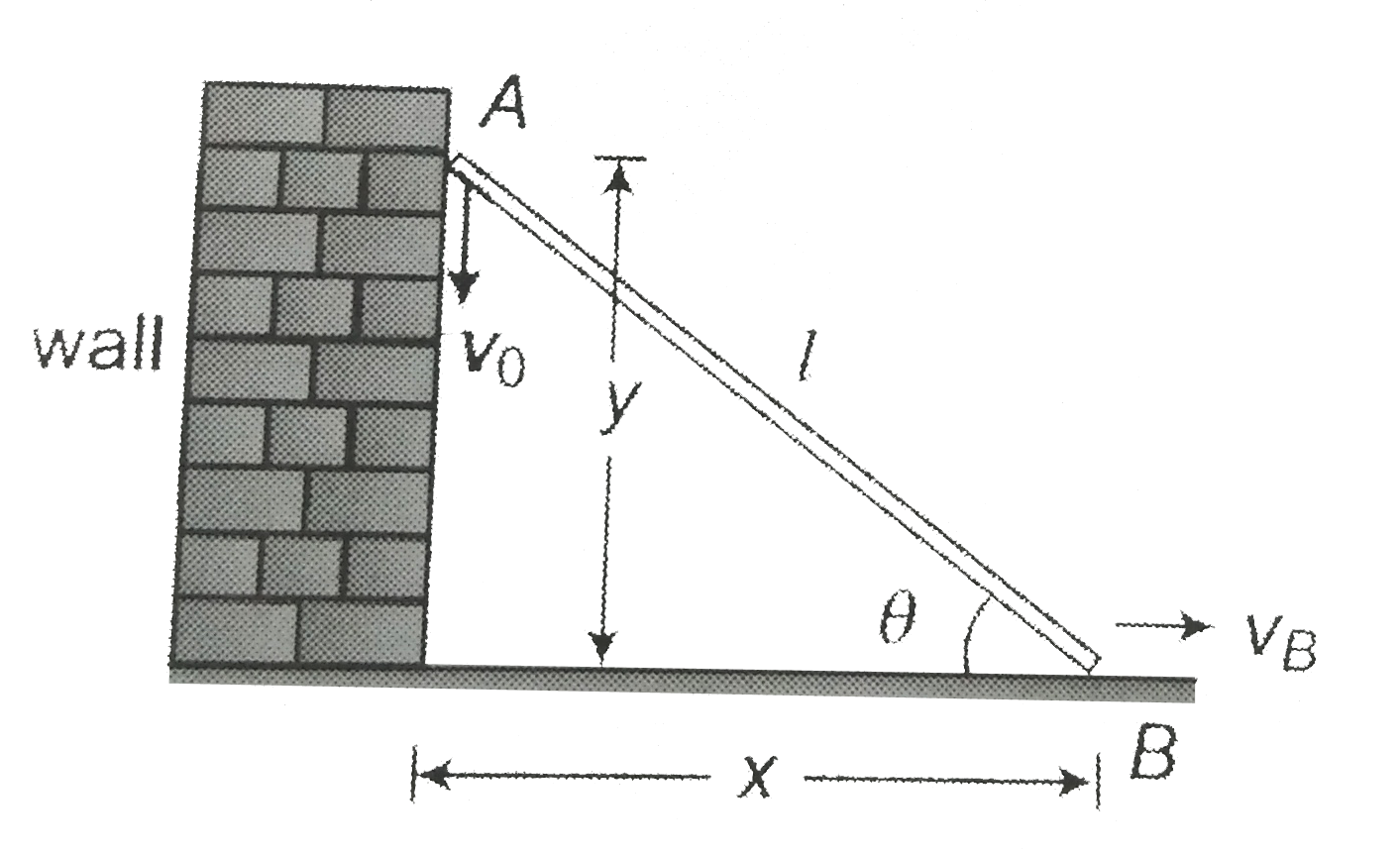
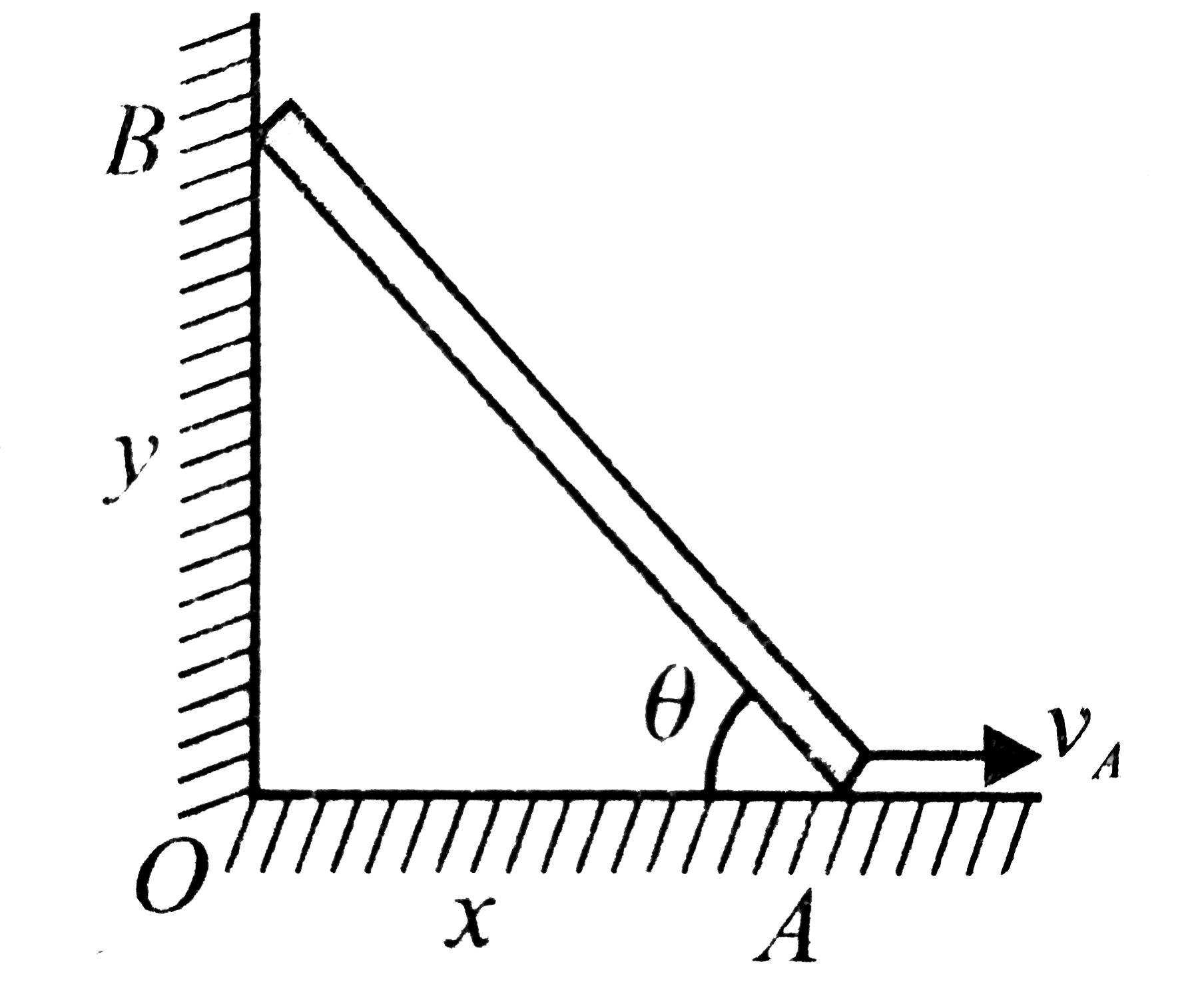
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View Solution
Knowledge Check
End A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate
the velocity of the CM of the rodA57v0 at tan−143 below horizontalB57v0 at tan−134 below horizontalC56v0 at tan−134 below horizontalD56v0 at tan−143 below horizontal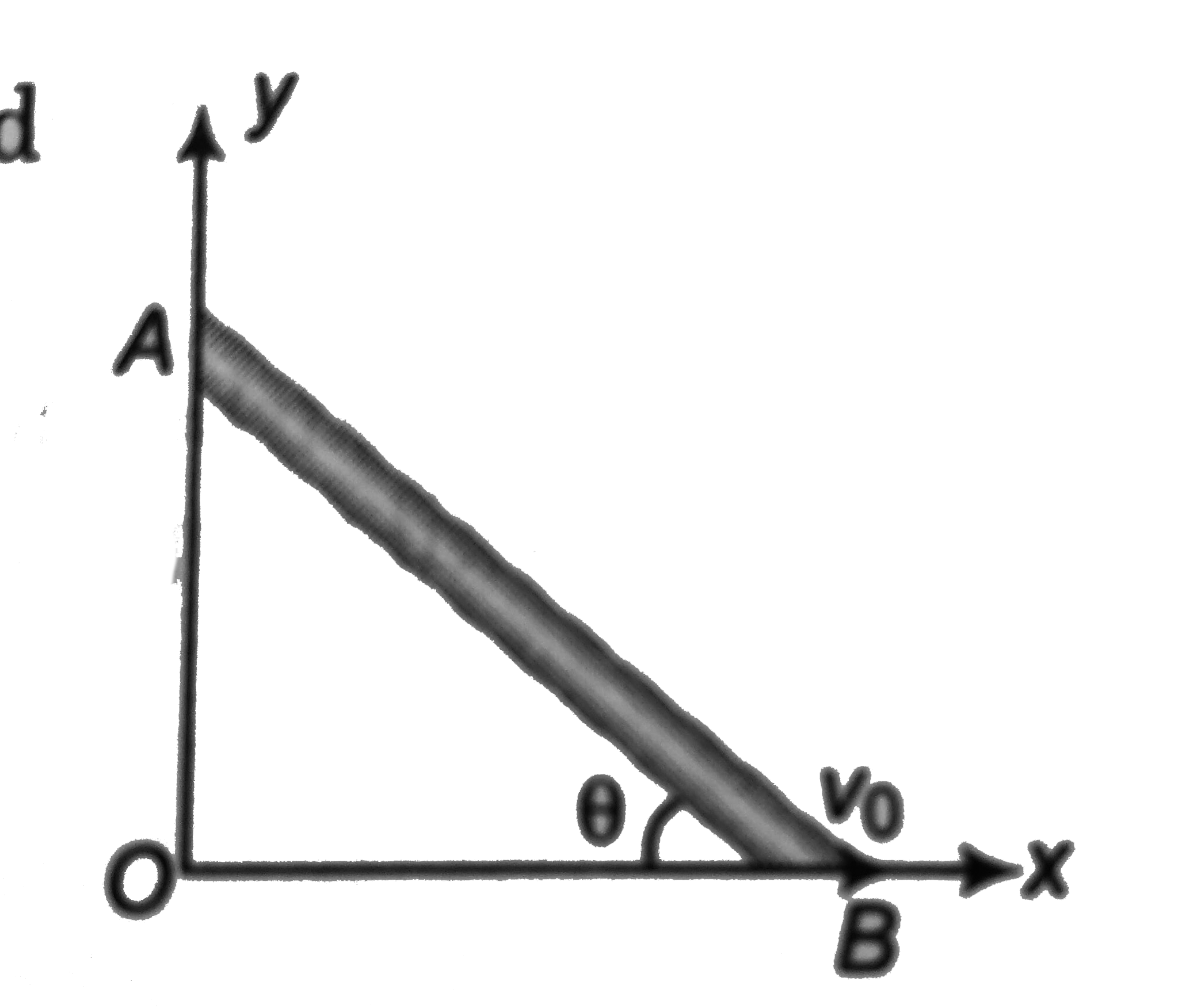
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.AAt θ=37∘ velocity of end A is 43v0 downwardsBAt θ=37∘ angular velocity of rod is 5v03lCAngular velocity of rod is constantDvelocity of end A is constant.A rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.
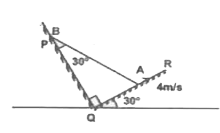 A8m/sB2√3m/sC4√3m/sD4√3m/s
A8m/sB2√3m/sC4√3m/sD4√3m/s
A uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA rod of length 'l' is inclined at an angle 'theta' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1 what is the velocity of end B at the instant when rod makes 'theta' angle with the horizontal .
View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.
View Solution

