Two forces of unequal magnitude simultaneously act on a particle making an angle $θ (= 120^{\circ})$ with each other.If one of them is reversed ,the accelaration of the particle is become $\sqrt{3}$ times. Calculate the ratio of the magnitude of the forces.

Video Solution

Text Solution

Verified by Experts

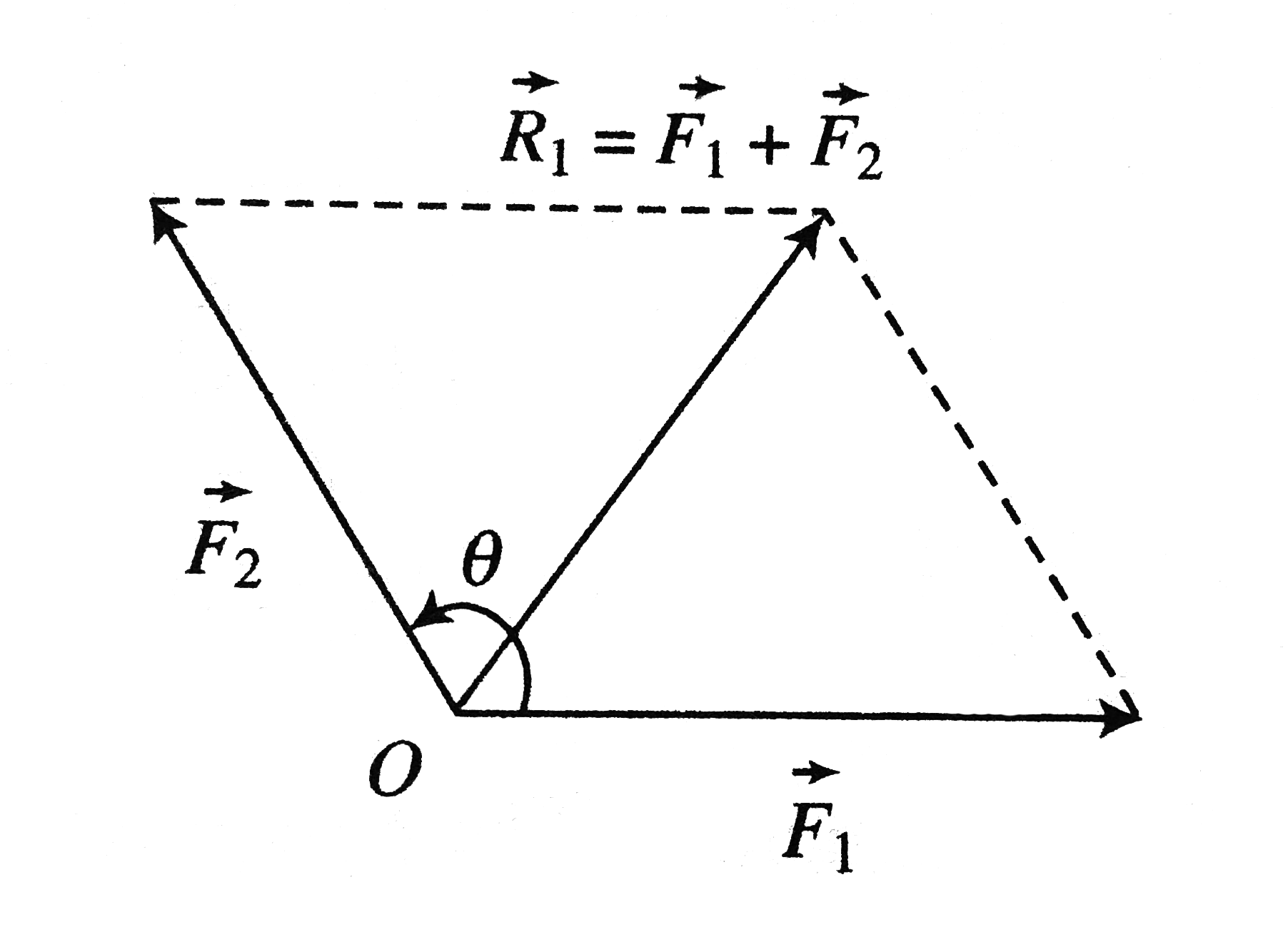
Let the two forces be ${\to F}_{1}$ and ${\to F}_{2}$ that are inclined at angle $θ$ .
.
The resultant of these forces is ${\to R}_{1} = {\to F}_{1} + {\to F}_{2}$ . Then $∣ ∣ {\to R}_{1} ∣ ∣ = ∣ ∣ {\to F}_{1} + {\to F}_{2} ∣ ∣$ .
Using parallelogram law of vector addition,we have
$∣ ∣ {\to R}_{1} ∣ ∣ = \sqrt{F_{1}^{2} + F_{2}^{2} + 2 F_{1} F_{2} cos θ}$ ....(i)
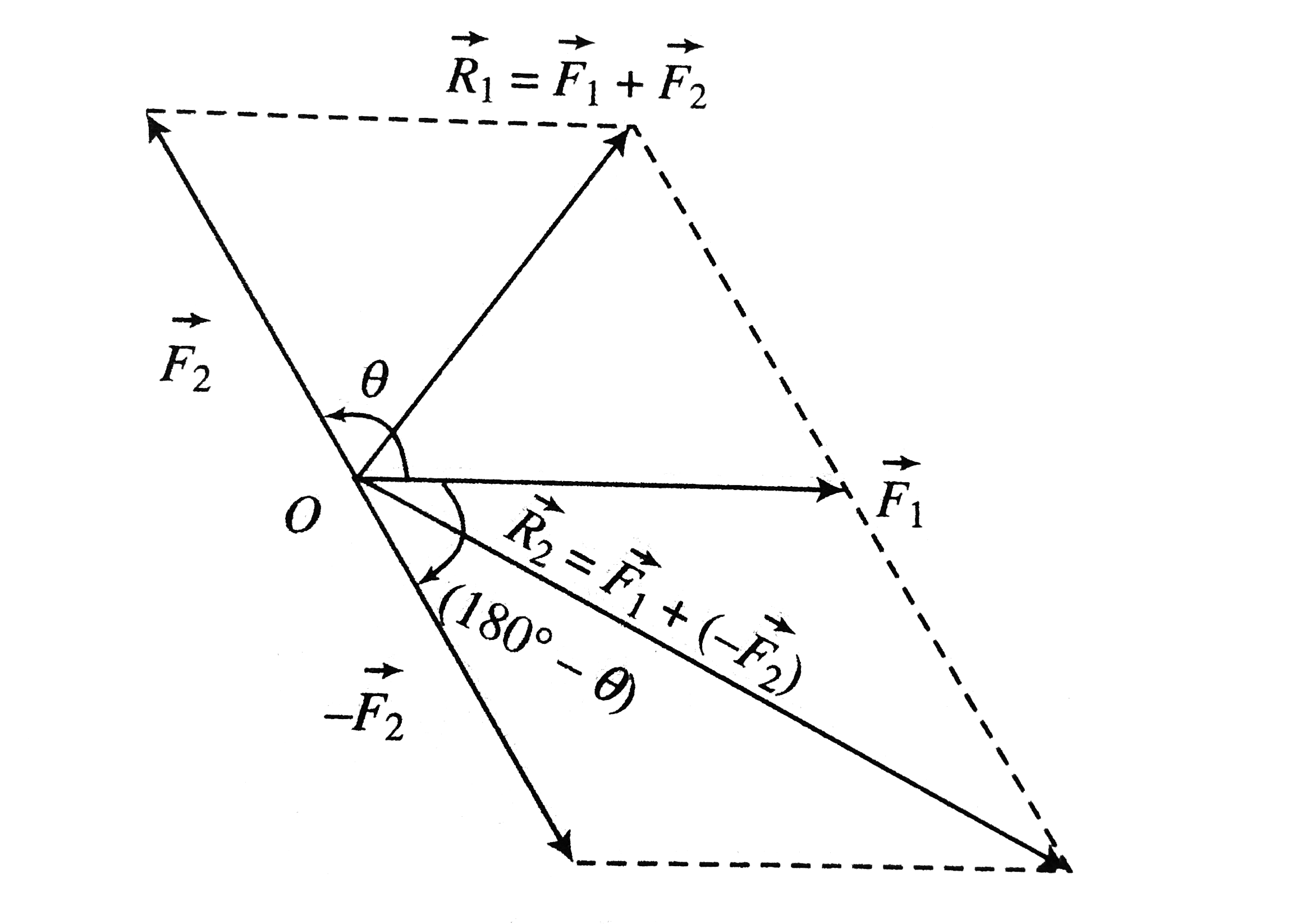
If the direction of ${\to F}_{2}$ is reversed,new
resultant force ${\to R}_{2} = {\to F}_{1} + (- {\to F}_{2})$ .
Using parallelogram law of vectors, the magnitude of new resultant is $∣ ∣ {\to R}_{2} ∣ ∣ = \sqrt{F_{1}^{2} + F_{2}^{2} + 2 F_{1} F_{2} cos θ}$ ..(ii)

since force is directly propotional to acceleration $\to F \propto \to a$ .
Hence, $\frac{∣ ∣ {\to R}_{2} ∣ ∣}{∣ ∣ {\to R}_{1} ∣ ∣} = \frac{a_{2}}{a_{1}} = \sqrt{\frac{3}{1}}$
From Eqs.(i) (ii) ,
$\frac{\sqrt{F_{1}^{2} + F_{2}^{2} - 2 F_{1} F_{2} cos θ}}{\sqrt{F_{1}^{2} + F_{2}^{2} + 2 F_{1} F_{2} cos θ}} = \sqrt{3}$
$\Rightarrow F_{1}^{2} + F_{2}^{2} + 4 F_{1} F_{2} cos θ = 0$ ..(iii)
Here $θ = 120^{\circ}$ and dividing Eq.(iii) by $F_{2}^{2}$ ,
${(\frac{F_{1}}{F_{2}})}^{2} + 1 - 2 (\frac{F_{2}}{F_{1}}) = 0$ ..(iv)
Let $\frac{F_{1}}{F_{2}} = x$ .Equation (iv)becomes ${(x)}^{2} + 1 - 2 (x) = 0$
after solving , $x = 1 or \frac{F_{1}}{F_{2}} = 1$ .

Updated on:21/07/2023

Two forces of equal magnitude act at a point making an angle $θ$ with each other. If the direction of one of the forces is reversed, the direction of the resultant will turn through
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
Eleven forces each equal to $5 N$ act on a particle simultaneously.If each force makes an angle $30^{\circ}$ with the next one, the resultant of all forces is
A $15 N$
B $55 N$
C $5 N$
Dzero
Two forces of magentude 7 newton and 5 newton act on a particle at an angle $θ$ can have any value . The minimum magnitude of the resultant forces is :
A5 newton
B8 newton
C12 newton
D2 newton