Calculate the area enclosed under the curve f(x)=x2 between the limits x=2 and x=3 (figure)
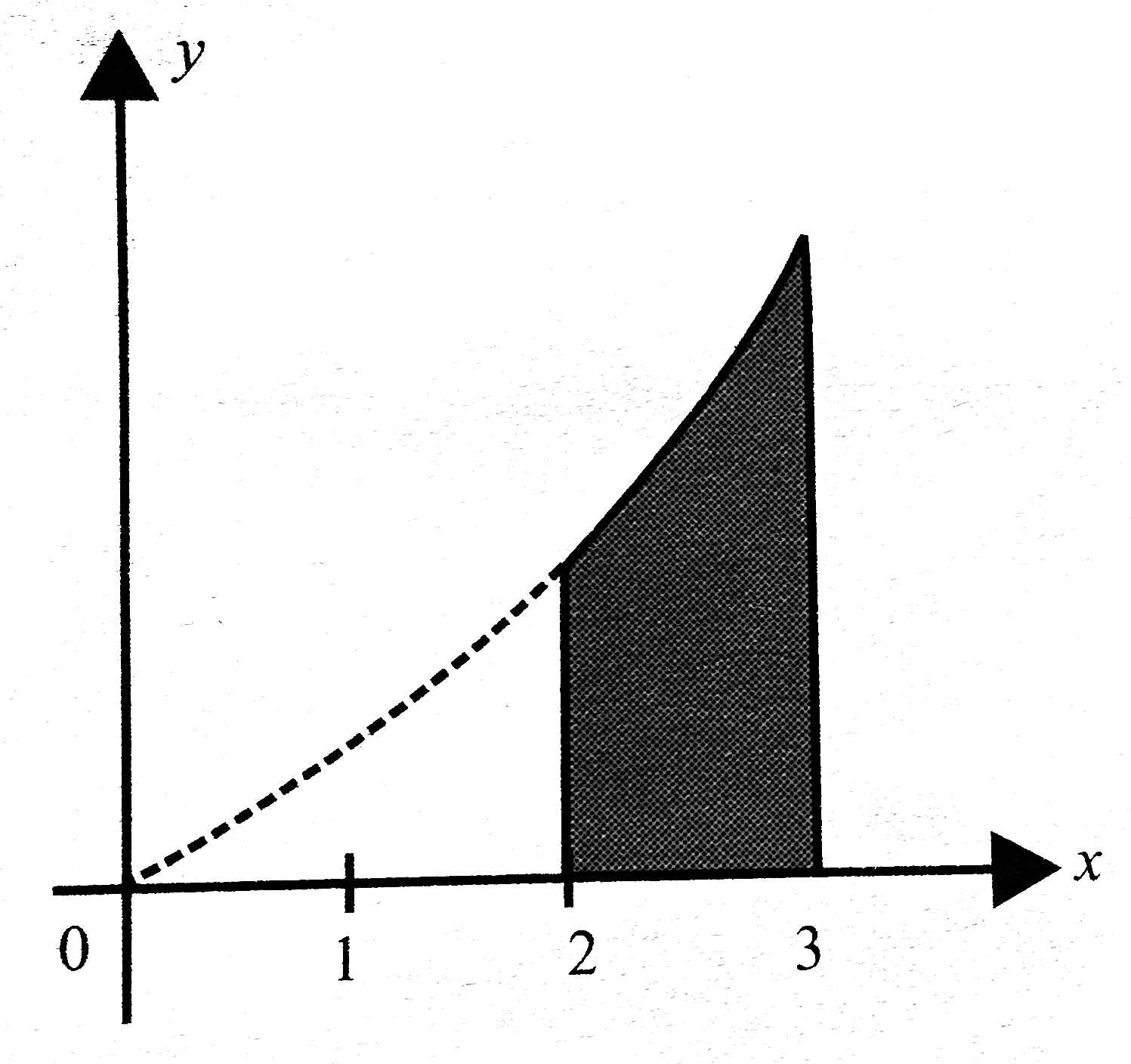
A
6.333
B
9.233
C
18.55
D
0
Video Solution
Text Solution
The correct Answer is:A
3∫2f(x)dx=3∫2x2dx
=x33∣∣∣32
=(3)33−(2)33=193=6.333
|
Topper's Solved these Questions
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Solved Examples
9 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.1
2 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer
4 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
Similar Questions
Knowledge Check
What is the area enclosed between the curve y2=12x and the lines x=0 and y=6?
A2 sq. unitsB4 sq. unitsC6 sq. unitsD8 sq. unitsWhat is the area enclosed by the curve 2x2+y2=1?
A2πBπCπ2Dπ√2
The area enclosed by the curve y2+x4=x2 is
View SolutionFind the area under the curve y=(x2+2)2+2x between the ordinates x =0 and x=2
View SolutionDetermine the area enclosed by the curve y=x3 , and the lines y=0,x=2 and x = 4.
View SolutionFind the area under the curve f(x)=2x from[0,2].
View SolutionCompute the area enclosed by the curve y2=(1−x2)3
View SolutionFind the area under the curve f(x)=x32 from[0,2]
View Solution
