The acceleration of a motorcycle is given by ax(t)=At−Bt2, where A=1.50ms−3 and B=0.120ms−4. The motorcycle is at rest at the origin at time t=0.
a. Find its position and velocity as funcitons of time.
b. Calculate the maximum velocity it attains.
a. When v0=0 and x0=0,
vx=∫t0(At−Bt2)dt=A2t2−B3t2
=(0.75ms−3)t3−(0.04ms−4)t3
x=∫t0(A2t2−B3t3)dt=A6t3−B12t4
=(0.25ms−3)t3−(0.010ms−4)t4
b. For the velocity to be a maximum, the acceleration must be zero, this occurs at t=0 and t=AB=12.5s. At t=0 the velocity is a minimum, and t=12.5s the velocity is
vx=(0.75ms−3)(12.5s)2−(0.040ms−4)(12.5s)3
=39.1ms−1
Topper's Solved these Questions
Similar Questions
The acceleration of a bus is given by ax(t)=at, where a=1.2ms−2.
a. If the bus's velocity at time t=1.0s is 5.0ms−1, what is its velocity at time t=2.0s?
b. If the bus's position at time t=1.0s is 6.0m, what is its position at time t=2.0s?
c. Sketch ax−t, vx−t, and x−t graphs for the motion.
View SolutionThe acceleration a in ms−2 of a particle is given by a=3t2+2t+2, where t is the time. If the particle starts out with a velocity v=2ms−1 at t=0, then find the velocity at the end of 2s.
View Solution
Knowledge Check
Velocity is given by v=4t(1−2t), then find time at which velocity is maximum
A0.25 sB1 sC0.45 sD4sA body starts from rest at time t=0 , the acceleration time graph is shown in the figure . The maximum velocity attained by the body will be
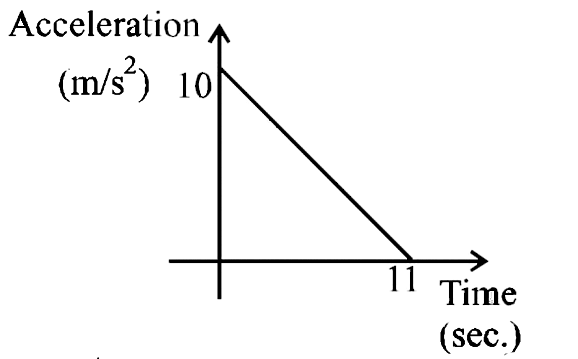 A110m/sB55m/sC650m/s(a)D550m/s
A110m/sB55m/sC650m/s(a)D550m/s
The acceleration a in ms−2 of a particle is given by a=3t2+2t+2, where t is the time. If the particle starts out with a velocity v=2ms−1 at t=0, then find the velocity at the end of 2s.
View SolutionThe displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
View SolutionThe acceleration of a particle is given by a=t3−3t2+5, where a is in ms−2 and t is in second. At t=1s, the displacement and velocity are 8.30m and 6.25ms−1, respectively. Calculate the displacement and velocity at t=2s.
View SolutionSita is driving along a staight highway in her car. At time t=0, when Sita is moving at 10ms−1 in the positive x-direction, she passes a signpost at x=50m. Here acceleration is a function of time:
a=2.0ms−2−(110ms−3)t
a. Derive expressions for her velocity and position as functions of time.
b. At what time is her velocity greatest?
c. What is the maximum velocity?
d. Where is the car when it reaches the maximum velocity?
View SolutionThe instantaneous position of a moving drone is given by y=m+nt2, where m=6m and n=3.2 ms−2 and t is time. Find the velocity, the average velocity of drone between t=0 sec and 4 sec. also calculate the velocity at t=3sec.
View SolutionThe displacement s of a particle at a time t is given bys=t3−4t2−5t. Find its velocity and acceleration at t = 2.
View Solution

