The energy E of an oscillating body in simple harmonic motion depends on its mass m, frequency n and amplitude a using the method of dimensional analysis find the relation between E ,m, n and a .
Mf/A2
MfA−2
Mf2A−2
MF2A2
The correct Answer is:D
E∝mafbAc
ML2T−2=maT−bLc
∴a=1,b=2,c=2
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Linked Comprehension
Explore 3 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Archives - Subjective
Explore 4 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Single Correct
Explore 93 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
The energy E of an oscillating body is simple harmonic motion depends on its mass m, frequency n and emplitude a using the method of dimensional analysis find the relation between E ,m, n and a .
View SolutionThe energy E of an oscillating body in simple harmonic motion depends on its mass m, frequency n and amplitude A as E= k(m)x(n)y(A)z.Find the value of (2x+y+z) [Amplitude is distance]
View Solution
Knowledge Check
Frequency of variation of kinetic energy of a simple harmonic motion of frequency n is
A2nBnCn2D3nA mass m oscillates with simple harmonic motion with frequency f=ω2πand amlitude A on a spring with constant K. therefore
Athe total energy of the system is 12KA2BThe frequency is 12π√KMCThe maximum velocity occurs, when x=0Dall the above are correctA : If displacement y of a particle executing simple harmonic motion depends upon amplitude a angular frequency ω and time t then the relation y=asinωt cannot be dimensionally achieved.
R : An equation cannot be achieved by dimensional analysis, if it contains dimensionless expressions.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion, then mark (1).BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark (2).CIf Assertion is true statement but Reason is false, then mark (3).DIf both Assertion and Reason are false statements, then mark (4).
A body is executing simple harmonic motion with frequency 'n' the frequency of its potential energy is
View SolutionIf the frequency of oscillation of a pendulum in simple harmonic motion is n, then frequency of pendulum whose length becomes four times is
View SolutionIf the period of oscillation of particle performing simple harmonic motion is 8 s, than the frequency of its kinetic energy will be
View SolutionA mass m oscillates with simple harmonic motion with frequency f=ω2π and amplitude A on a spring of stiffness constant K. Which of the following is not correct ?
View SolutionThe mass M shown in the figure oscillates in simple harmnonic motion and amplitude A. The amplitude of the point P is
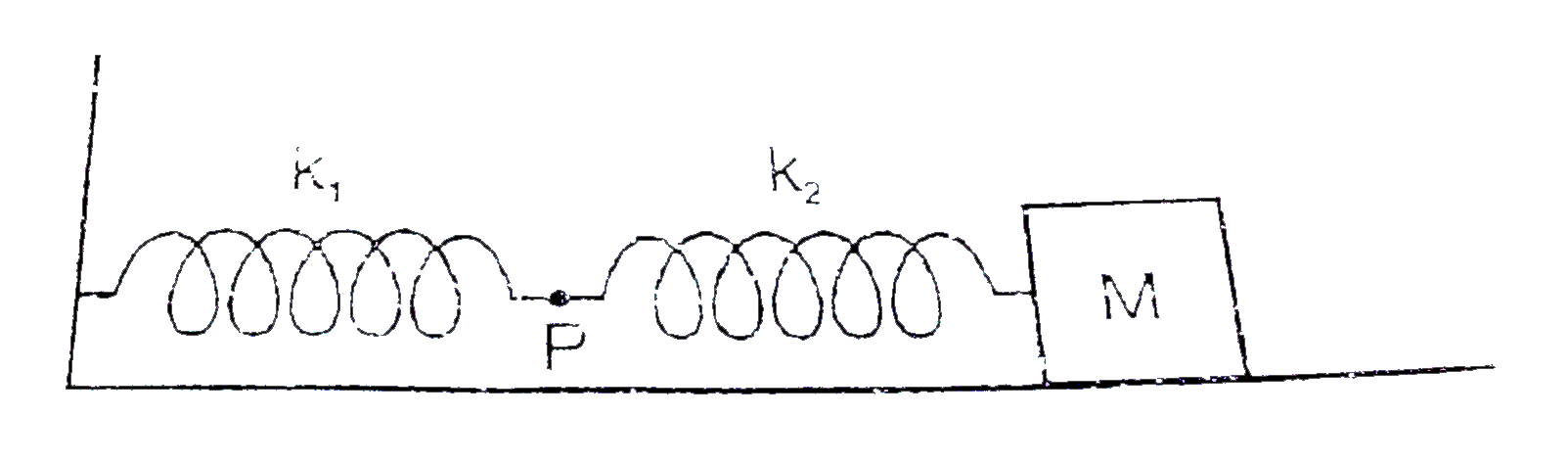
View Solution

