The mass of the liquid flowing per second per unit area of cross section of the tube is proportional to Pxandvy , where P is the pressure difference and v is the velocity , then the relation between x and Y is
x=y
x=−y
y2=x
y=−x2
The correct Answer is:B
MAt∝Pxvy
rArr ML−2T−1=[ML−1T−2]x[L1T−1]y=MxL−x+yT−2x−y
x=1,−x+y=−2,and−2x−y=−1
From here, we get y=−1 . Thus , x=−y.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Multiple Correct
Explore 2 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Linked Comprehension
Explore 3 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Subjective
Explore 31 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
The mass of the liquid flowing per second per unit area of cross-section of the tube is proportional to (pressure difference across the ends)^(n) and (average velocity of the liquid)^(m). Which of the following relations between m and n is correct?
View SolutionA conical section of a pipe is shown in figure through which water is flowing. Let A be the area of crosss-section, r be the radius of cross-section, P be the pressure at a point difference and v be the velocity of water.

Match the column-I with column-II containing values of ratio of quantities given in Column-I
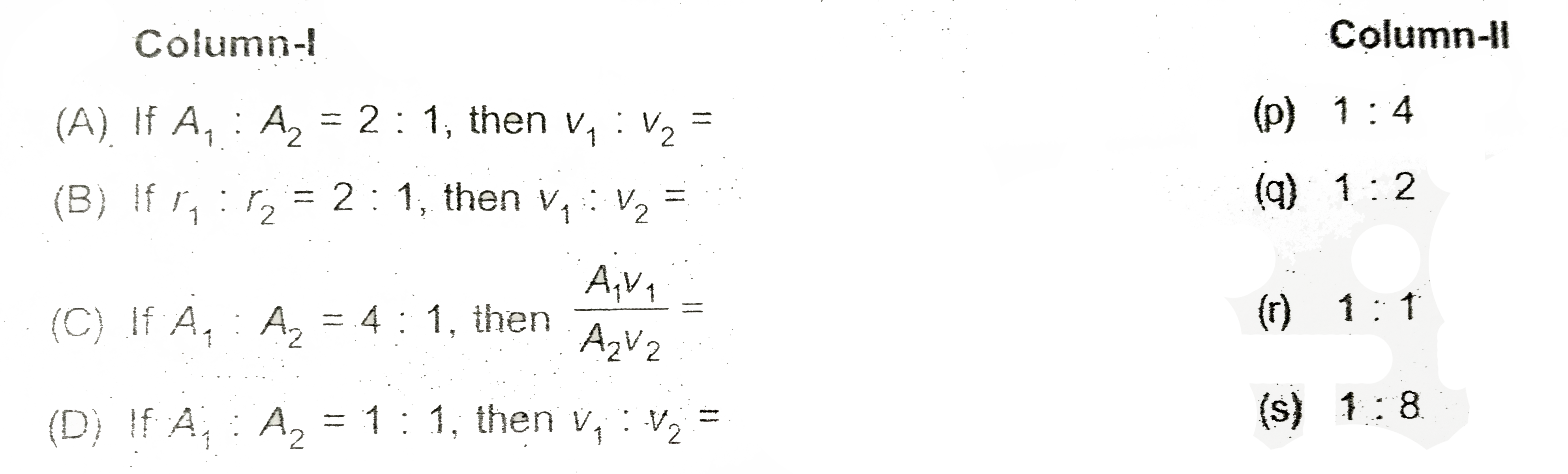
View Solution
Knowledge Check
If the wire has resistively per unit area of cross-section.the resistance between A and B is
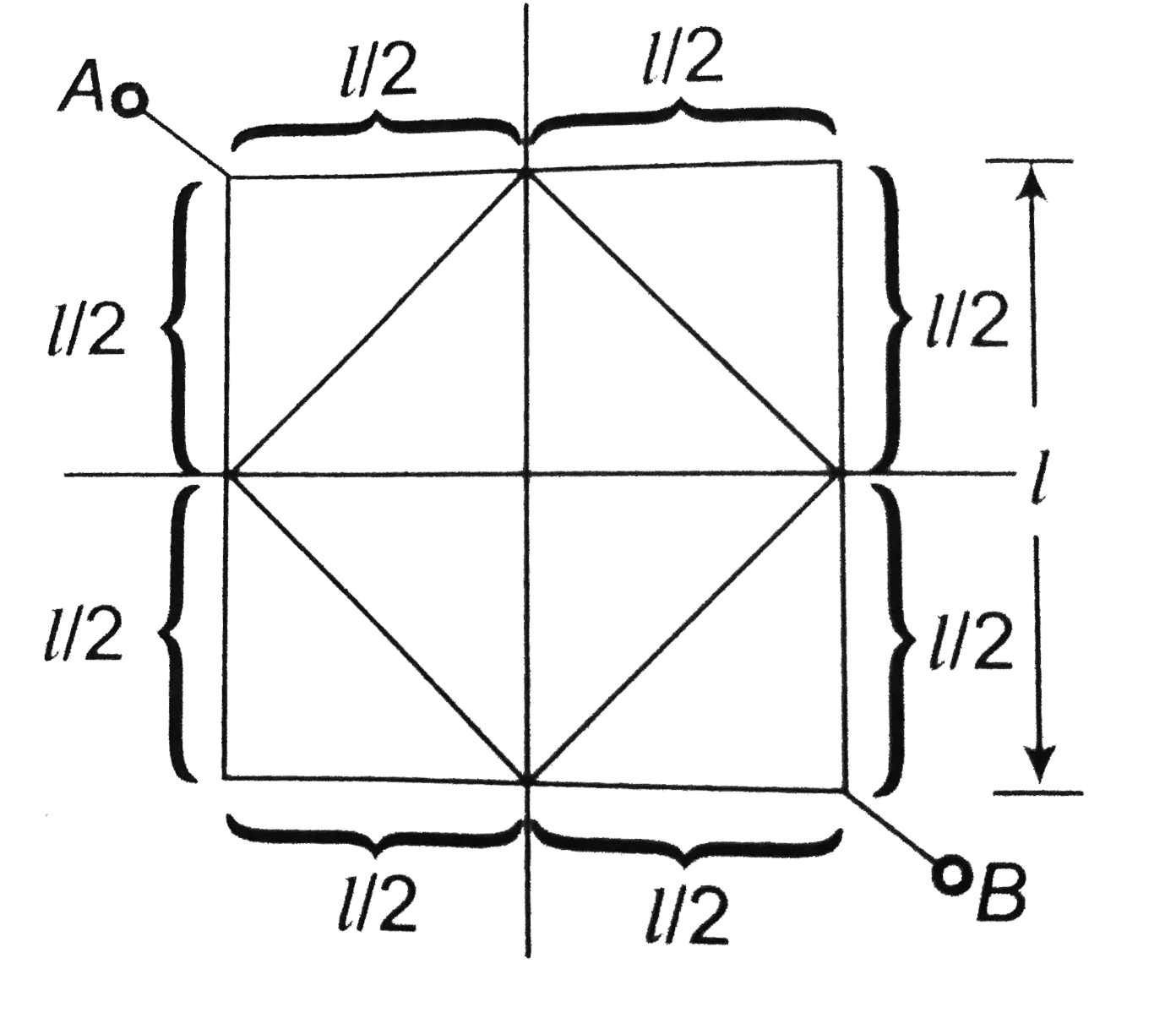 Aρl√2B√2ρlC2ρlDnone of these
Aρl√2B√2ρlC2ρlDnone of theseV is the volume of a liquid flowing per second through a capillary tube of length l and radius r, under a pressure difference (p). If the velocity (v), mass (M) and time (T) are taken as the fundamental quantities, then the dimensional formula for η in the relation V=πpr48ηl
A[MV−1]B[M1V−1T−2]C[M1V1T−2]D[M1V−1T−1]A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
 Athe volume of the liquid flowing through the tube in unit time is A1v1Bv2−v1=√2ghCv22−v21=2ghDthe energy per unit mass of the liquid is the same in both sections of the tube
Athe volume of the liquid flowing through the tube in unit time is A1v1Bv2−v1=√2ghCv22−v21=2ghDthe energy per unit mass of the liquid is the same in both sections of the tube
A non-viscous liquid of constant density 1000kg/m3 flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively 4×10−3m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
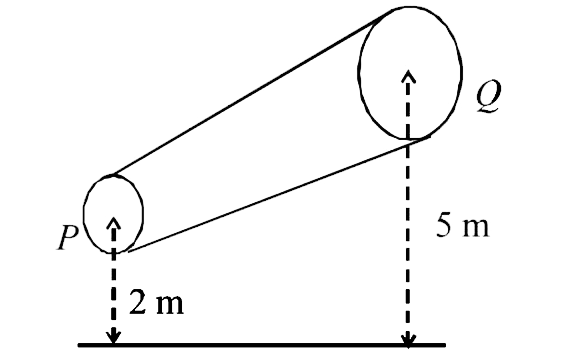
View SolutionThe volume of a liquid flowing per second through a capillary tube under a constant pressure difference is directly proportional to the_________power of radius.
View SolutionEqual volume of a liquid is poured into containers A and B where area of cross-section of container A is double the area of cross-section of container B. If PAandPB are pressures exerted at the bottom of the containers, then find PA:PB.
View SolutionA liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then

View Solution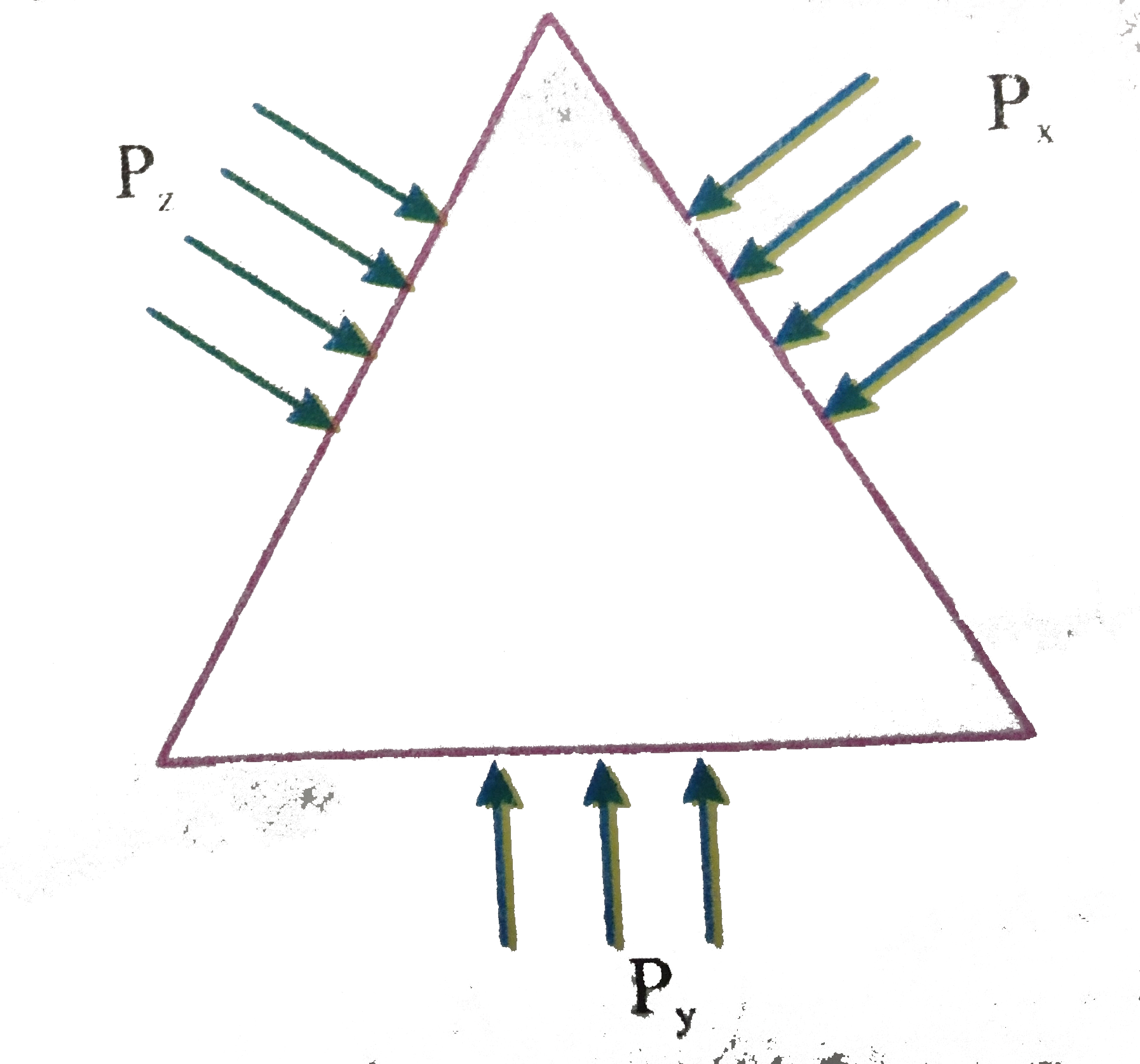
A triangular element of the liquid is shown in the fig. Px,Py and Pz represent the pressures on the element of the liquid then:
View Solution

