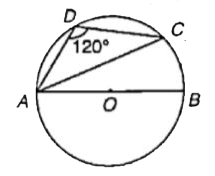
In the adjoining figure, O is the centre of the circle and AB is one of its diameter . If ∠ADC=120∘ , then the value of ∠BAC is Solution in Bengali
50∘
60∘
30∘
40∘
ABCD is a cyclic quadrilateral ∴∠ABC+∠ADC=180∘C (by theorem 38)
or , ∠ABC+120∘C=180∘or,∠ABC=180∘C−120∘C=60∘
Again , AOB is a diameter. ∴∠ACB is a semicircular angle,
∴∠ACB=90∘ [by theorem 35]
Then in ΔABC,∠BAC+∠ABC+∠ACB=180∘
or, ∠BAC+60∘+90∘=180∘[∵∠ABC=60∘and∠ACB=90∘]
or, ∠BAC=180∘−150∘=30∘
Hence (c) is correct.

Topper's Solved these Questions
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Write true or false
4 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Fill in the blanks:
6 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - EXERCISE - 1 (Long - answer type question )
9 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
Similar Questions
In the adjoining figure AD and BE are the perpendiculars on side BC and CA respectively of the ΔABC , Then , A, B, D, E are concyclic.
View SolutionAll angles in the same segment are……….
View SolutionProve that diameter is the greatest chord of a circle.
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View Solution(i) In the adjoining figure, O is the centre of the circle. If ∠OBC=35∘, then find the value of ∠BAC.

(ii) In the adjoining figure, O is the centre of the circle. If ∠OBC=40∘, then find the value of ∠BAC.

View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
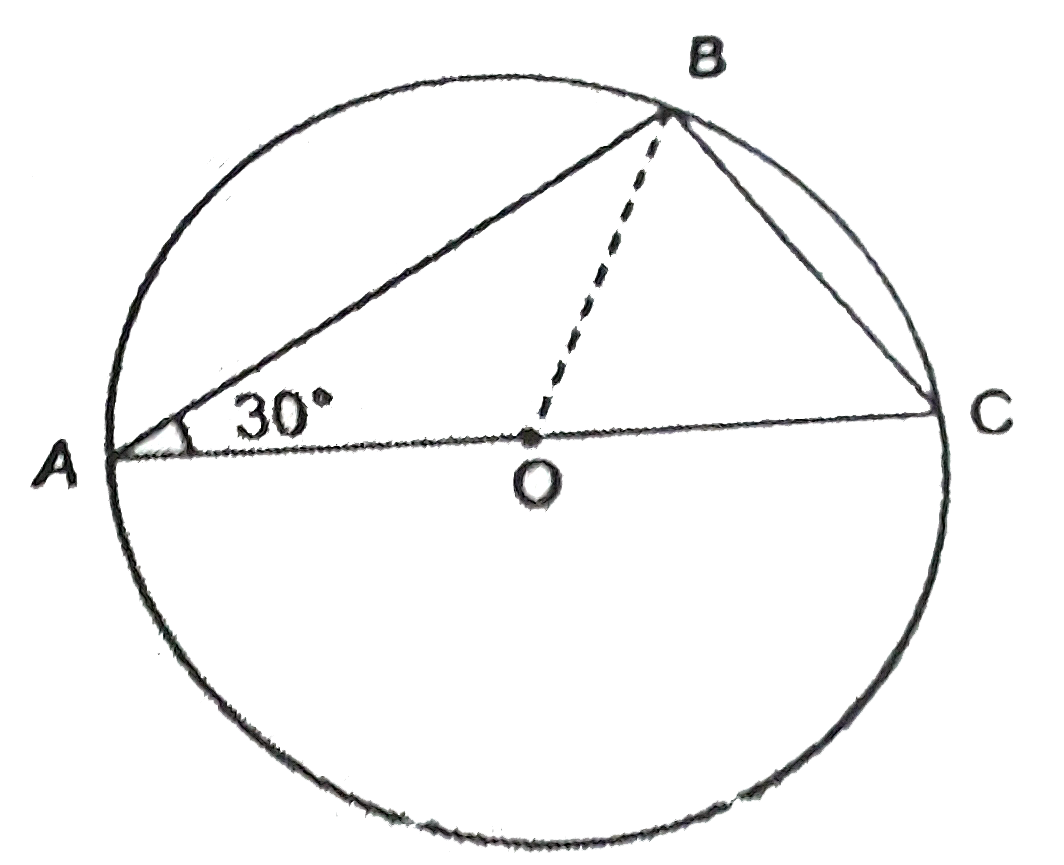
View SolutionIn the adjoining figure, O is the centre of the circle.If ∠BAC=40∘, then find the value of ∠ADC.

View Solutionसंलग्न चित्र में, ABCD एक चक्रीय चतुर्भुज है जिसकी भुजा AB वृत्त का एक व्यास है | यदि ∠ADC=140∘, तो ∠BAC का मान ज्ञात कीजिए |
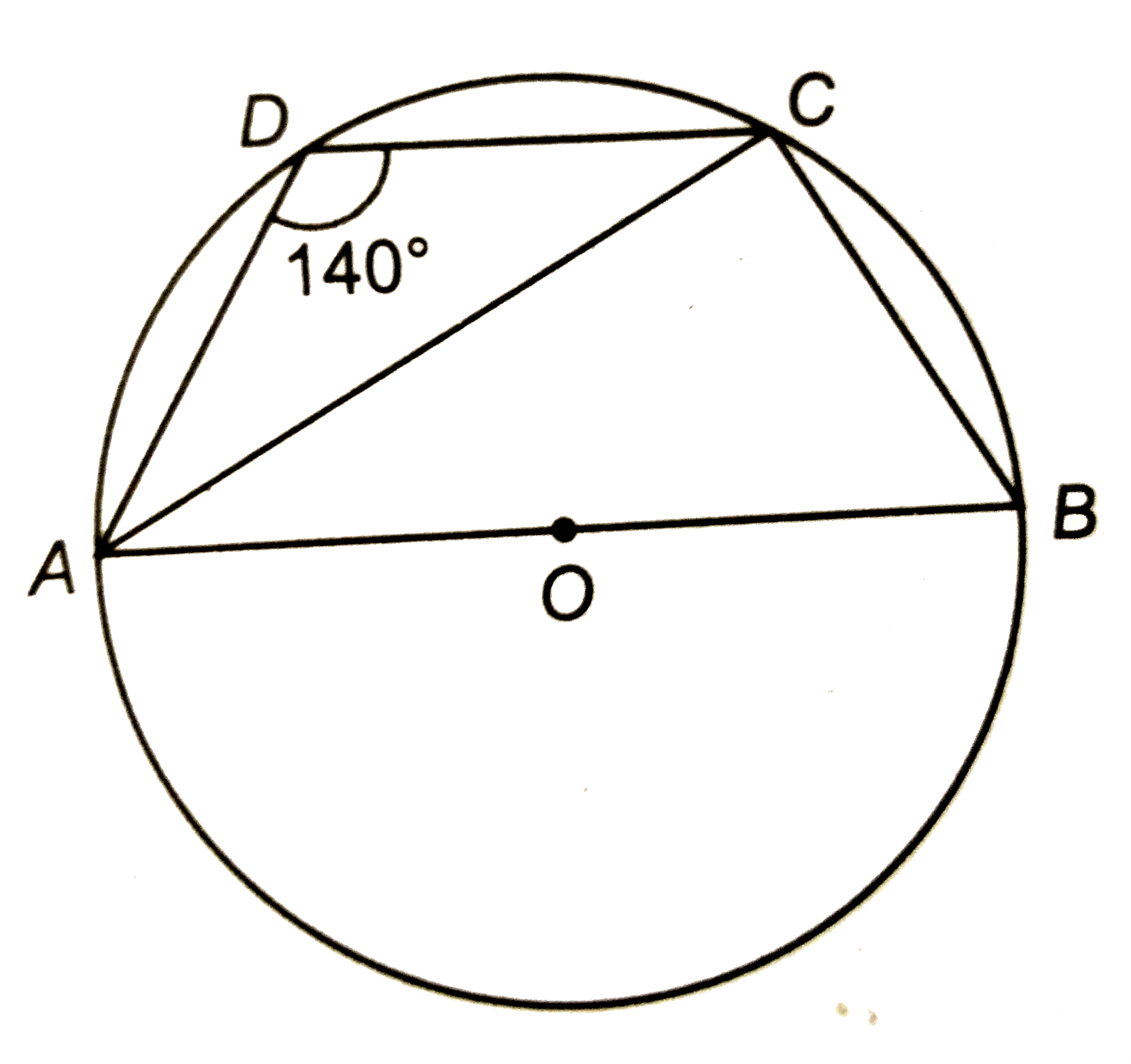
View SolutionIn the adjoining figur , O is the center of the circle and AB is one of its diameter. ABCD is a cyclic quadrilateral in wich AB||DC and if ∠BAC=25∘ , then the value of ∠DAC IS
View SolutionIn the figure □ ABCD is a cyclic quadrilateral.Seg AB is a diameter . If ∠ADC=120∘ , complete the following activity to find the measure of ∠BAC.
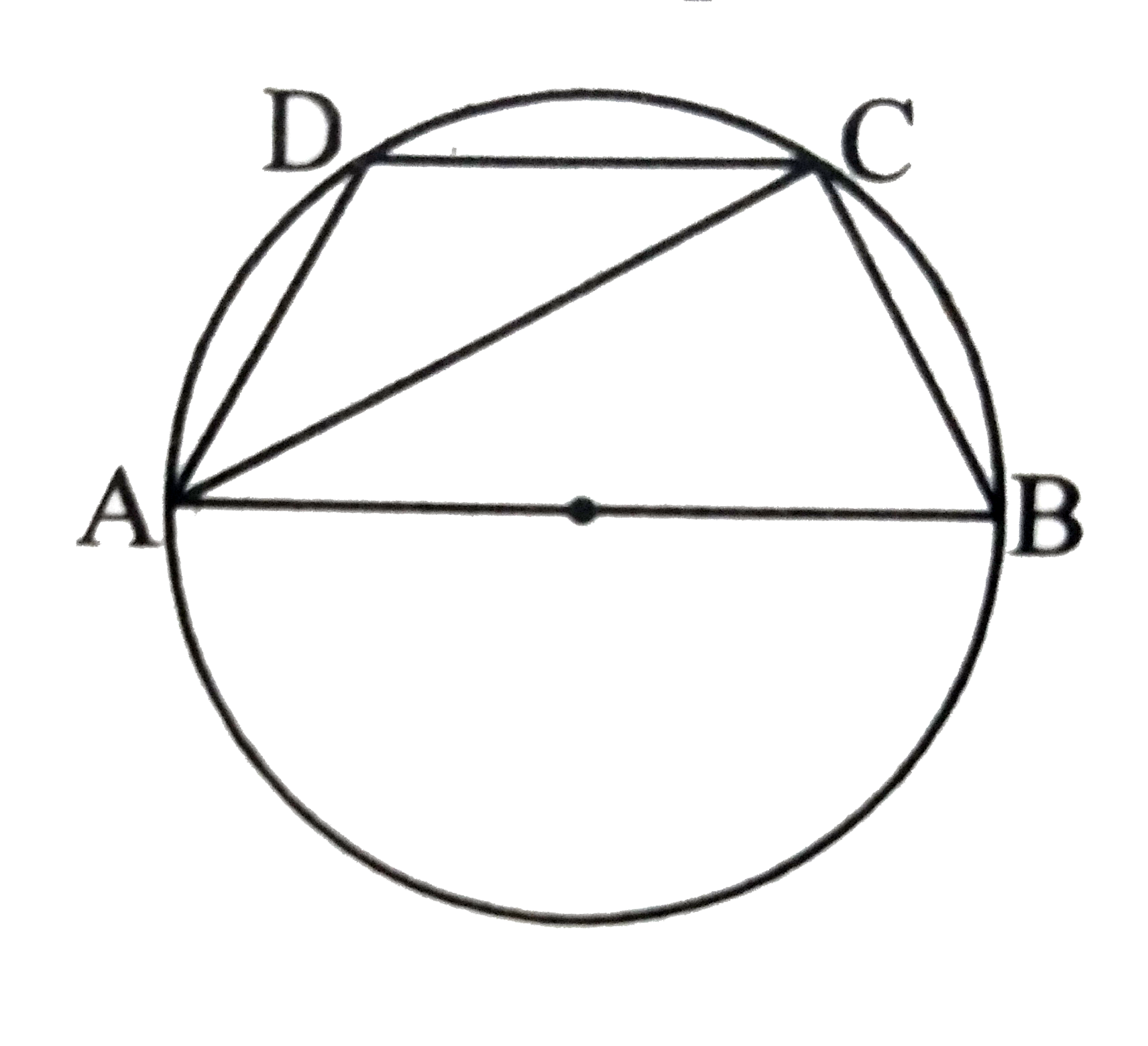
View SolutionIn the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
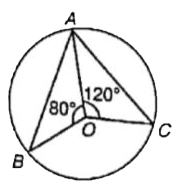
View SolutionIn the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
View Solutionदी गई आकृति में, O वृत्त का केन्द्र तथा AB उसका व्यास है। यदि ∠ADC=140∘ हो तो ∠CAB का मान ज्ञात करे।
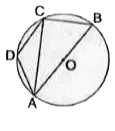
View Solutionबगल की आकृति में ABCD एक चक्रीय चतुर्भुज है जिसकी भुजा AB वृत्त का व्यास है। यदि ∠ADC=130∘ हो तो ∠BAC का मान ज्ञात करे।
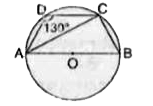
View Solution
