In □ABCD, seg AD∣∣ seg BC. Diagonal AC and digonal BD intersect each other in point P. Then show that APPD=PCBP.
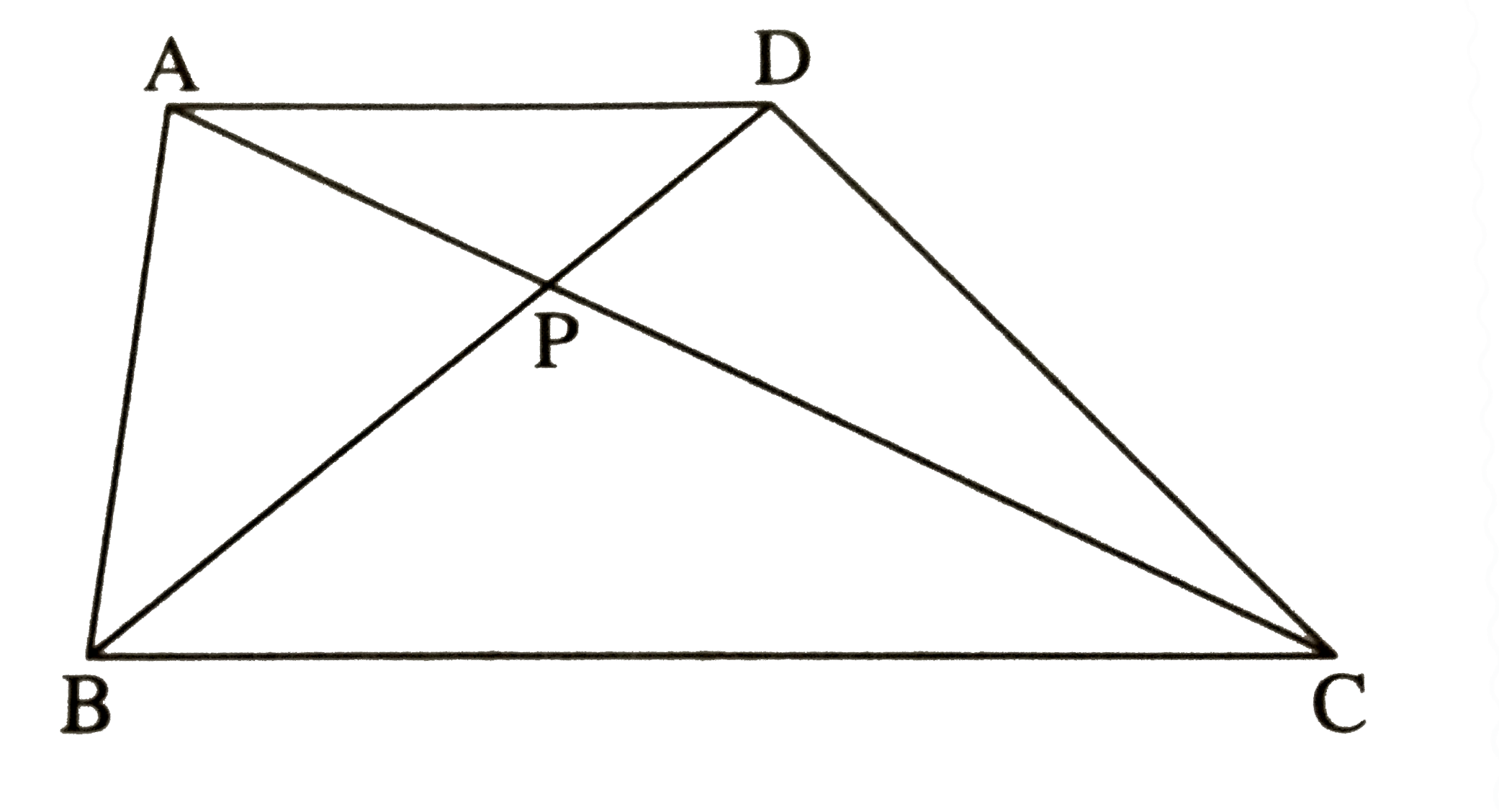
seg AD∣∣ seg BC and line DB is transversal,
∠ADP=∠CBP …….(Alternalte angles )…………1
In ΔADP and ΔCBP,
∠ADP≅∠CBP….[From 1]
∠APD≅∠CPB………..(Vertically opposite angles)
∴ΔADP~ΔCBP………..(AA test of similarity)
∴APCP=PDBP......(Corresponding sides of similar triangles are in proportion)
∴APPD=CPBP ...........(By alternendo)
i.e. APPD=PCBP
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - CHALLENGING QUESTIONS
8 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE
15 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)
3 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
Diagonals AC and BD of □ABCD intersect each other at point P. Show that ar(△APB)×ar(△CPD)=ar(△APD)×ar(△BPC)
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that AOBO=CODO.
View SolutionIn □ABCD , side BC∣∣ side AD. Digonals AC and BD intersect each other at P. If AP=13AC then prove DP=12BP.
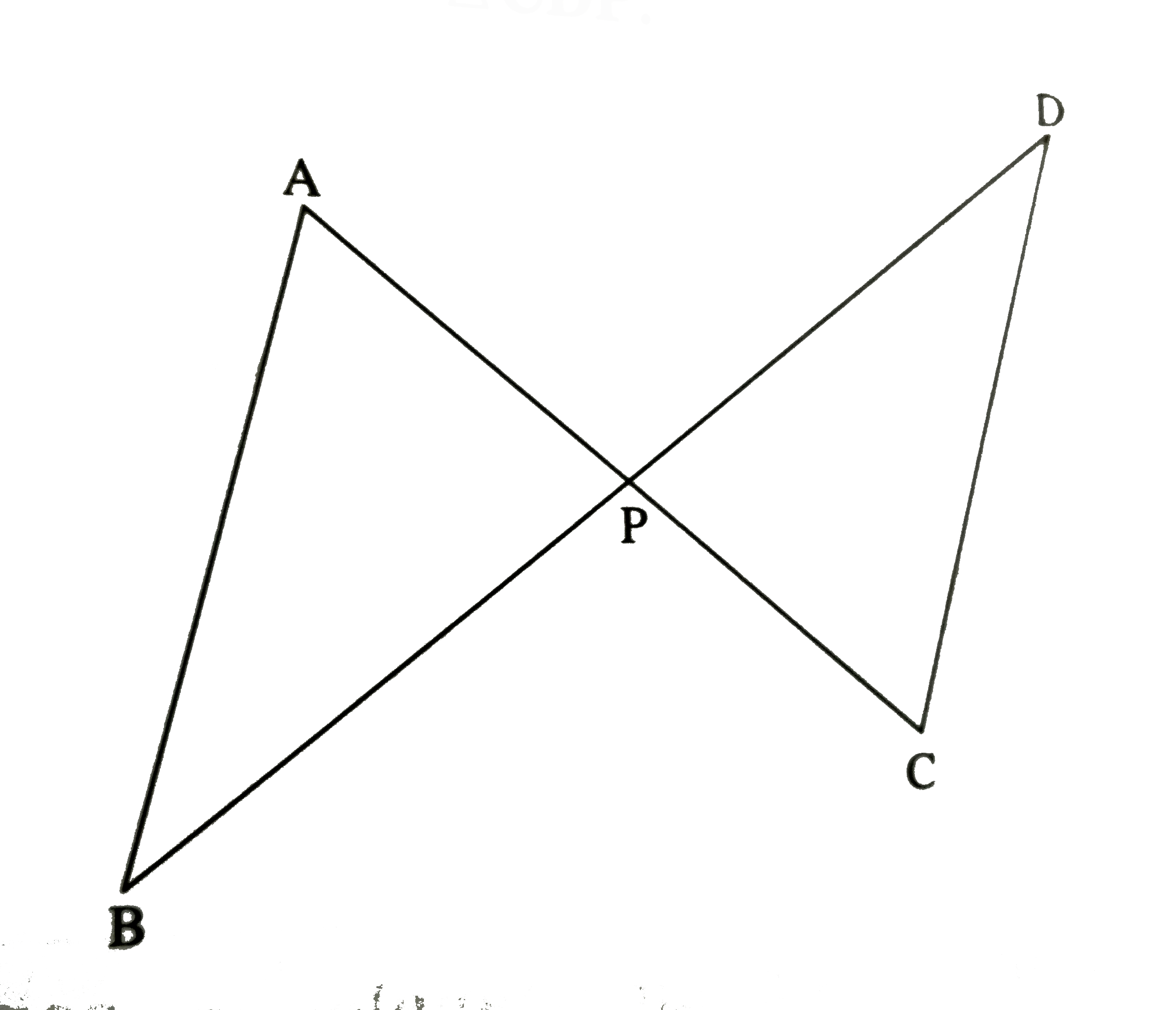
View SolutionIn the figure, seg AC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
View SolutionIn the figure, set aC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
View SolutionIn ABCD side BC || side AD. Seg AC and seg BD intersect in point Q. If AQ=1/3 AC then show that DQ=12BQ
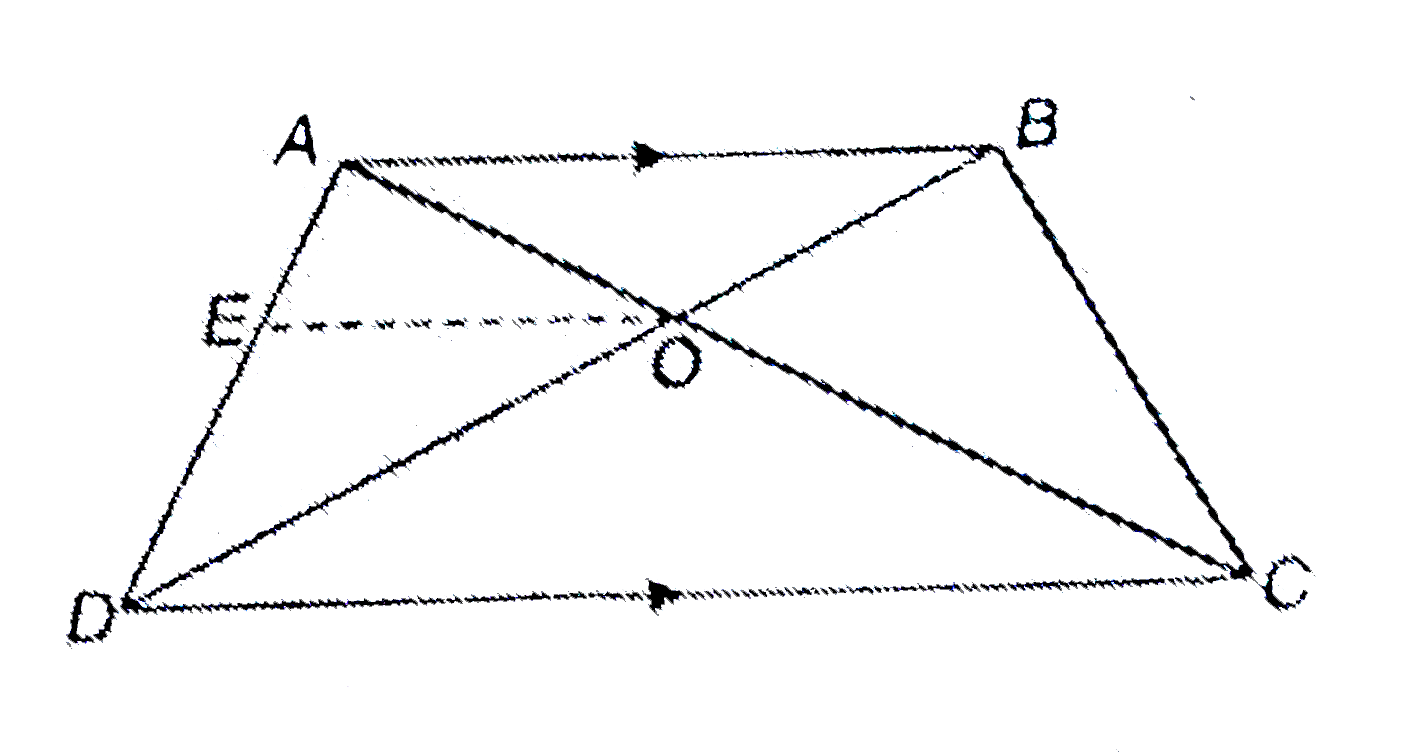
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View Solutionif ABCD is a trapezium, ACandBD are the diagonals intersecting each other at point Q. then AC:BD=
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View Solution
