ΔMNT~ΔQRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio A(ΔMNT)A(ΔQRS).

Let te altitude of ΔMNT drawn from vertex T be TX and the altitude of ΔQSR from vertex S be SY such that M−X−N and R−Y−Q.
TX=6 and SY=9
ΔMNT~ΔQRS ………..(Given)
∴M≅∠Q ......(Corresponding angles of similar triangles are congruent) .....1
In ΔMXT and ΔQYS
∠XMT≅∠YQS .......[From 1]
∠MXT≅∠QYS.(Each measures 90∘)
∴ΔMXT~ΔQYS...(AA test of similarity)
:TMSQ=TXSY...(Corresponding sides of similar triangles are in proportion)
∴TMSQ=59........2
ΔMNT~ΔQRS..........(Given)
A(ΔMNT)A(ΔQRS)=TM2SQ2
..............(Theorem of area of similar triangles)
∴A(ΔMNT)A(ΔQRS)=(TMSQ)2
∴A(ΔMNT)A(ΔQRS)=(59)2......[From 2]
∴A(ΔMNT)A(ΔQRS)=2581
∴A(ΔMNT)A(ΔQRS)=2581
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - CHALLENGING QUESTIONS
8 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE
15 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)
3 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
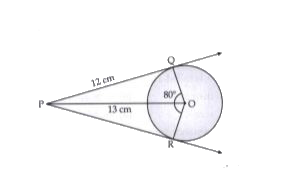
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the radius of the circle.
View SolutionThe length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is .
View Solution
Knowledge Check
In triangle ABC,BC=8 cm, AC=15 cm and AB=17 cm. The length of the altitude drawn from B on AC is :
A6 cmB7 cmC8 cmD10 cmThe length of a tangent drawn from a point 10 cm away from the centre of the circle of radius 5 cm is
A5 cmB5√3 cmC2√3 cmD√15 cmIn triangle ABC,BC=8 cm, AC=15 cm and AB=17 cm. The length of the altitude drawn from B on AC is :
A6 cmB7 cmC8 cmD10 cm
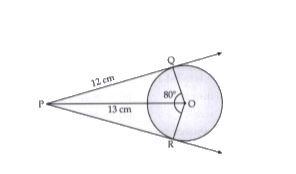
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the length of OR.
View Solution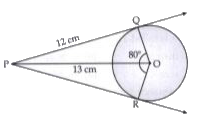
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the length of PR.
View SolutionFind the length of the perpendicular drawn from the point P (3, -4, 5) on the z-axis.
View Solution△ABC is an isoscles triangle with AB= AC= 13 cm and the length of altitude from A on BC is 5 cm, find BC.
View SolutionFind the length of the altitude of an equilateral triangle of side 9√3cm.
View Solution
