A large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

u2sin2αgcosθ
u2cos2αgcosθ
u2sin2α2gcosθ
u2sin2α2gsinθ
The correct Answer is:A
Take the x-axis along incline and y-axis perpendicular to the plane. ∴ Acceleration of particle =gsinθˆi+gcosθˆj and acceleration of block =gsinθˆi
∴ Acceleration of particle with respect to block
= acceleration of particle -acceleration of block
=(gsinθˆi+gcosθˆj)−(gsinθ)ˆi=gcosθˆj
Now motion of particle with respect to block will be a projectile as shown.
The only difference is, g will be replaced by g cos θ
∴PQ=Range(R)=u2sin2αgcosθ
PQ=u2sin2αgcosθ

Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - NCERT Exemplar
10 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Miscellaneous Questions
14 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A rectangular box is sliding on a smooth inclined plane of inclination θ. At t=0 the box starts to move on the inclined plane. A bolt starts to fall from point A. Find the time after which bolt strikes the bottom surface of the box.
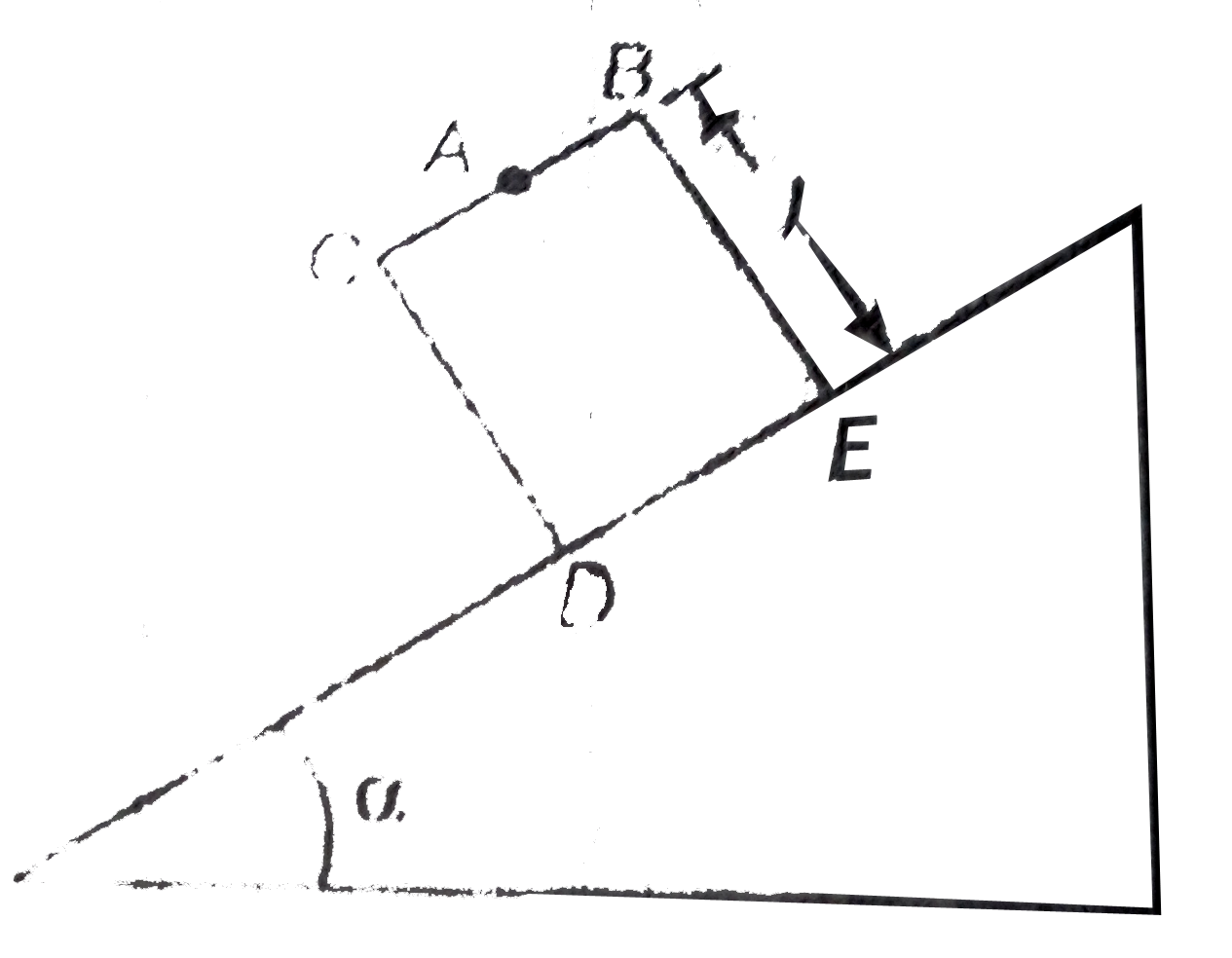
View SolutionA paricle is projected up from the bottom of an inlined plane of inclination α with velocity v0 If it returns to the points of projection after an elastic impact with the plane, find the total time of motion of the particle.
View Solution
Knowledge Check
in the question number 4, if the horizontal displacement of the particle as seen by an observer on the ground is zero, the speed of the box with respect to the ground at the instant when particle was projected is
AucosαBusinαcosθCucos(α+θ)cosθDusinθsinαcosθA particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
AucosθsecαBusecθcosαCucosθtanαDucosθcotαA box is failing freely. Inside the box, a particle is projected with some velocity v with respect to the box at an angle θ as shown in the figure.
 AThe path of the particle with respect to an observer sitting in the box will be a straight line.BThe acceleration of particle with respect to the box is zero.CThe path of the particle with respect to an observer sitting in the box will be a parabolaDThe acceleration of particle with respect to ground is g downward
AThe path of the particle with respect to an observer sitting in the box will be a straight line.BThe acceleration of particle with respect to the box is zero.CThe path of the particle with respect to an observer sitting in the box will be a parabolaDThe acceleration of particle with respect to ground is g downward
A particle is projected from the top of a tower of height H. Initial velocity of projection is u at an angle θ above the horizontal . Particle hits the ground at a distance R from the bottom of tower. What should be the angle of projection θ so that R is maximum ? What is the maximum value of R?
View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be

View Solution
