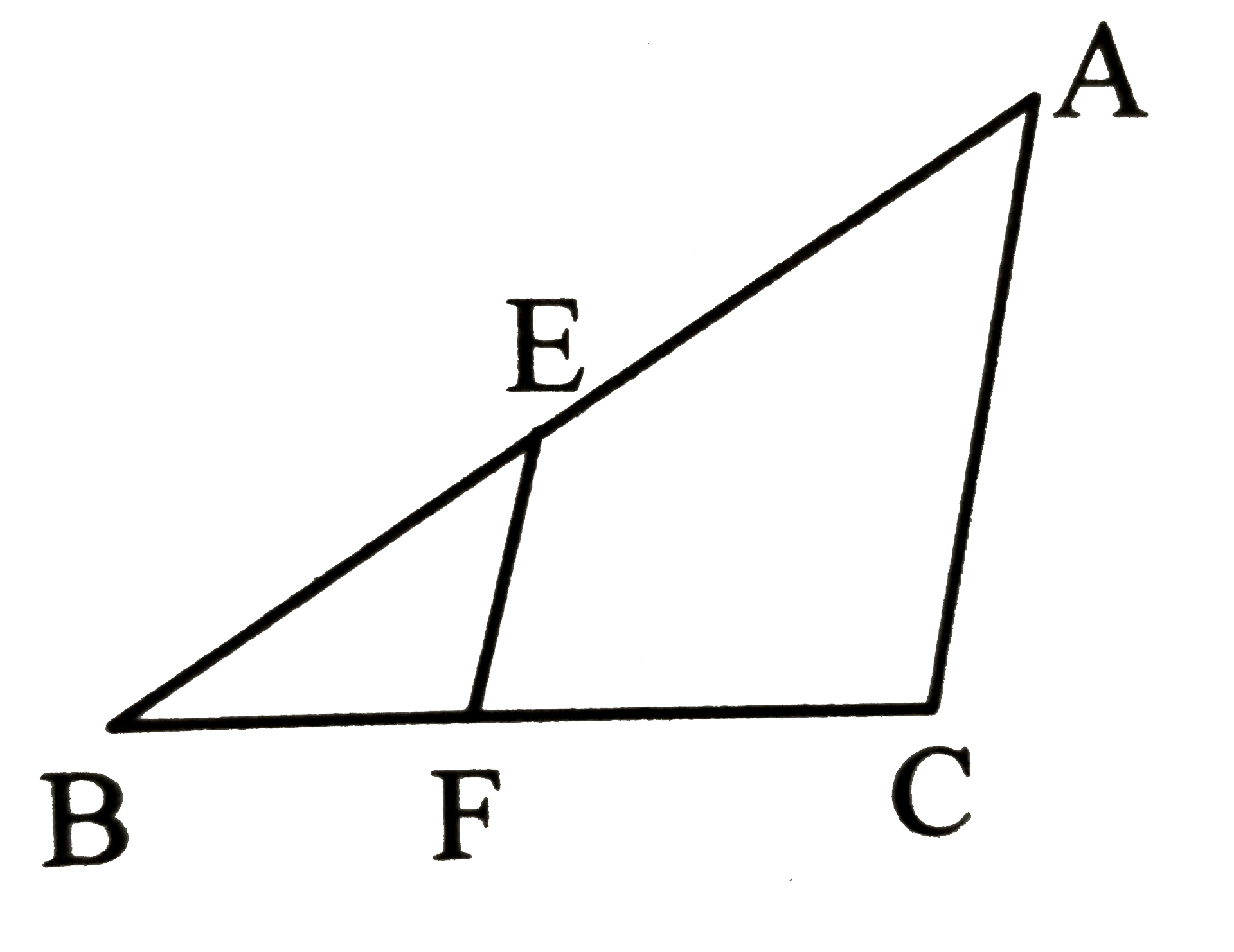
In the adjoining figure, seg XY∣∣ seg AC, IF 3AX=2BX and XY=9 then find the length of AC.
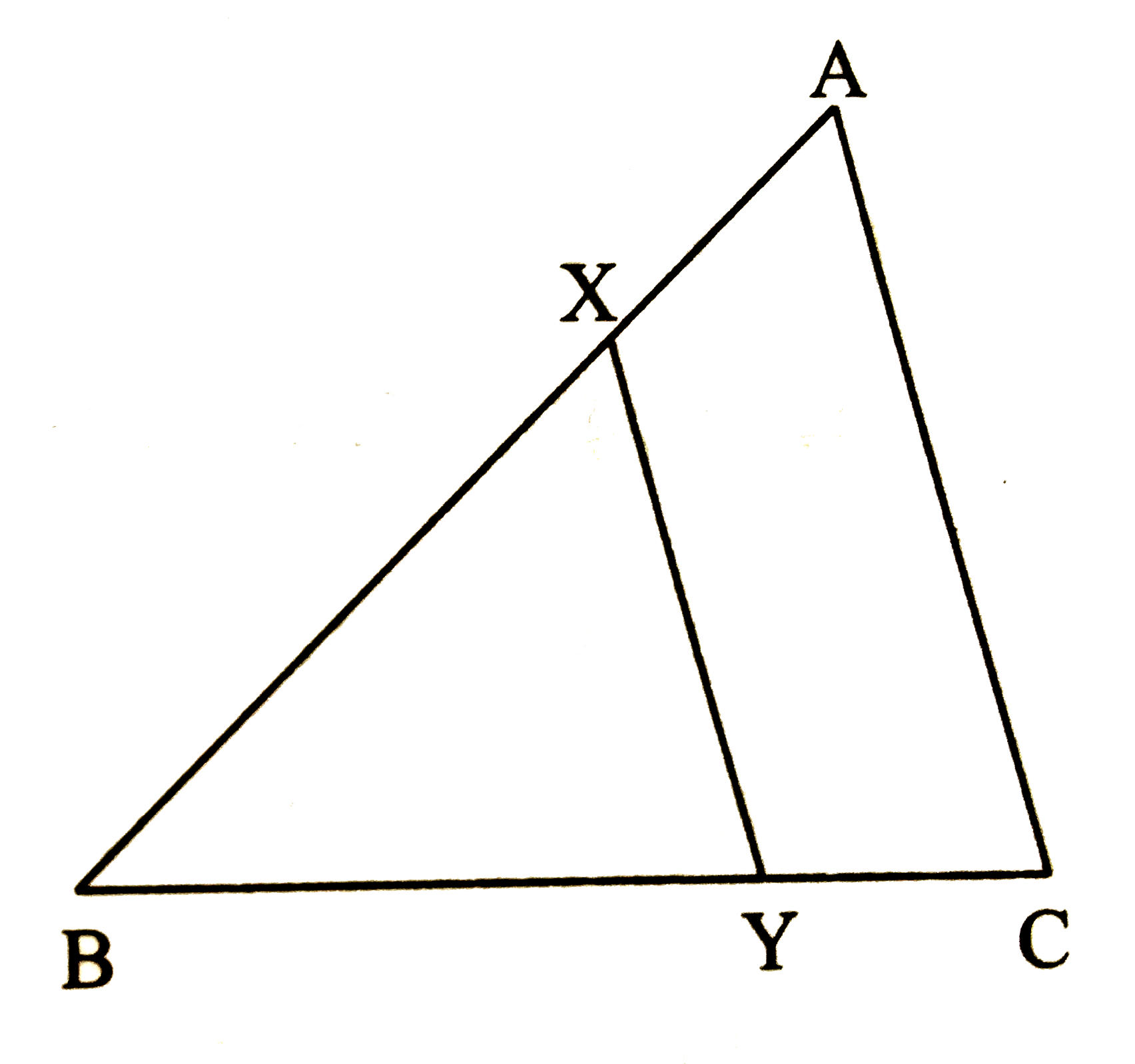
3AX=2BX
∴AXBX=23
By componendo, we get
AX+BXBX=2+33
ABBX=53
∴ by invertendo, we get
BXAB=35……(1)
In ΔBXY and ΔBAC ,
∠BXY≅∠BAC…….(Corresponding angles)
∠XBY≅∠ABC.......(Common angle)
∴ΔBXY~ΔBAC......("AA" test of similarity)
∴BXAB=XYAC......(Corresponding sides of similar triangle)
∴35=9AC........[From (1)]
∴3×AC=9×5
∴AC=9×53
AC=15
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)
3 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - EXAMPLE TYPE
50 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.3 (2 mark each)
10 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
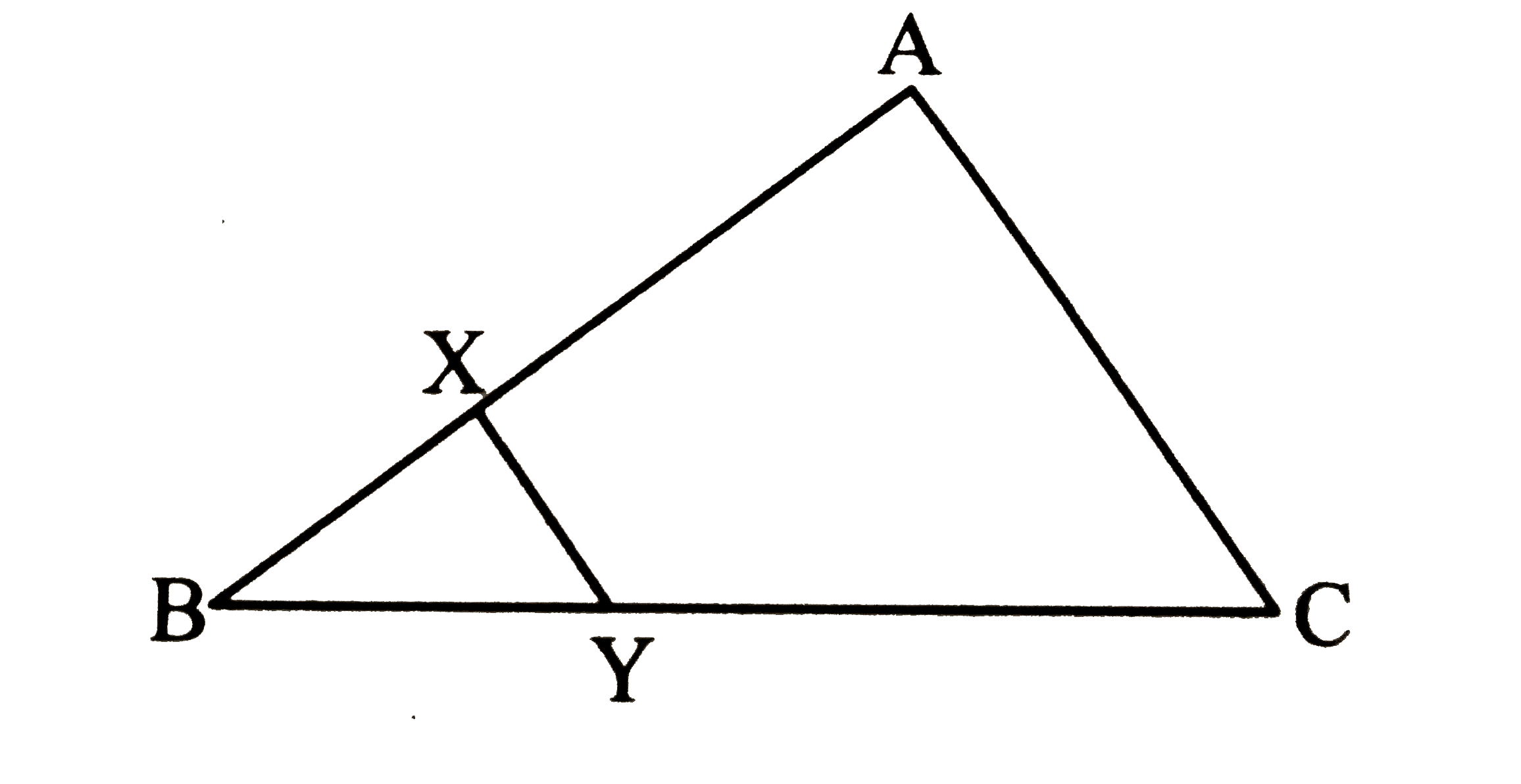
In the adoining figure, XY || seg AC. If 2 AX = 3 BX and XY = 9, find the value of AC.
View SolutionIn the adjoining figure, find AC . (FIGURE)
View SolutionIn figure XY∣∣ seg AC. If 2AX=3BX and XY=9, complete the activity to find the value of AC.
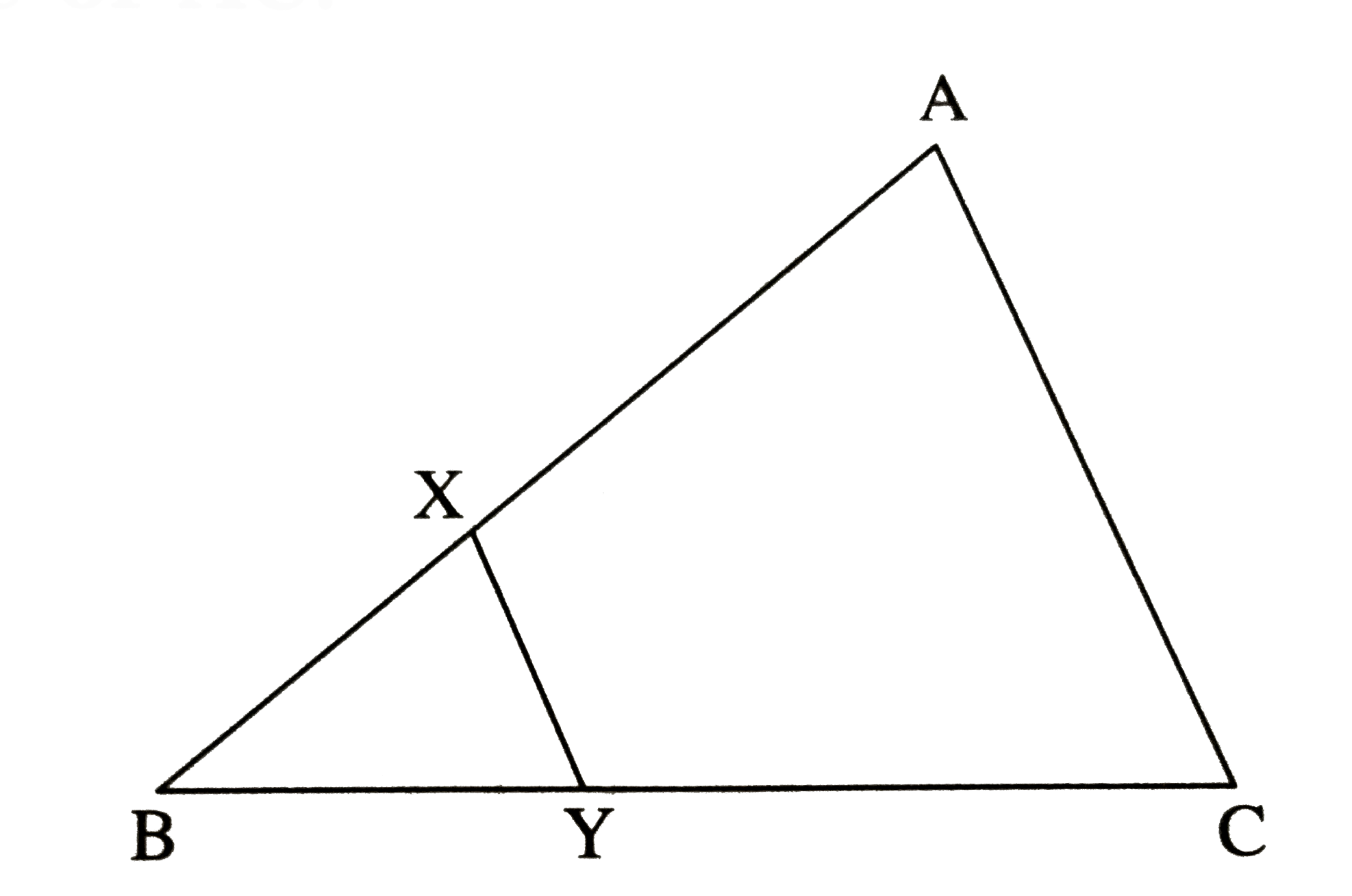
Activity: 2AX=3BX
∴AXBX=□□
∴AX+BXBX=□+□□.........(By componendo)
∴ABBX=□□.............1
ΔBCA~ΔBYX.......(□ test of similarity)
∴BABX=ACXY
..............(Corresponding sides of similar triangles)
∴□□=AC9
∴AC=□ ...........[From 1]
View SolutionIn the adjoining figure,AB=AC.Find the value of x
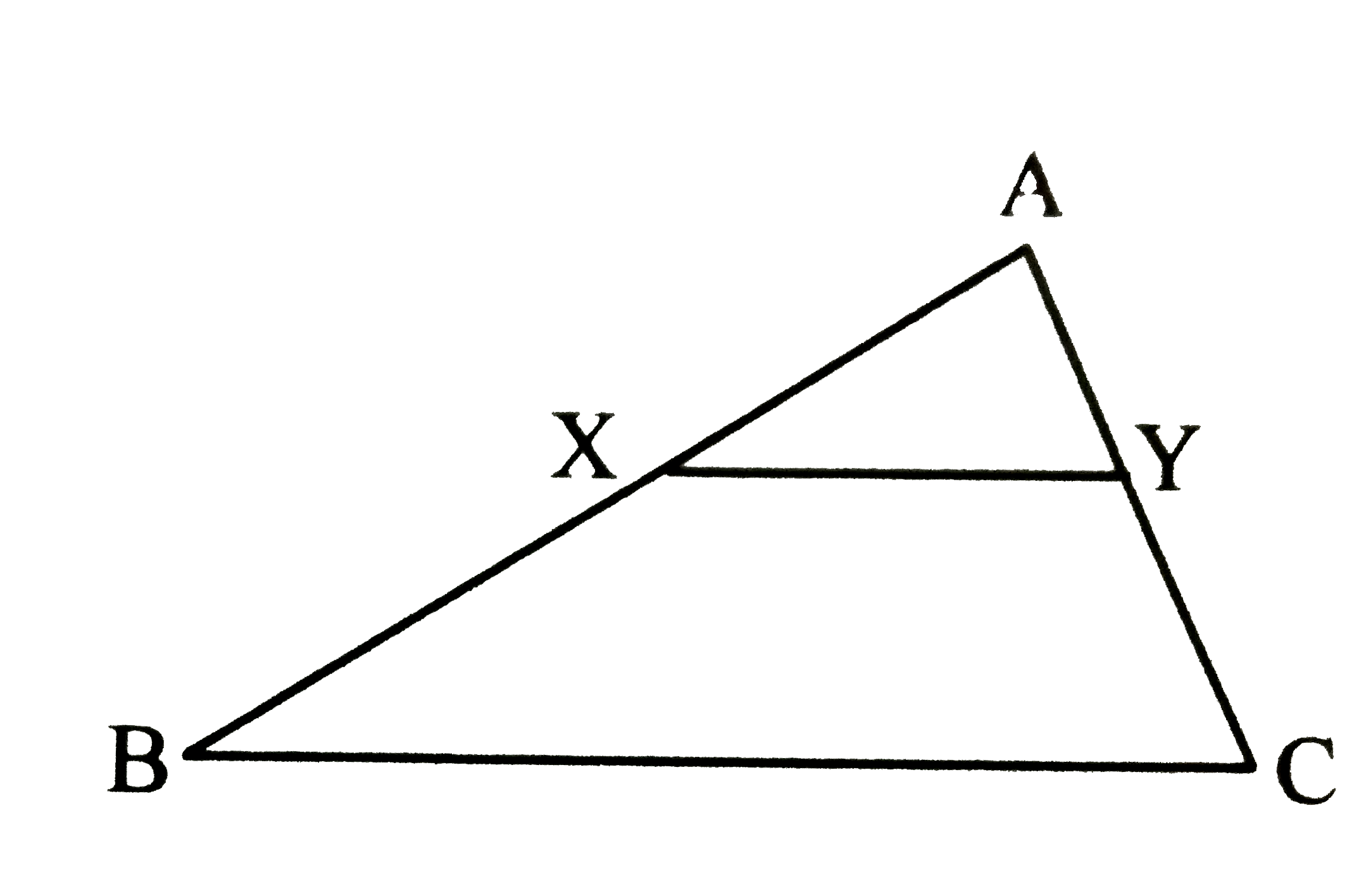
View SolutionIn the adjoining figure, seg XY ||seg BC, then which of the following statements is true?
View SolutionIn the adjoining figure, seg EF|| side AC, AB = 18, AE = 10, BF = 4. Find BC.
View SolutionPoint M is midpoint of seg AB. If AB =9 cm then find the length of AM.
View Solutionpoint C is the midpoint of seg AB. If AC = 5.5, then find the length of AB.
View SolutionIn the adjoining figure, seg PA , seg QB, seg RC and seg SD are perpendicular to line AD. AB = 60, BC = 70, CD = 80, PS = 280, then find PQ, QR and RS.

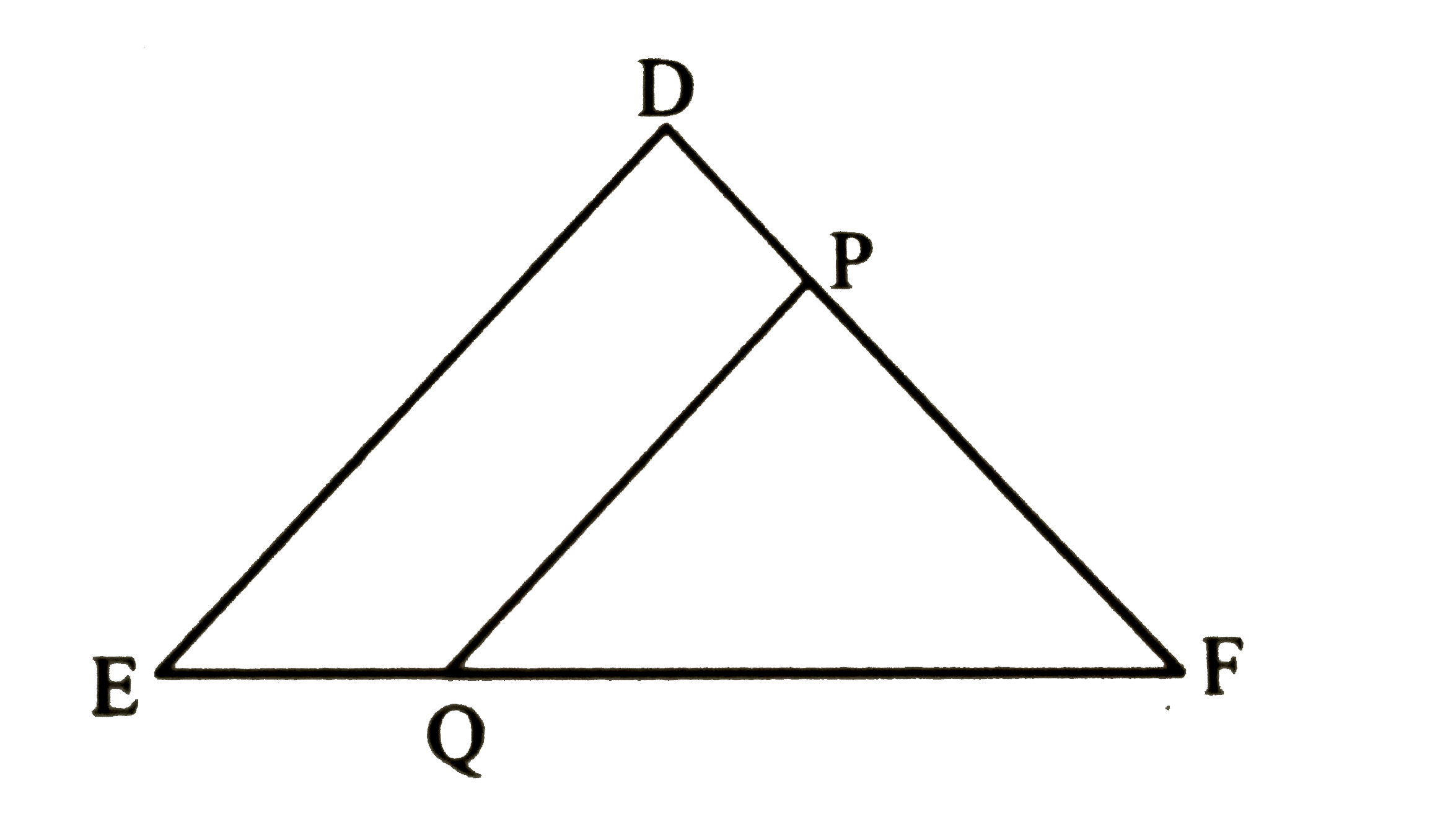
View SolutionIn the adjoining figure, seg PQ||seg DE, A(ΔPQF)=20 sq. uints, PF = 2 DP, then find A (□DPQE) by completing the following activity.
View Solution
