In the figure X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ∣∣ set DE, set QR∣∣ set EF. Fill in the blanks to prove that set PR∣∣ seg DF.
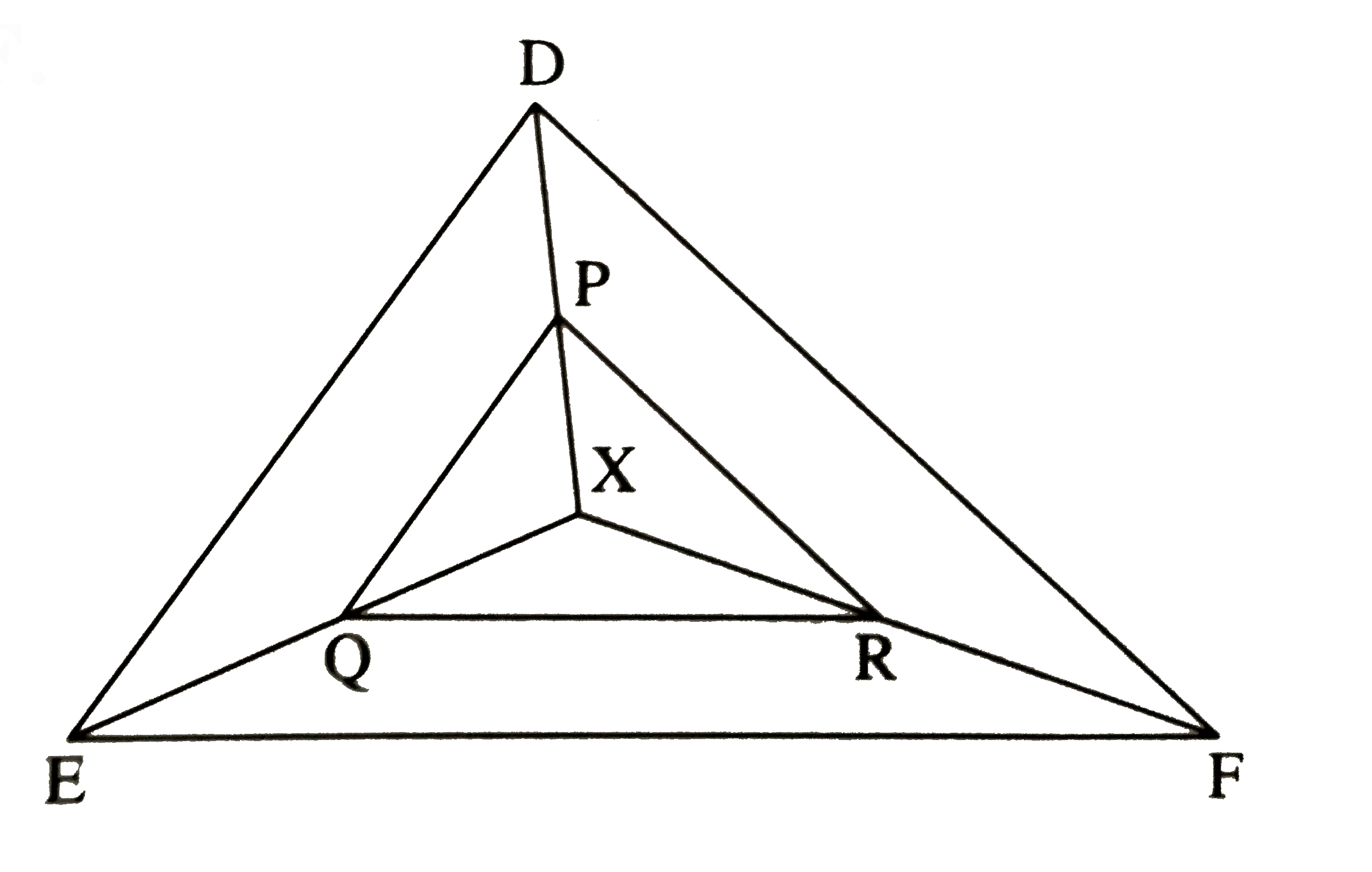
In ΔXDE, PQ∣∣DE .....(Given)
∴XPPD=XQQE..........(1)........(Basic proportionality theorem)
In ΔXEF, QR∣∣EF........(Given)
∴XQQE=XRRF..........(2)........(Basic proportionality theorem)
∴XPPD=XRRF.....[From (1) and (2)]
∴ seg PR∣∣ seg DF.......(Converse of basic proportionality theorem)
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)
3 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - EXAMPLE TYPE
50 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.3 (2 mark each)
10 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
S is any point in the interior of a △PQR . Prove that SQ+SR<PQ+PR
View SolutionIn a △PQR mark
the points X, Y, Z in the interior of △ PQR
View SolutionIf Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View SolutionTake any point O in the interior of a triangle PQR. Is (i) OP+OQ>PQ? (ii) OQ+OR>QR? (iii) OR+OP>RP?
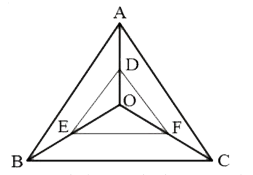
View SolutionIn the figure, a point O inside △ABC is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.
View SolutionIn the figure ΔPQR is an equilateral triangle. Point S is on seg QR such that
QS=13QR.
Prove that : 9PS2=7PQ2

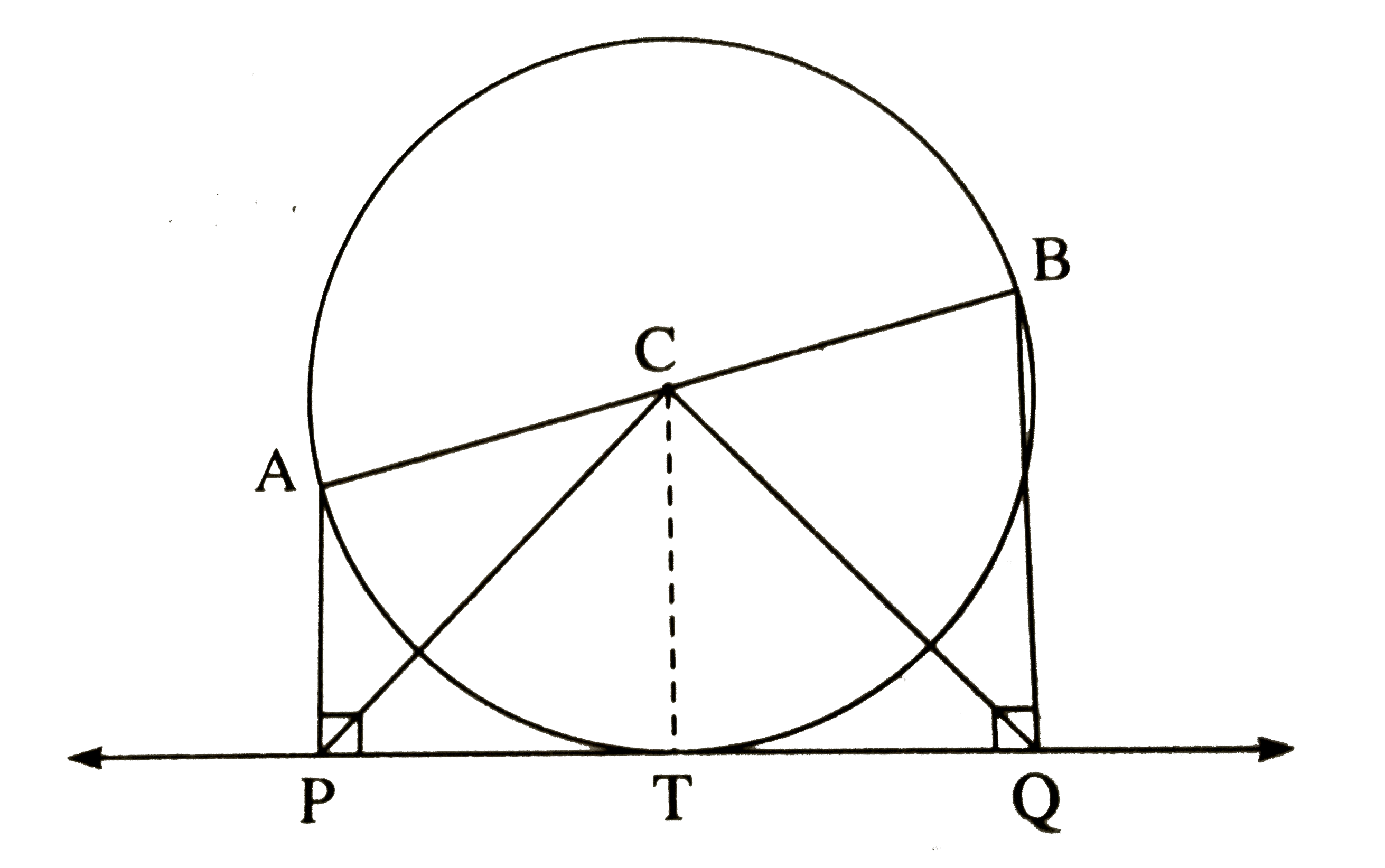
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

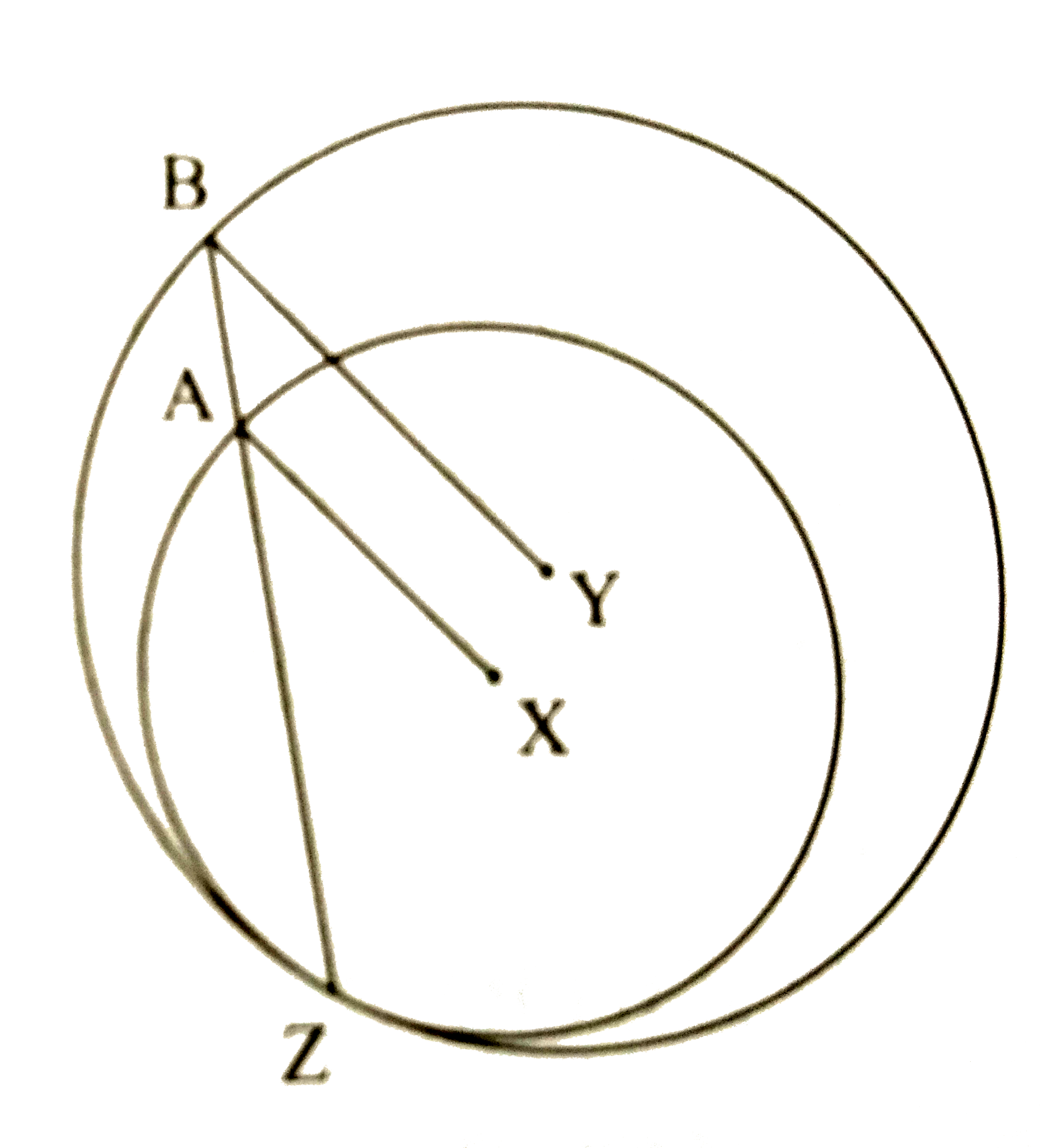
View SolutionIn the figure , circles with centres X and Y touch internally at point Z. Seg BZ is the chord of bigger circle and it intersects smaller k circle at point A.
Prove that seg AX∣∣ seg BY.
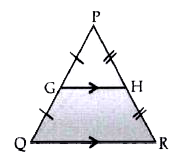
View SolutionIn the given figure G is the mid-point of the side PQ of ΔPQR and GH || QR .Prove that H is the mid -point of the side PR of the triangle PQR .
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
View Solution
