A perfectly straight portion of a uniform rope has mass M and length L. At end A of the segment, the tension in the rope is TA and at end B it is TB(TB>TA). Neglect effect of gravity and no contact force acts on the rope in between points A and B. The tension in the rope at a distance L/5 from end A is:-
TB−TA
(TA+TB)/5
(4TA+TB)/5
(T1−TB)/5
The correct Answer is:C
To find the tension in the rope at a distance L5 from end A, we can follow these steps:
Step 1: Understand the Problem
We have a uniform rope with mass M and length L. The tension at end A is TA and at end B is TB, where TB>TA. We need to find the tension TC at a point C which is located at a distance L5 from end A.
Step 2: Set Up the Force Equation
Since the tension increases from TA to TB, there must be a net force acting on the rope, which implies that the rope is accelerating. We can write the equation for the net force acting on the entire rope:
TB−TA=M⋅A
where A is the acceleration of the rope.
Step 3: Analyze the Segment of the Rope
Now, let's focus on the segment of the rope from point A to point C (length L5). The mass of this segment can be calculated as:
Mass of segment=ML⋅L5=M5
Step 4: Write the Force Equation for Segment AC
For the segment from A to C, we can write the force equation as follows:
TC−TA=(M5)⋅A
Step 5: Substitute for Acceleration
From Step 2, we have A=TB−TAM. Substitute this expression for A into the equation from Step 4:
TC−TA=(M5)⋅(TB−TAM)
Step 6: Simplify the Equation
This simplifies to:
TC−TA=15(TB−TA)
Step 7: Solve for TC
Now, rearranging the equation gives us:
TC=TA+15(TB−TA)
Distributing the 15:
TC=TA+15TB−15TA
Combining like terms:
TC=55TA−15TA+15TB
TC=45TA+15TB
Step 8: Final Expression for TC
Thus, we can express TC as:
TC=4TA+TB5
Conclusion
The tension in the rope at a distance L5 from end A is:
TC=4TA+TB5
We have a uniform rope with mass M and length L. The tension at end A is TA and at end B is TB, where TB>TA. We need to find the tension TC at a point C which is located at a distance L5 from end A.
Since the tension increases from TA to TB, there must be a net force acting on the rope, which implies that the rope is accelerating. We can write the equation for the net force acting on the entire rope:
Now, let's focus on the segment of the rope from point A to point C (length L5). The mass of this segment can be calculated as:
For the segment from A to C, we can write the force equation as follows:
From Step 2, we have A=TB−TAM. Substitute this expression for A into the equation from Step 4:
This simplifies to:
Now, rearranging the equation gives us:
Thus, we can express TC as:
The tension in the rope at a distance L5 from end A is:
Topper's Solved these Questions
Similar Questions
A uniform rope of length L is pulled by a constant force F. What is the tension in the rope at a distance l from the end where it is applied?
View SolutionA uniform rope of length L is pulled by a constant force F. What is the tension in the ropww at a distance l from the end where it is applied?
View Solution
Knowledge Check
A perfectly straight portion of a uniform rope has mass M and length L . At end A of the segment, the tension in the rope is TA and at end B it is TB(TB>TA . Neglect effect of gravity and no contact force acts on the rope in between points A and B . The tension in the rope at a distance L/5 from end A is.
ATB−TAB(TA+TB)/5C(4TA+TB)/5D(TA−TB)/5A straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'l' from that end is
AFlBLFlC(1−lL)FD(1+lL)FA rope of length 5 m is kept on frictionless surface and a force of 5 N is applied to one of its end. Find the tension in the rope at 1 m from this end
A1 NB3 NC4 ND5 N
A uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
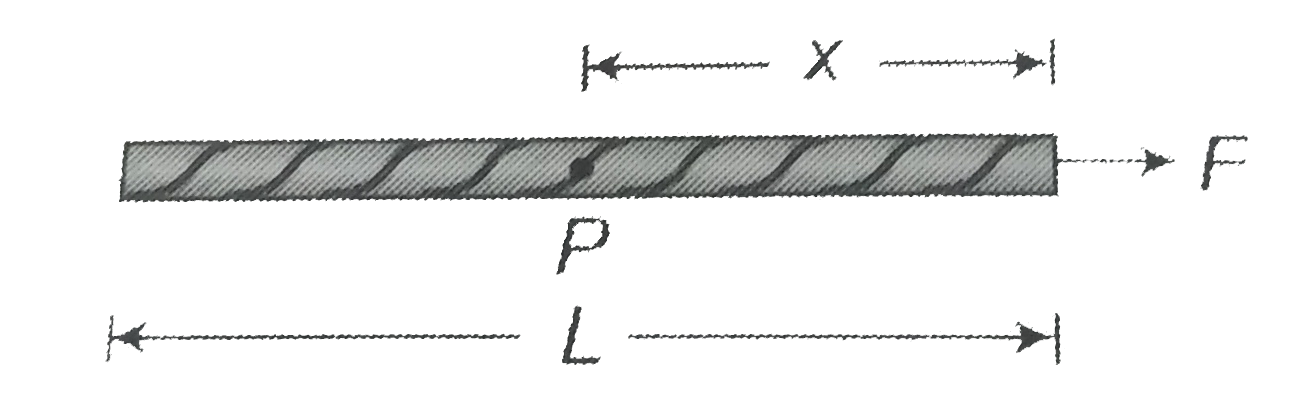
View SolutionA uniform rope of mass m and length L is attached to the ceiling of a lift. The other end of the rope is attached to a block of mass M. The lift is moving up with a constant acceleration a0. Find the tension in the rope at a distance x from the ceiling as shown in the diagram.

View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'I from that end is 9
View SolutionA pulse is generated at lower end to a hanging rope of uniform density and length L. The speed of the pulse when it reaches the mid point of rope is
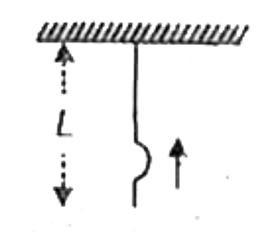
View SolutionA rope of length 20 cm is kept on frictionless surface and a force of 5 N is applied to one of its end. Find the tension in the rope at 5m from this end.
View Solution
