चित्र 21.W.3 में एक चिरनी दिखाई गई है जिसका द्रव्यमान m है तथा अपने अक्ष के प्रति जड़त्व आघूर्ण I है। घिरनी पर से एक डोरी जा रही है जिसका एक सिरा छत से और दूसरा सिरा एक स्प्रिंग से बंधा हुआ है। स्प्रिग का दूसरा सिरा छत में जड़ा हुआ है। घिरनी के केंद्र की सरल आवर्त गति का आवर्तकाल ज्ञात कीजिए । स्प्रिंग का स्प्रिग नियतांक है तथा डोरी घिरनी पर नहीं फिसलती है
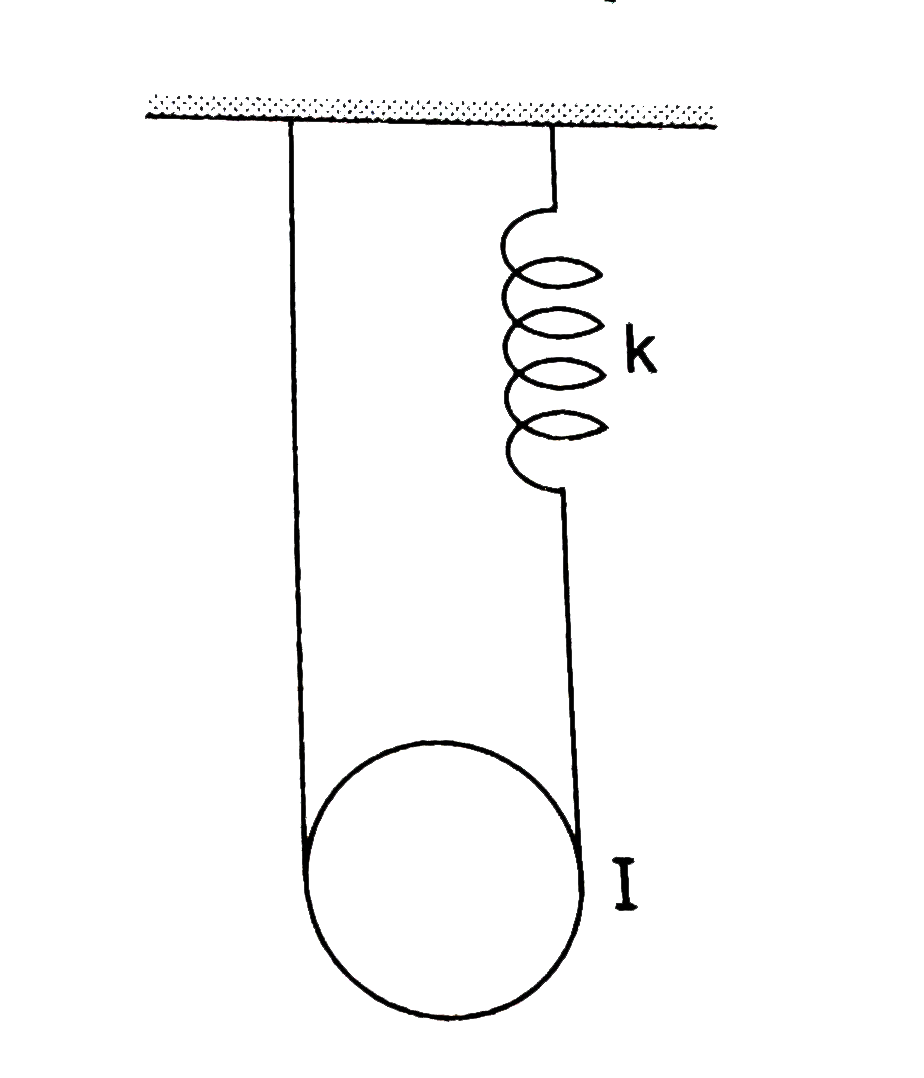
हल सबसे पहले हम साम्यावस्था में स्प्रिंग का तनाव ज्ञात करते हैं। घिरनी की घूर्णन साम्यावस्था के लिए घिरनी के दोनों ओर की डोरियों में तनाव समान होना चाहिए। केवल तभी घिरनी पर बल आघूर्ण शून्य होगा
मान ले कि तनाव T है। स्प्रिंग में भी तनाव उतना ही होगा जितना डोरी में है। अतः साम्यावस्था के लिए स्प्रिंग की लंबाई में वृद्धि Y=Tk
घिरनी की स्थानांतरीय साम्यावस्था के लिए,
2T=mg या 2ky=mg या mg2k
अतः, जब घिरनी साम्यावस्था में होती है, उस समय स्प्रिंग अपनी स्वाभाविक लंबाई वाली स्थिति से mg2k लंबाई नीचे रहता है।
अब मान ले कि किसी क्षण घिरनी का केंद्र साम्यावस्था रो नीचे को ओर दूरी । पर है। ऐसी स्थिति में डोरी + स्प्रिग की कुत लबाई में वृद्धि 2x है (घिरनी की दायी और तथा बाया और x)। चूंकि डोरी की लंबाई रिथर है, अतः स्प्रिंग की लंबाई में वृद्धि 2x है। इस क्षण निकाय की ऊर्जा है
U=12Iω2+12mv2−mgx+12k(mg2k+2x)2
=12(1r2+m)v2+m2g28k+2kx2
चूकि इस पूरी संहति में कहीं भी ऊर्जा का क्षय नहीं हो रहा है,
dVdt=0
अतः 0=(1r2+m)vdvdt+4kxv
या (dv)=−4kx(1r2+m)
a=−ω2x,ω2=4k(Ir2+m)
घिरनी का द्रव्यमान केंद्र एक सरल आवर्त गति करता है जिसका आवर्तकाल,
T=2π√(Ir2+m)/(4k)
Topper's Solved these Questions
- सरल आवर्त गति Book:HC VERMA HINDIChapter:सरल आवर्त गति Exercise:विचार हेतु प्रश्न
Explore 8 Videos
- सरल आवर्त गति Book:HC VERMA HINDIChapter:सरल आवर्त गति Exercise:सटीक उत्तर वाले प्रश्न I
Explore 18 Videos
- सरल आवर्त गति Book:HC VERMA HINDIChapter:सरल आवर्त गति Exercise:अभ्यास के प्रश्न
Explore 31 Videos
- समतल में गति Book:HC VERMA HINDIChapter:समतल में गति Exercise:अभ्यास के प्रश्न
Explore 21 Videos
- सरल आवर्त गति पर आधारित अन्य गतियाँ Book:HC VERMA HINDIChapter:सरल आवर्त गति पर आधारित अन्य गतियाँ Exercise:अभ्यास के प्रश्न
Explore 8 Videos
Similar Questions
एक ब्यक्ति दिन भर काम करके प्रतिदिन ठीक रात्रि 10 बजे बिस्तर पर सौ जाता है। क्या यह आवृति गति का उदाहरण है? यदि ही, तो आवर्तकाल कितना है? यादि नहीं, तो क्यों?
View Solutionएक विद्यार्थी दाबा करता है कि उसने किसी कम पर बल लगाया है तथा कण सरल आवर्त गाति वह यह बलाने से मना कर रहा है कि नियत है या नही। मान ले कि उसका वकतय x के केवल धनात्मक मानों के लिए हो है तथा कम पर अन्य कोई बल कार्यरत नहीं है. तो
View Solutionमूलबिंदु को मध्यबिंदु बनाकर -अक्ष पर सरल आवर्त गति करते एक कण का आयाम 10cm तथा आवर्तकाल 6s है।t=0 समय पर इसकी स्थिति =5cm है तथा यह अक्ष की धनात्मक दिशा में चल रहा है। t समय पर इसके विस्थापन के लए समीकरण लिखे।t = 4s समय पर कण के त्वरण का परिमाण निकालें
View Solutionएक मनुष्य को एक पार्क में जाने के लिए अपने घर से 50 m उत्तर , फिर 40 m पूर्व ओर फिर 20 m दक्षिण जाना पड़ता है । (a ) उसे अपने घर से पार्क तक पहुँचने में कितनी दुरी चलनी पड़ती है ? (b ) घर से पार्क तक के विस्थापन का परिमाण बताएं ।
View Solutionएक कण को एकसाथ दो आवर्त गतियाँ प्रदान की जाती है जिसकी दिशाएँ समान है तथा आवर्तकाल भी सामान हैं। एक का आयाम 3.0 cm तथा दूसरे का आयाम 4.0 cm है। परिणामी गति का आवर्तकाल निकालें यदि दोनों के बीच का कलांतर (a)0∘(b)60∘ तथा (c)90∘ हो।
View Solution22 मी. × 20 मी. आयताकार छत से एक बेलनाकार पात्र जिसका व्यास 2 मी. तथा ऊंचाई 3.5 मी. है में पानी गिरता है। यदि पात्र पूरा भरा हुआ हो तब होई हुई वर्षा (सेमी. में) में ज्ञात करें?
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solution30 सेमी लम्बी एक छड़ AB दो लम्ब अक्षो पर इस प्रकार फिसलती है की छड़ का एक सिरा एक अक्ष पर एक दूसरा सिरा दूसरे अक्ष पर रहता है । छड़ के बिंदु C का बिन्दुपथ ज्ञात कीजिए जिससे AC तथा BC का अनुपात 2:1 रहे ।
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionनिम्नांकित में से कौन-सा निबंध का एक भाग है?
View Solutionनिम्नांकित में से कौन-सा.निबंध का एक भाग है,?
View Solution

