दो संकेद्रीय गोलीय कोशों के द्रव्यमान m1,m2 एवं त्रिज्याऍं R1,R2 (R_(1) lt R_(2)) है। केद्र से (R1+R22)दूरी पर m द्रव्यमान का एक कण रखा है। इस कण पर गोलो के कारण लगनेवाला कुल बल कितना होगा।
4GM1m(R1+R2)2
Topper's Solved these Questions
- गुरुत्वाकर्षण Book:HC VERMA HINDIChapter:गुरुत्वाकर्षण Exercise:सटीक उत्तरवाले प्रश्न II
Explore 6 Videos
- कोणीय सरल आवर्त गति Book:HC VERMA HINDIChapter:कोणीय सरल आवर्त गति Exercise:अभ्यास के प्रश्न
Explore 20 Videos
- गोलीय सतहों पर अपवर्तन Book:HC VERMA HINDIChapter:गोलीय सतहों पर अपवर्तन Exercise:अभ्यास के प्रश्न
Explore 50 Videos
Similar Questions
किसी बिंदु पर गुरूत्वीय विभव एवं गुरूत्वीय क्षेत्र क्रमश: V तथा E है। ऐसा हो सकता है कि
View Solutionजिस दोलक का आवर्तकाल 2 सेकण्ड हो, तो उसे सेकण्ड दोलक कहते हैं। पहले के ज़माने में बहुत -सी घड़ियाँ इसी प्रकार के दोलकों से बनती थी। यदि g का मान π2m/s2 हो, तो सेकण्ड दोलक को लम्बाई निकालें।
View Solutionचित्र में दिखाई गई सतह के दाहिने काँच ( n = 1.5) तथा बाएँ हवा हैं । सतह की त्रिज्या 20 cm हैं तथा उससे 25 cm दूरी पर हवा में एक बिंदुस्त्रोत रखा हैं । प्रतिबिंब का स्थान बताएँ ।
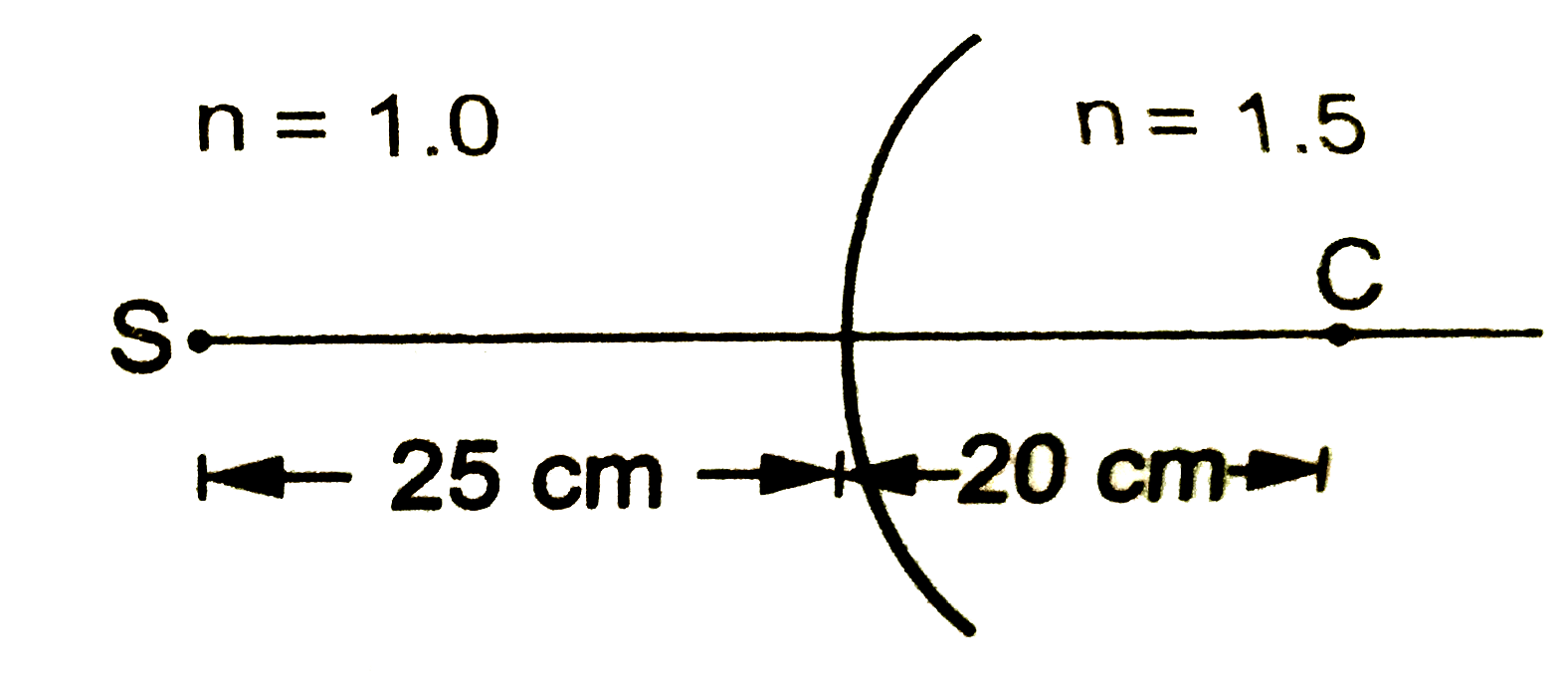
View SolutionTwo planets of radii R_(1) and R_(2 have masses m_(1) and M_(2) such that (M_(1))/(M_(2))=(1)/(g) . The weight of an object on these planets is w_(1) and w_(2) such that (w_(1))/(w_(2))=(4)/(9) . The ratio R_(1)/R_(2)
View SolutionThe figure represents two concentric shells of radii R_(1) and R_(2) and masses M_(1) and M_(2) respectively. The gravitational field intensity at the point A at distance a (R_(1) lt a lt R_(2)) is
View SolutionTwo concentric spherical shells have masses m1, m2 and radit R1,R2(R1<R2). Calculate the force by this system on a particle of mass m, if it is placed at a distance (R1+R2)2 from the centre.
View SolutionSupposing Newton's law of gravitation for gravitation force F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F2=−F2=r12r312GM20(m1m2M20)n where M0 is a constant dimension of mass, r12=r1−r2 and n is number. In such a case.
View SolutionTwo concentric spherical shells have masses m_(1) and m_(2) and radii r_(1) and r_(2) (r_(2) gt r_(1)) . What is the force exerted by this system on a particle of mass m_(3) . If it is placed at a distance r(r_(1) lt r lt r_(2)) from the centre ?
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View SolutionStatement I In a ΔABC,ifa<b<c and ri si inradius and r1,r2+r2r3 are the exradii opposite to angle A,B,C respectively, then r<r1<r2<r3.
Statement II For, ΔABCr1r2+r2r3+r3r1=r1r2r3r
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!2
View SolutionIn a ΔABC, if 2r2r3r2−r1=r3−r1 then
r1(r2+r3)√r1r2+r2r3+r3r1=
View SolutionTwo planets of radii R1 and R2 have masses m1 and M2 such that M1M2=1g. The weight of an object on these planets is w1 and w2 such that w1w2=49. The ratio R1R2
View SolutionTwo concentric spherical shells have masses M1,M2 and radii R1,R2(R1<R2). The force exerted by this system on a particle of mass m. If it is placed at a distance (R1+R22) from the centre.
View Solution

