Two planets of radii R1 and R2 have masses m1 and M2 such that M1M2=1g. The weight of an object on these planets is w1 and w2 such that w1w2=49. The ratio R1R2
2
12
4
14
The correct Answer is:B
Step by step video, text & image solution for Two planets of radii R_(1) and R_(2 have masses m_(1) and M_(2) such that (M_(1))/(M_(2))=(1)/(g). The weight of an object on these planets is w_(1) and w_(2) such that (w_(1))/(w_(2))=(4)/(9). The ratio R_(1)/R_(2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two planets of radii r1 and r2 are made from the same material. The ratio of the acceleration of gravity g1/g2 at the surfaces of the planets is
View SolutionConsider two solid sphere oFIGURE radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitional FIGUREield due to sphere 1 and 2 are shown. The value oFIGURE M1M2) is:
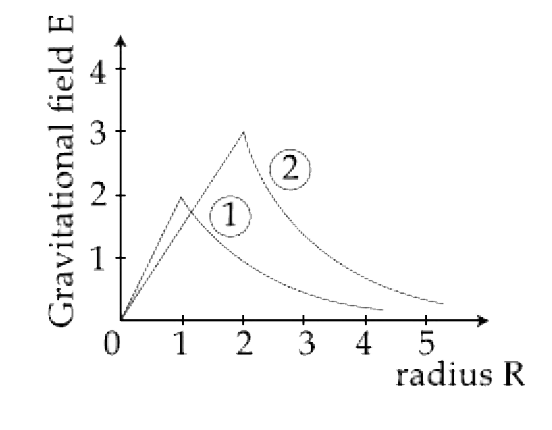
View Solution
Knowledge Check
If two planets of radii R1andR2 have densities d1andd2, then the ratio of their respective acceleration due to gravity is
AR1d1:R2d2BR21d1:R22d2CR31d1:R32d2DR1d21:R22d22Two planets have radii r1andr2 and densities d1andd2 respectively. Then the ratio of acceleration due to gravity on them is
Ar1d1:r2d2Br1d2:r2d1Cr21d1:r22d2Dr22d1:r21d2Two planets have radii r1and2r1 and densities are ρ1and4ρ1 respectively. The ratio of their acceleration due to gravities is
A1:8B8:1C4:1D1:4
Consider two solid spheres of radii R1=1m,R2=2m and masses M1andM2 , respectively . The gravitational field due to sphere (1) and (2) are shown. The value of M1M2 is :
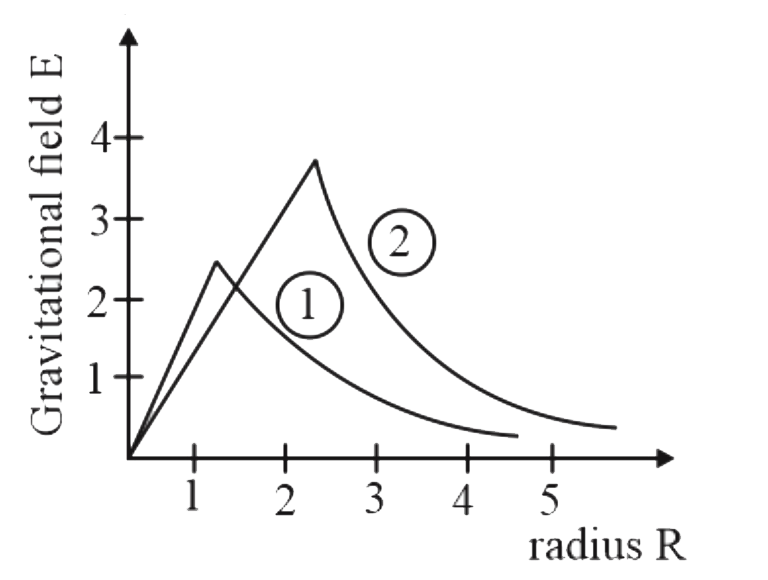
View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View SolutionTwo spherical nuclei have mass number 216 and 64 with their radii R1andR2 respectively. The ratio, R1R2 is equal to
View SolutionThree planets of same density have radii R1,R2 and R3 such that R1=2R2=3R3. The gravitational field at their respective surfaces are g1,g2 and g3 and escape velocities from their surfeces are υ1,υ2 and υ3, then
View SolutionTwo particles of masses m1andm2 are moving in concentric circle of radii r1andr2 such that their period are same. Then the ratio of their centripetal acceleration is
View Solution
