एक समरूप ठोस गोले का द्रव्यमान M तथा त्रिज्या r है। इसे $\frac{v_{0}}{2 r}$ कोणीय वेग से अपने एक व्यास के परितः घुमाया जाता है तथा $v_{0}$ रेखीय वेग से एक क्षैतिज तल पर चला दिया जाता है (चित्र 19.7W) । तल द्वारा लगाए गए घर्षण बल के कारण गोले का रेखीय वेग तथा इसके कोणीय वेग बदलते है और अंत में वह शुद्ध लोटनी गति करने लगता है। इस अवस्था में गोले का रेखीय वेग निकालें। सतहों के विरूपण को अनदेखा करे।

Video Solution

Text Solution

Verified by Experts

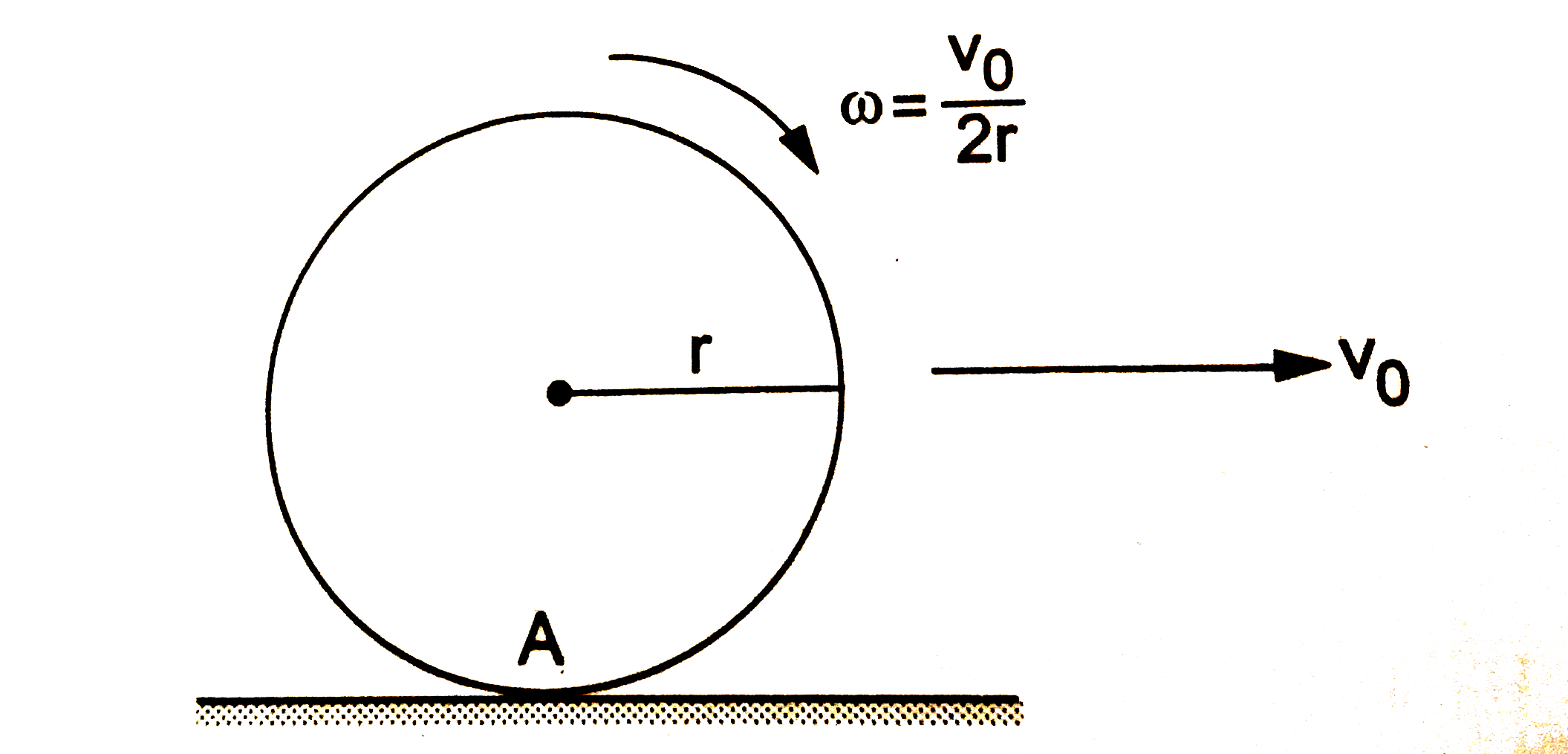
पहली विधि-
प्रांरभ में गोले का कोणीय वेग, $ω_{0} = \frac{v_{0}}{2 r}$
या $ω_{0} r = \frac{v_{0}}{2} < v_{0}$
अतः, सपंर्क पर गोले की सतह क्षैतिज सतह पर आगे की ओर फिसलेगी और गोले पर घर्षण पीछे की ओर लगेगा। चूँकि यह गतिज घर्षण है,
$f = μ N = μ M g$
अतः, गोले के केंद्र का त्वरण $a = \frac{f}{M} = μ g$
समय t पर गोले के केंद्र का वेग,
$v (t) = v_{0} - μ gt ... ... . (i)$
इस घर्षण बल का बल-आघूर्ण $= μ M g r$ तथा गोले का जड़त्व आघूर्ण $= \frac{2}{5} M r^{2}$
अतः, गोले का कोणीय त्वरण,
$α = \frac{τ}{I} = \frac{μ M g r}{\frac{2}{5} M r^{2}} = \frac{5 μ g}{2 r}$
यह कोणीय त्वरण गोले का कोणीय वेग को बढ़ाएगा। t समय में गोले का कोणीय वेग,
$ω (t) = ω_{0} + α t = \frac{v_{0}}{2 r} + \frac{5 μ g}{2 r} t$
या $r ω (t) = \frac{v_{0}}{2} + \frac{5 μ gt}{2} ... ... (i i)$
गोले का फिसलना तब बंद होगा, जब $6 v (t) = r ω (t)$ समीकरण (i) तथा समीकरण (ii) से, $v_{0} - μ gt = \frac{v_{0}}{2} + \frac{5 μ g}{2} t$
या $μ gt = \frac{v_{0}}{7}$
समीकरण (i) से
$v (t) = v_{0} - \frac{v_{0}}{7} = \frac{6}{7} v_{0}$ .
दूसरी विधि
प्रारंभ में क्षैतिज तल पर गोले के संपर्क-बिंदु A के प्रति बल-आघूर्ण पर विचार करे। किसी भी समय घर्षण की क्रियारेखा सी बिंदु से गुजरती है। अतः, घर्षण बल का बल-आघूर्ण A के प्रति शून्य है। भार तथा अभिलंब बल, एक ही रेखा पर, बराबर तथा विपरीत दिशा में है, अतः उनका भी कुल बल-आघूर्ण A के प्रति शून्य है। अतः, बिंदु A के प्रति गोले का कोणीय संवेग गति के दौरान नहीं बदलेगा। A से जानेवाली चित्र के तल के लंबवत रेखा के प्रति कोणीय संवेग की गणना करे।
$\to L = {\to L}_{C M} + M \to R \times \to v$
प्रारंभिक कोणीय संवेग,
$L_{z} I_{C M} ω_{0} + M r v_{0}$
$= (\frac{2}{5} M r^{2}) (\frac{v_{0}}{2 r}) + M r v_{0} = \frac{6}{5} M r v_{0}$
जब गोले का फिसलना बंद हो जाता है तब उसका वेग v तथा कोणीय वेग v/r हो जाता है। इसी रेखा के प्रति अंतिम कोणीय संवेग
$= (\frac{2}{5} M r^{2}) (\frac{v}{r}) + M r v = \frac{7}{5} M r v ।$
चूँकि इस रेखा के प्रति संवेग नहीं बदलता, अतः
$= \frac{6}{5} M r v_{0} = \frac{7}{5} M r v या v = \frac{6}{7} v_{0}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS मिश्र - स्थानांतरित - घूर्णन गति

Topper's Solved these Questions

Similar Questions

HC VERMA HINDI-मिश्र - स्थानांतरित - घूर्णन गति -हल किए गए प्रश्न

Home
Ask Doubt
Profile