दो बेलनाकार वस्तुएँ अपने-अपने अक्ष के परितः ω1 तथा ω2 कोणीय गेव से घूर्णन कर रही है। इनकी त्रिज्याएँ r1 तथा r2 है और अपने अक्षो के प्रति इनके जड़त्व आघूर्ण I1 तथा I2 है। अब दोनों वस्तुओ को अपने अक्ष के समानांतर खिसकाते हुए पास-पास लाया जाता है, ताकि उनकी सतहे एक-दूसरे को स्पर्श करे (चित्र 19.W3) । संपर्क के स्थान पर वस्तुएँ एक-दूसरे पर फिसलती है और अंत में यह फिसलना बंद हो जाता है। इस समय वस्तुओं के कोणीय वेग निकालें।
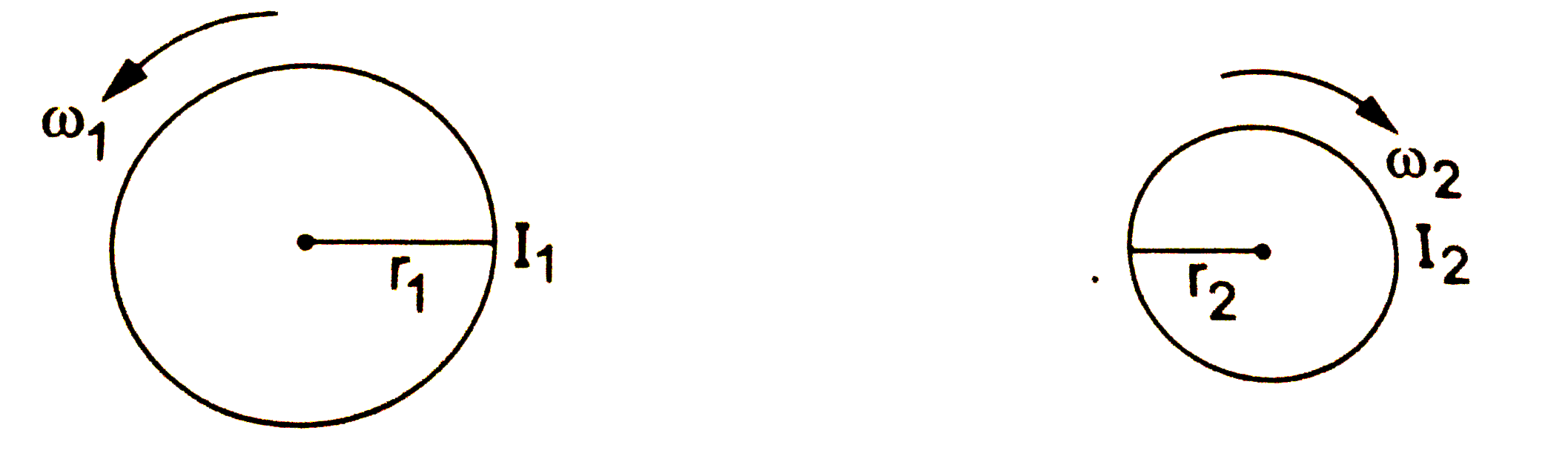
चूँकि दोनों बेलन अलग-अलग अक्षो के प्रति घूम रहे है, कोणीय संवेग संरक्षण का उपयोग करना कठिन है। जब फिसलना बंद होगा, तब संपर्क पर स्थित दोनों सतहों के रेखीय वेग बराबर होंगे।
जिस समय वस्तुएँ एक-दूसरे से सटती है, पहली वस्तु के संपर्क भाग का वेग v1=ω1r1 तथा दूसरी वस्तु के संपर्क भाग का वेग v2=ω2r2 होगा। मान ले कि v1>v2 है। ऐसी स्थिति में पहले वस्तु की संपर्क सतह दूसरे वस्तु की संपर्क सतह पर (चित्र 19.W4) ऊपर की ओर फिसलेगी। इसलिए, पहली वस्तु पर घर्षण का बल f नीचे की ओर लगेगा। इस बल का पहले बेलन के अक्ष के प्रति बल-आघूर्ण fr1 होगा जो इसके कोणीय वेग ω1 को कम करेगा।
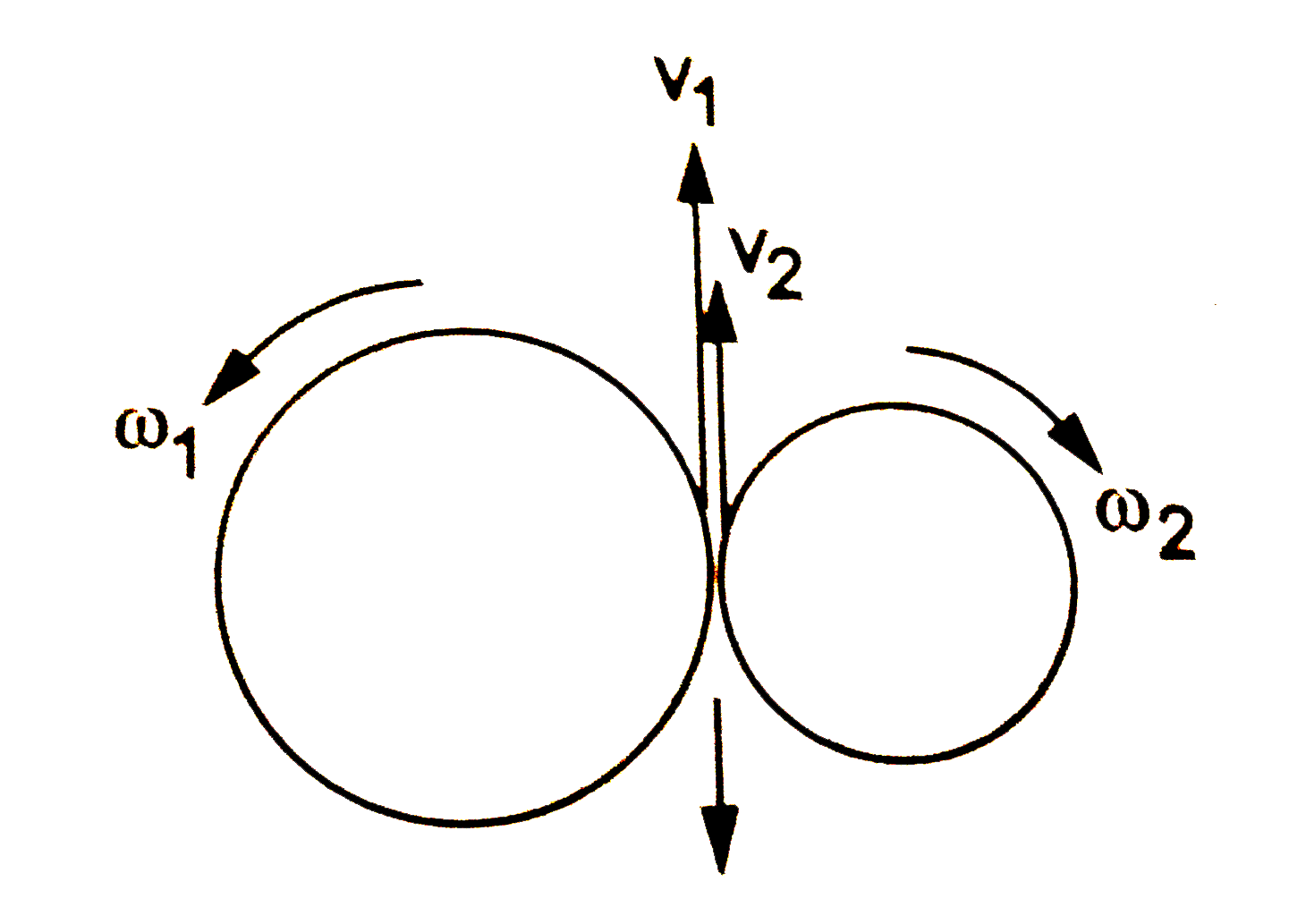
दूसरी वस्तु पर घर्षण बल ऊपर की ओर लगेगा (चित्र 19.W4) तथा इसका परिमाण f ही होगा। इस बल का दूसरे बेलन के अक्ष के प्रति बल-आघूर्ण fr2 होगा जो इसके कोणीय वेग ω2 को बढ़ाएगा। यह प्रक्रिया तब तक चलती रहेगी जब तक कि संपर्क सतहों पर दोनों वस्तुओ के रेखीय वेग बराबर न हो जाएँ। मान ले कि इस स्थिति में इनके कोणीय वेग ω1' तथा ω2' हो जाते है और इस स्थिति तक आने में t समय लगता है।
तब पहली वस्तु के लिए,
fr1=I1ω1'−ω1't ......(i) तथा दूसरी वस्तु के लिए,
fr2=I2ω2'−ω2't ......(ii)
साथ ही, ω1'r1=ω'1r2. .......(iii)
समीकरण तथा समीकरण (ii) से f को विलुप्त करने पर,
r1r2=I1(ω1−ω'1)I2(ω'2−ω2). ......(iv)
समीकरण (iii) तथा समीकरण (iv) को हल करने पर,
ω'1=I1ω1r2+I2ω2r1I2r21+I1r22 तथा ω'2=I1ω1r2+I2ω2r1I2r21+I1e22r1.
Topper's Solved these Questions
- मिश्र - स्थानांतरित - घूर्णन गति Book:HC VERMA HINDIChapter:मिश्र - स्थानांतरित - घूर्णन गति Exercise:विचार हेतु प्रश्न
Explore 5 Videos
- मिश्र - स्थानांतरित - घूर्णन गति Book:HC VERMA HINDIChapter:मिश्र - स्थानांतरित - घूर्णन गति Exercise:सटीक उत्तरवाले प्रश्न I
Explore 7 Videos
- मिश्र - स्थानांतरित - घूर्णन गति Book:HC VERMA HINDIChapter:मिश्र - स्थानांतरित - घूर्णन गति Exercise:अभ्यास के प्रश्न
Explore 20 Videos
- मापन की संभावित त्रुटियाँ एवं सार्थक अंक Book:HC VERMA HINDIChapter:मापन की संभावित त्रुटियाँ एवं सार्थक अंक Exercise:अभ्यास के प्रश्न
Explore 13 Videos
- लेंस-आधारित उपकरण Book:HC VERMA HINDIChapter:लेंस-आधारित उपकरण Exercise:अभ्यास के प्रश्न
Explore 26 Videos
Similar Questions
वस्तु की जो गति एक फ्रेम में शुद्ध स्थानांतरीय है, क्या वह किसी दूसरे फ्रेम में शुद्ध घर्षण गति हो सकती है ? क्या यह किसी दूसरे फ्रेम में मिश्र स्थानांतरीय घूर्णन गति हो सकती है ?
View Solutionसमतल सतह पर शुद्ध लोटनी गति कर रहे एक वलय (ring) का केंद्र v0 चाल से गतिशील है। वलय की परिधि पर स्थित उन कणों पर विचार करे जिनकी ऊँचाई सतह से उतनी ही है, जितनी वलय के केंद्र की है। इन कणों की चाल होगी
View Solutionएक बेलन एक क्षैतिज तल पर बिना फिसले लुढ़क रहा है। यदि द्रवमान केंद्र की चाल 25 m/s हो, तो शीर्षतम बिंदु की चाल कितनी होगी ?
View Solutionसंख्या 1001 में कितने सार्थक ( significant ) अंक है ?
View Solutionएक मनुष्य खुले स्थान में चार अलग-अलग वृक्षों को देखता है जिनकी ऊँचाइयाँ तथा दूरियाँ नीचे दी गई है। इन वृक्षों को उनकी आभासी ऊँचाइयों के घटते क्रम में लगाएँ।

View Solutionk के किस मान के लिए रेखाएँ y=(2+√3)x+4 तथा y=kx+6 एक दूसरे से 60∘ के कोण पर झुकी है ?
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solution30 सेमी लम्बी एक छड़ AB दो लम्ब अक्षो पर इस प्रकार फिसलती है की छड़ का एक सिरा एक अक्ष पर एक दूसरा सिरा दूसरे अक्ष पर रहता है । छड़ के बिंदु C का बिन्दुपथ ज्ञात कीजिए जिससे AC तथा BC का अनुपात 2:1 रहे ।
View Solutionएक फैक्टरी दो पदार्थो A और B का निर्माण करती है|पदार्थ A के निर्माण हेतु एक मशीन को 1 .5 घंटे तथा साथ ही एक मिस्त्री को 2 घंटे कार्य करना पढता है|पदार्थ B के निर्माण हेतु मशीन को 2 .5 घंटे तथा मिस्त्री को 1 .5 घण्टे कार्य करना पढता है| प्रति सप्ताह फैक्टरी मशीन को 80 घंटे तथा कारीगरी को 70 घंटे उपलब्ध करात्ती है| प्रत्येक पदार्थ A पर लाभ रु 5 तथा प्रत्येक पदार्थ B पर लाभ रु 4 है| यदि निर्मित सभी पदार्थ बिक जाएँ तो ज्ञात कीजिए की प्रति सप्ताह अधिकतम लाभ के लिए प्रत्येक प्रकार के कितने पदार्थ बनाये जाएँ ?
View Solutionएक उद्यमी दो प्रकार के लैंप A और B बनाता है| लैंप दो कारीगरों (i ) काटने वाले(ii ) निखारने वाले के पास जाते है| लैंप के लिए पहले कारीगर को 2 घंटे लगते है और दूसरे को 1 घंटा लगता है| लैंप B के लिए पहले कारीगर को 1 घंटा लगता है तथा दूसरे को 2 घंटे लगते है| पहले व दूसरे कारीगर के पास कंपनी का करने के लिए प्रति माह क्रमशः 100 घंटे व 80 घंटे उपलब्ध है| लैंप A पर रु 7 तथा B पर रु 11 लाभ होता है| यदि यह मान लिया जाए की जितना माल तैयार होता है| कम्पनी सभी बेच देती है|| तो अधिकतम लाभ के लिए कम्पनी दोनों प्रकार के कितने लैम्प तैयार करेगी?
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
View Solutionदीर्घवृत्त 3x2+5y2=32 के बिंदु P (2,2) पर खींची गई स्पर्श रेखा तथा अभिलम्ब, X-अक्ष को क्रमश: Q तथा R पर काटते है, तो ΔPQR का क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solution
