A→ Product, [A]0=2M. After 10min reaction is 10% completed. If d[A]dt=k[A], then t1/2 is approximately
0.693min
69.3min
66.0min
0.0693min
The correct Answer is:C
To solve the problem step by step, let's break it down:
Step 1: Understand the Given Information
- Initial concentration, (A)0=2M
- The reaction is 10% complete after 10 minutes.
- The rate law is given as d(A)dt=k(A), indicating a first-order reaction.
Step 2: Determine the Concentration After 10 Minutes
Since the reaction is 10% complete, this means that 10% of the initial concentration has reacted. Therefore:
Concentration of A after 10 minutes=(A)=(A)0−0.1(A)0=2M−0.2M=1.8M
Step 3: Use the Integrated Rate Law for First-Order Reactions
For a first-order reaction, the integrated rate law is given by:
ln((A)0(A))=kt
Substituting the known values:
- (A)0=2M
- (A)=1.8M
- t=10minutes
We can write:
ln(21.8)=k⋅10
Step 4: Calculate k
First, calculate 21.8:
21.8≈1.1111
Now, take the natural logarithm:
ln(1.1111)≈0.1054
Now, substitute back to find k:
0.1054=k⋅10⟹k=0.105410≈0.01054min−1
Step 5: Calculate the Half-Life t1/2
For a first-order reaction, the half-life is given by:
t1/2=0.693k
Substituting the value of k:
t1/2=0.6930.01054≈65.7minutes
Conclusion
Thus, the approximate half-life t1/2 is about 66 minutes.
---
- Initial concentration, (A)0=2M
- The reaction is 10% complete after 10 minutes.
- The rate law is given as d(A)dt=k(A), indicating a first-order reaction.
Since the reaction is 10% complete, this means that 10% of the initial concentration has reacted. Therefore:
Concentration of A after 10 minutes=(A)=(A)0−0.1(A)0=2M−0.2M=1.8M
For a first-order reaction, the integrated rate law is given by:
ln((A)0(A))=kt
Substituting the known values:
- (A)0=2M
- (A)=1.8M
- t=10minutes
ln(21.8)=k⋅10
First, calculate 21.8:
21.8≈1.1111
Now, take the natural logarithm:
ln(1.1111)≈0.1054
Now, substitute back to find k:
0.1054=k⋅10⟹k=0.105410≈0.01054min−1
For a first-order reaction, the half-life is given by:
t1/2=0.693k
Substituting the value of k:
t1/2=0.6930.01054≈65.7minutes
Thus, the approximate half-life t1/2 is about 66 minutes.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Assertion-Reasoning
22 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Integer
15 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Multiple Correct
34 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRYCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
Consider the reaction : A→B+C. Initial concentration of A is 1 M. 20 minutes time is required for completion of 20% reaction. If d[B]dt=k[A], then calculate half life (t1/2) of reaction.
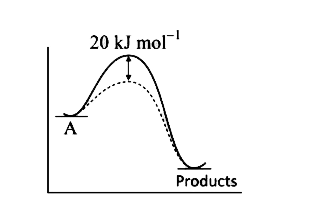
View SolutionFor the following reaction,
A500K−−→ Products
A400K/catalyst−−−−−−−−→ Product
If (−d[A]dt)500K=−(d[A]dt)400K
no catalyst in presence of catalyst Then Ea is approximately :
View Solution
Knowledge Check
A→ Product, [A]0=2M. After 10 min reaction is 10% completed. If d[A]dt=k[A], then t1/2 is approximately
A0.693 minB69.3 minC66.0 minD0.0693 minA reaction of first-order completed 90% in 90 minutes, hence, it is completed 50% in approximately :
A50 minB54 minC27 minD62 minA first order reaction is 10% complete in 20 min. the time taken for 19% completion is :
A30 minB40 minC50 minD38 min
A first order reaction is 20% completed in 10min, (70+h) min it take to complete 80% .What is h? (approximately) (log1.25=0.0969 )
View SolutionFor zero order reaction :
A+2B→Product
If initial concentration of A is 2a and rate law.
−dBdt=K[A]o[B]o
then t1/2 of A will be
View SolutionFor a reation: A→ Product,
rate law is −d[A]dt=K[A]0.
The concentration of A left after time t when t=1K is:
View SolutionIn the reaction 3A→2B, rate of reaction +d[B]dt is equal to :
View SolutionFor a reation: A→ Product,
rate law is −d[A]dt=K[A]0.
The concentration of A left after time t when t=1K is:
View Solution