P is a point on the side BC off the ΔABC and Q is a point such that PQ is the resultant of AP,PB and PC. Then, ABQC is a
square
rectangle
parallelogram
trapezium
The correct Answer is:C
AP+PB+PC=PQ or AP+PB=PQ+CP
⇒AB=CQ
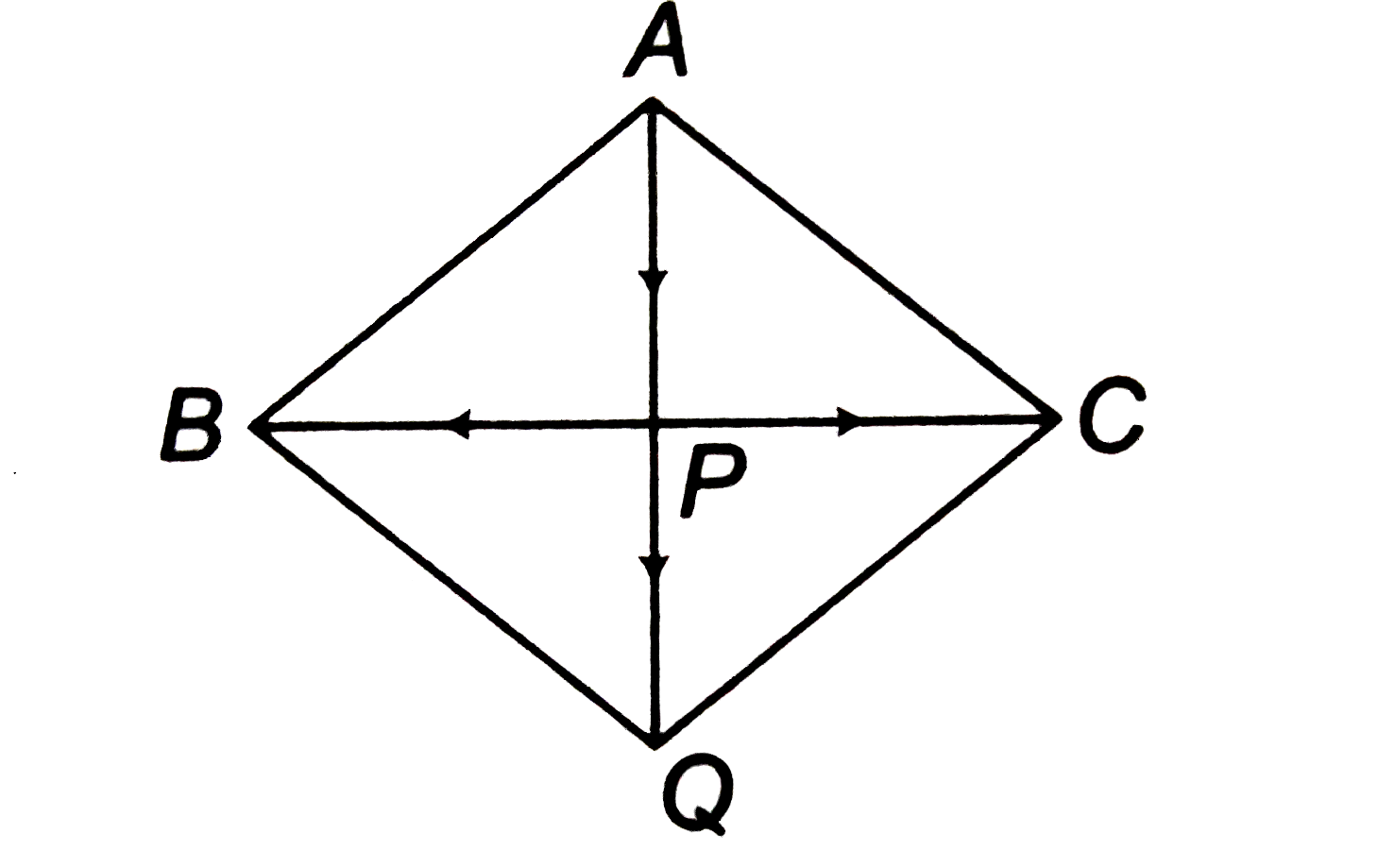
Hence, it is a parallelogram.
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 1
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 2
Explore 17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
Knowledge Check
D is a point on the side BC of a ΔABC such that AD bisects ∠BAC . Then
ABD=CDBBA>BDCBD>BADCD>CAABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
ArectangleBsquareCparallelogramDrhombusIf D is the mid-point of the side BC of ΔABCand the area of ΔABD and the area of ΔACD is 16cm2, then the area of ΔABC is
A16cm2B24cm2C32cm2D48cm2
IN any △ABC, a point p is on the side BC. If −−→PQis the resultant of the vectors −−→AP,−−→PB and −−→PC the prove that ABQC is a parallelogram and hence Q is a fixed point.
View SolutionComprehension (Q.6 to 8) A line is drawn through the point P(−1,2) meets the hyperbola xy=c2 at the points A and B (Points A and B lie on the same side of P) and Q is a point on the lien segment AB. If the point Q is choosen such that PQ, PQ and PB are inAP, then locus of point Q is x+y(1+2x) (b) x=y(1+x) 2x=y(1+2x) (d) 2x=y(1+x)
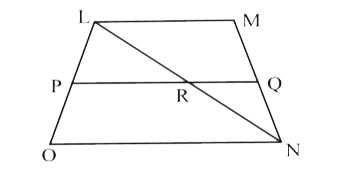
View SolutionIn the figure LMNO, is a trapezium in which LM is parallel to side ON and P is the mid point of side LO. If Q is a point on the side MN such that segment PQ is parallel to side ON Prove that Q is the mid point of MN and PQ=1/2(LM+ON).
View SolutionΔABC is a triangle with the point P on side BC such that 3BP=2PC, the point Q is on the line CA such that 4CQ=QA. Find the ratio in which the line joining the common point R of AP and BQ and the point S divides AB.
View SolutionIn ΔABC, P is a point on BC such that BP : PC = 2 : 3 and Q is the midpoint of BP. Then ar (ΔABQ):ar(ΔABC) is equal to :
View Solution