ΔABC में , AD⊥BC और AD2=BD.CD तो सिद्ध करें कि ∠BAC=90∘
दिया है : एक ΔABC जिसमे AD⊥BC और AD2=BD.CD
सिद्ध करना है : ∠BAC=90∘
उपपत्ति : AD2=BD.CD
⇒BDAD=ADCD ....(i)
अब ΔDBA और ΔDAC में,
∠BDA=∠ADC=90∘ (दिया है)
और BDAD=ADCD
∴ΔDBA~ΔDAC
∴∠B=∠2 और ∠1=∠C
∴∠1+∠2=∠B+∠C
⇒∠A=∠B+∠C
⇒2∠A=∠A+∠B+∠C
⇒2∠A=180∘
⇒∠A=90∘ (प्रमाणित)
Topper's Solved these Questions
- त्रिभुज Book:KC SINHAChapter:त्रिभुज Exercise:EXCERCISE 6.1
Explore 22 Videos
- त्रिभुज Book:KC SINHAChapter:त्रिभुज Exercise:EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
Explore 8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ Book:KC SINHAChapter:त्रिकोणमितीय अनुपात और सर्वसमिकाएँ Exercise:EXERCISE 8.4
Explore 85 Videos
- दो चर वाले रैखिक समीकरण युग्मBook:KC SINHAChapter:दो चर वाले रैखिक समीकरण युग्मExercise:वस्तुनिष्ठ प्रश्न
Explore 44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionIn triangle ABC, if AD perp BC and AD^(2)=BD*DC. Then find the angle BAC
View Solutionमाना कि एक त्रिभुज ABC है जिसमे ∠A=90∘ तथा AD⊥BC तो सिद्ध कीजिए कि AD2=BD⋅CD
View Solutionत्रिभुज ABC में, यदि AD⊥BC तथा AD2=BD×DC हो, तो सिद्ध करो की ∠BAC=90∘|
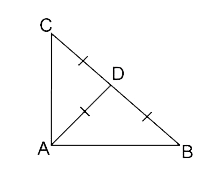
View SolutionIn the given if AD=BD=CD , Find ∠BAC
View SolutionΔABC is a right angled triangle where ∠B=90∘ and BD⊥AC . If BD = 8 cm , AD = 4 cm , then CD is ………..
View SolutionABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then BDCD is equal to :
View SolutionABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then BDCD is equal to :
View SolutionΔABC లో AD⊥BC మరియు AD2=BD∗CD అయిన త్రిభుజము ABC లంబకోణ త్రిభుజామని చూపుము.
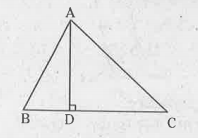
View SolutionIn ΔABC, ∠ABC=90∘, BD⊥AC. If BD=8cm, AD=4cm, find CD .
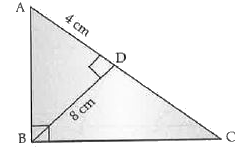
View SolutionIn ΔABC, CD⊥AB, CA=2AD and BD=3AD. Prove that ∠BCA=90∘
View SolutionABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then BDCD is equal to :
View Solution

