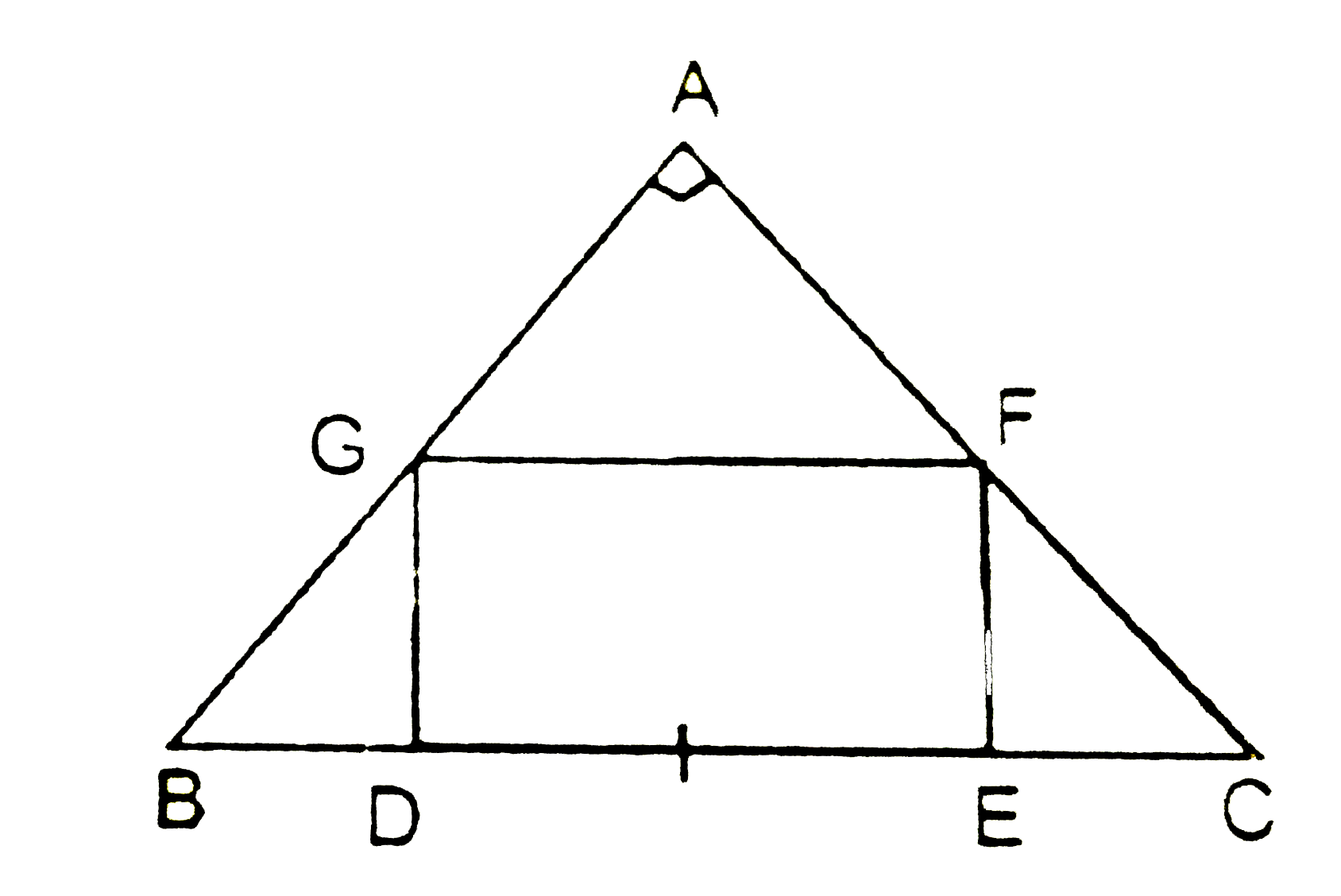
दिए गये चित्र में DEFG एक वर्ग है और ∠BAC=90∘. सिद्ध कीजिए कि :
(i) ΔAGF~ΔDBG
(ii) ΔAFG~ΔEFC
(iii) ΔDBG~ΔEFC
(iv) DE2=DB×EC
दिया है : ABCD एक त्रिभुज है
जिसमे ∠BAC=90∘ और DEFG एक वर्ग है ।
सिद्ध करना है : (i) ΔAGF~ΔDBG
(ii) ΔAFG~ΔEFC
(iii) ΔDBG~ΔEFC
(iv) DE2=DB×EC
उपपत्ति : ΔAGF और (ΔDBGमें,
∠GAF=∠BDG=90∘ (संगत कोण)
∠AGF=∠DBG (∵GF∣BCऔरABतिर्यक रेखा है)
∴ΔAGF~ΔDBG ( A A समरूपता से)
(ii) ΔAGF और ΔEFC में,
∠FAG=∠CEF=90∘
∠GFA=∠FCE ( संगत कोण)
(∵GF∣∣BCऔरACतिर्यक रेखा है)
∴ΔAGF~ΔEFC (AA समरूपता से)
(iii) ΔDBG~ΔAGF और ΔAGF~DetlaEFC में, (ऊपर (i) और (ii) में प्रमाणित)
∴∠DBG=∠EFC
(iv) ΔDBG~ΔEFC
⇒BDFE=DGEC (संगत भुजाएँ समानुपाती है)
⇒BDDE=DEEC (∵DG=DEऔरFE=DEक्योंकिDGEFएक वर्ग है)
अतः DE2=BD×EC
Topper's Solved these Questions
- त्रिभुज Book:KC SINHAChapter:त्रिभुज Exercise:EXCERCISE 6.1
Explore 22 Videos
- त्रिभुज Book:KC SINHAChapter:त्रिभुज Exercise:EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
Explore 8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ Book:KC SINHAChapter:त्रिकोणमितीय अनुपात और सर्वसमिकाएँ Exercise:EXERCISE 8.4
Explore 85 Videos
- दो चर वाले रैखिक समीकरण युग्मBook:KC SINHAChapter:दो चर वाले रैखिक समीकरण युग्मExercise:वस्तुनिष्ठ प्रश्न
Explore 44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionWhich of the following symbols are not acceptable ? (i) ._(35)^(79)Br (ii) .^(79)Br (iii) ._(79)^(35)Br (iv) ._(35)Br
View SolutionConsider the given reaction RCOOAgoverset(Br_(2)//Delta)toR-Br Which one of the following aicd will give maximum yield of R-Br in the above reaction?
View SolutionIn the given figure, DEFG is a square and angle BAC= 90^(@) , Prove that (i) Delta AGF~ Delta DBG (ii) Delta AGF~ Delta EFC (iii) DE^(2)=BDxxEC
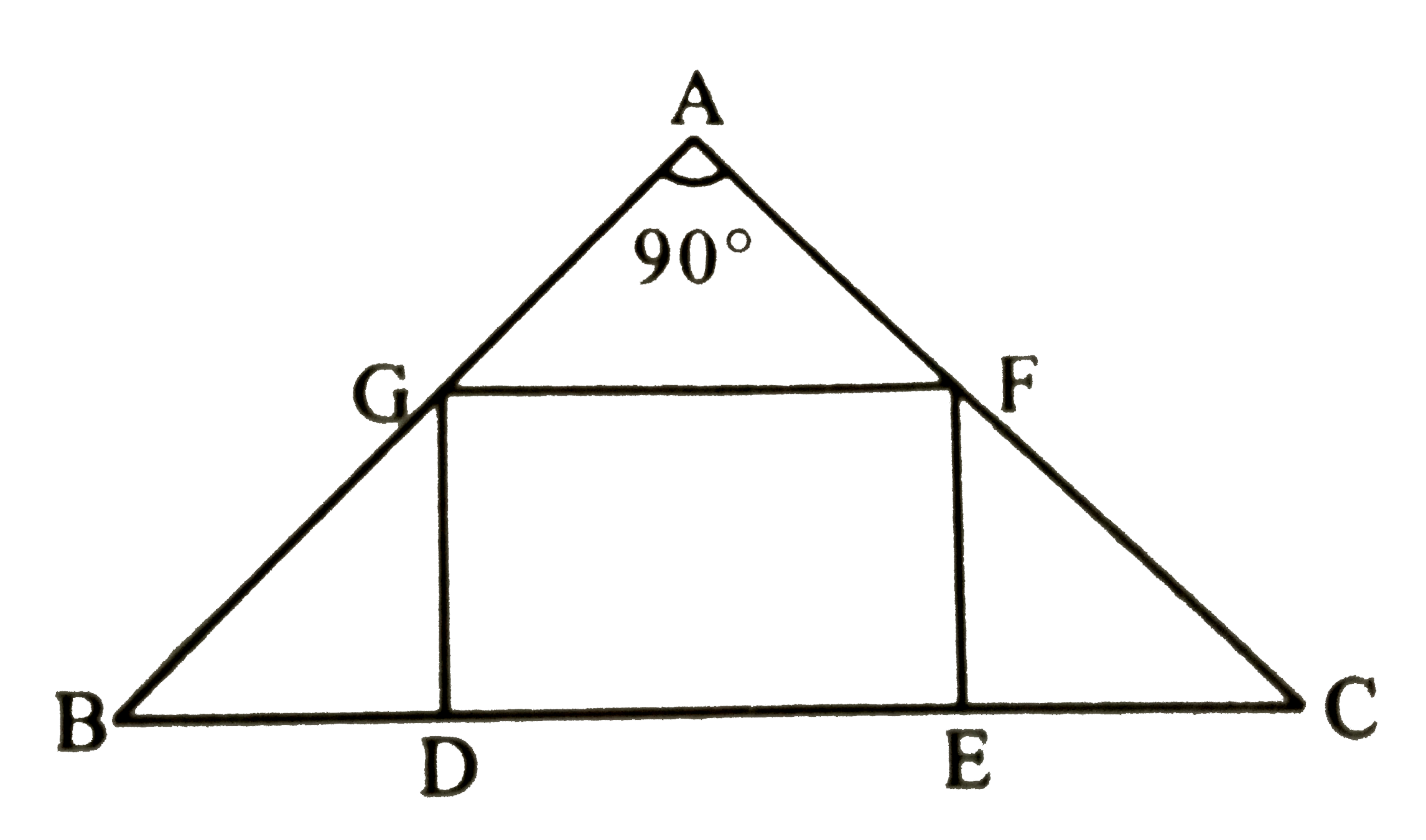
View Solutionदी गई आकृति में, एक वर्ग DEFG है तथा ∠BAC=90∘ है तो सिद्ध कीजिए कि
(i) △AFG~△DBG
(ii) △AGF~△EFC
(iii) △DBG~△EFC
(iv) (DE)2=BD×EC
View Solutionदिए चित्र में , DEFG एक वर्ग है और ∠BAC=90∘ है सिद्ध कीजिये कि :
(i) ΔAGF~ΔDBG
(ii) ΔAGF~ΔEFC
(iii) ΔDBG~ΔEFC
(iv) DE2=BD×EC

View SolutionIn the reaction CH3−CH2−Br+2Na+Br−CH2−CH3dry ether−−−−→ΔA+B
A and B are __________ respectively
View Solutionఏ అవయవాలు కవాటాలు కల్గి ఉంటాయి ?br i) గుండెbr ii) ధమనిbr iii) సిరలుbr iV) శోషరస నాళాలు
View Solutionవేర్ల ద్వారా శాఖీయోత్పత్తి జరిపే మొక్కbr i) డాలియాbr ii) ముల్లంగిbr iii) క్యారెట్br iv) క్యాబేజిbr
View SolutionIf the bond energies of H-H, Br-Br and H-Br are 433, 192 and 364 kJ mol−1 respectively, then ΔH∘ for the reaction :
H2(g)+Br2(g)→2HBr(g) is
View SolutionIn fig.7.84, DEFG is a square and ∠BAC=90°. Prove that:
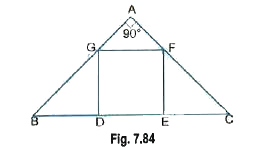
(i) ΔAGF~ΔDBG (ii) ΔAGF~ΔEFC(iii) ΔDBG~ΔEFC (iv) DE2=BD×EC
View SolutionIf the bond energies of H-H, Br-Br and HBr are 433,192and364kJmol−1 respectively, then ΔH∘ for the reaction :
H2(g)+Br2(g)→2HBr(g) is
View SolutionPhytochemistry as a criterion for the classification of organisms is also used by taxonomist in br i. Artificial system, br ii. Cytotaxonomy
View Solution