दिए चित्र में , DEFG एक वर्ग है और ∠BAC=90∘ है सिद्ध कीजिये कि :
(i) ΔAGF~ΔDBG
(ii) ΔAGF~ΔEFC
(iii) ΔDBG~ΔEFC
(iv) DE2=BD×EC

(i) ∴□DEFG एक वर्ग है
∴ GF||BC
⇒ ∠2=∠4 और ∠6=∠9 (संगत कोण)
अब ΔAGF और ΔDBG में
∠5=∠1 (प्रत्येक 90∘)
∠4=∠2 (संगत कोण)
(ii) ΔAGF और ΔEFC में
∠5=∠8 (प्रत्येक 90∘)
∠6=∠9 (संगत कोण)
(iii) ∴ ΔAGF~ΔDBG [ (i) में सिद्ध किया है]
और ΔAGF~ΔEFC [ (ii) में सिद्ध किया है]
∴ ΔAGF~ΔDBG~ΔEFC यही सिद्ध करना था
(iv) अब ∴ DBEF=DGEC (समरूप त्रिभुजों कि संगत भुजाए समानुपाती होती है)
⇒ DG×EF=BD×EC
⇒ DE×DE=BD×EC (∴DG=FE=DE वर्ग की भुजाये)
⇒ DE2=BD×EC यही सिद्ध करना था
यदि हमें केवल चौथा भाग सिद्ध करना है अर्थात DE2=BD×EC सिद्ध करना है तो पहले दो भाग करने में आवश्यकता नहीं है
DE2=BD×EC के लिए हमें ऐसे दो त्रिभुज समरूप सिद्ध करने है जिनमे भुजाये DE,BD और EC है ΔGBD और ΔFEC ऐसे दो त्रिभुज है
अब ΔGBD और ΔFEC में
∠1=∠8 (प्रत्येक 90∘)
∠3=∠9 (अभी सिद्ध किया है)
DG×EF=BD×EC
⇒ DE×DE=BD×EC (∴DG=EF=DE, वर्ग की भुजाये)
⇒ DE2=BD×EC यही सिद्ध करना था
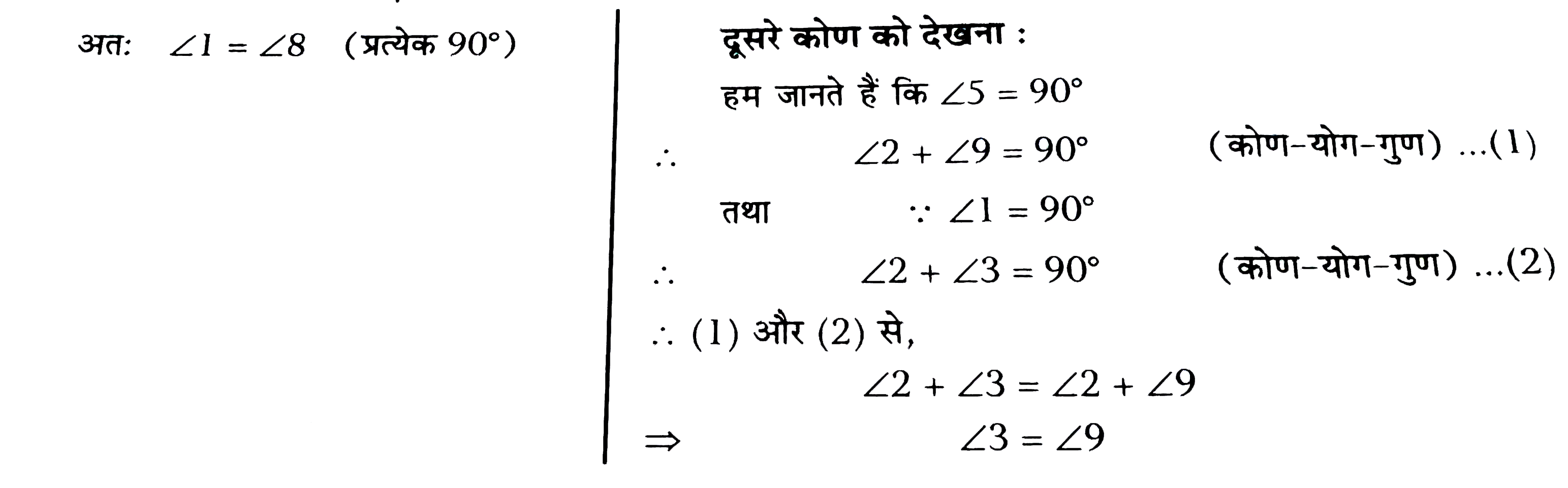

Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6A
24 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6B
26 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)
6 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - NOOTAN HINDICHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
7 Videos
Similar Questions
संलग्न चित्र में , बिन्दु D , AB को 3:5 में विभाजित करता है ज्ञात कीजिये
(i) AEEC (ii) ADAB (iii) AEAC
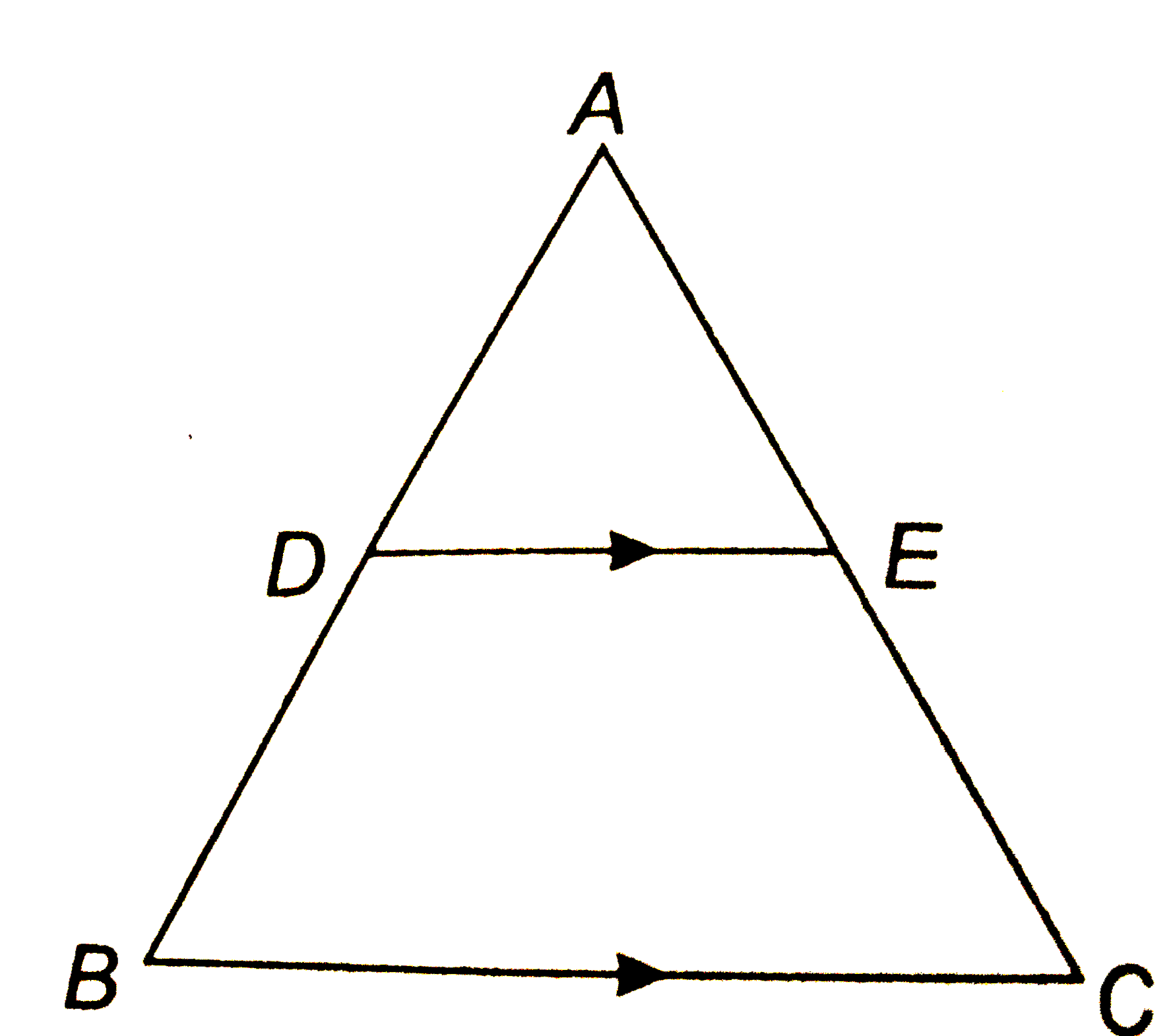
View Solutionदिए चित्र में यदि, AB||CD तो सिद्ध कीजिये कि ΔAOB~ΔDOC
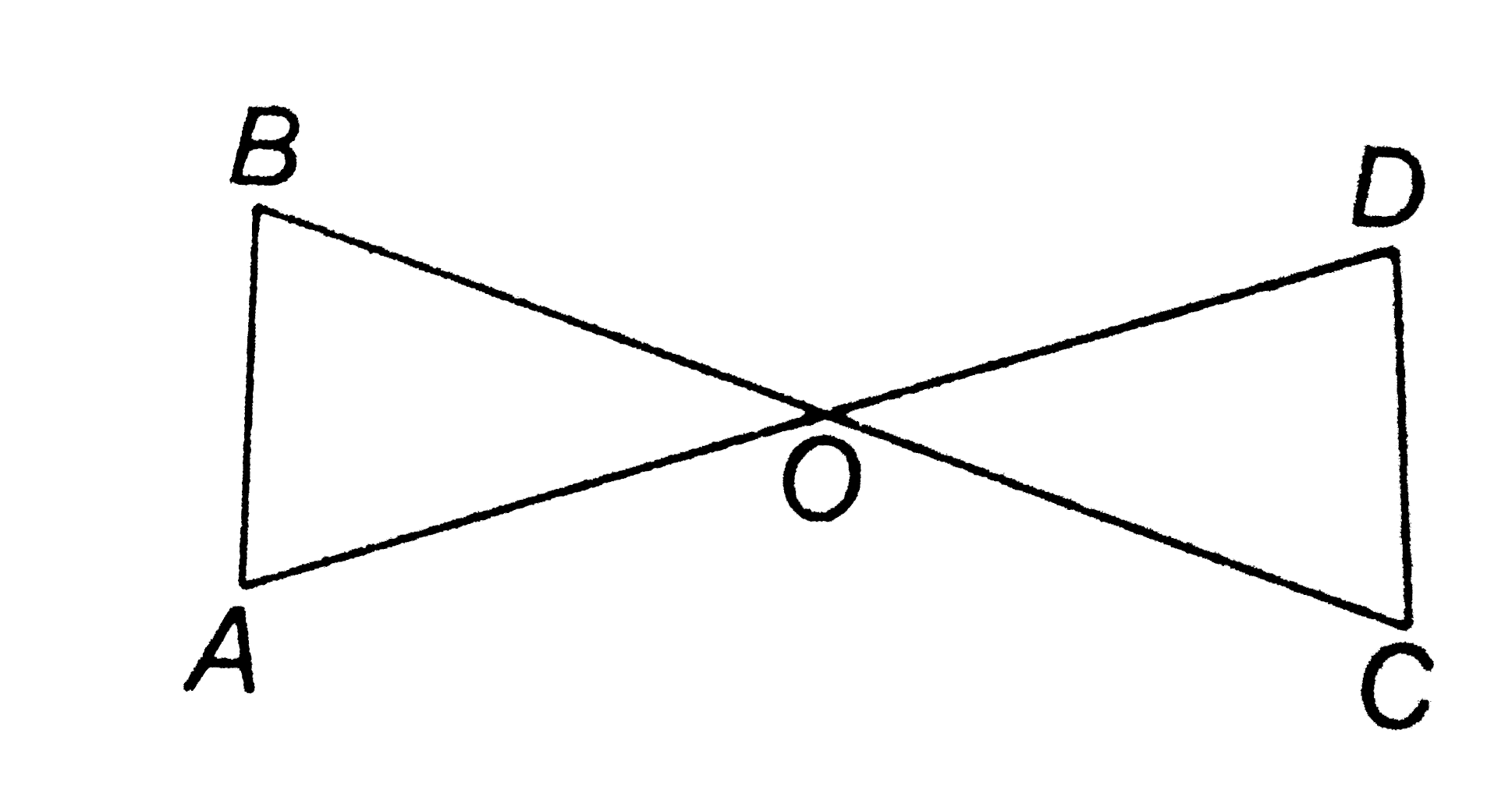
View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
View SolutionWhich of the following symbols are not acceptable ? (i) ._(35)^(79)Br (ii) .^(79)Br (iii) ._(79)^(35)Br (iv) ._(35)Br
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View Solution
