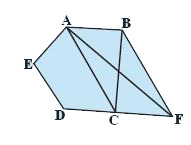
दिए गए आकृति में ABCDE एक पंचभुज है| B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC से F पर मिलती है |दर्शाइए की
(1)ar(ACB)=ar(ACF)
(ii)ar(AEDF)=ar((ABCDE)
(##KCSHINMATIXC11SLV029_Q01##)
(i)Δ(ACB) और ΔACF एक ही आधार AC पर खड़े है तथा दो समांतर रेखाओं AC और BF के बीच स्थित है|
∴ ar(ΔACB)=ar(ΔACF) ltBrgt (ii) ar(AEDF)=ar(AEDC)+ar(ΔACF)
=ar(AEDC)+ar(ΔACB)
=ar(ABCDE)
(##KCSHINMATIXC11SLV029_S01##)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 11.1
24 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
- हीरोन का सूत्र BOOK - KC SINHACHAPTER - हीरोन का सूत्र EXERCISE - वस्तुनिष्ठ प्रश्न
13 Videos
Similar Questions
रिक्त स्थान को भरें :
(i) सर्वांगसम आयतों के क्षेत्रफल ...........होते है|
(ii) किसी समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का .....होता है
(iii) समलम्ब का क्षेत्रफल उसके समांतर भुजाओं के बीच की दुरी तथा समांतर भुजाओं के योग के गुणनफल का ......होता है|
(iv) सर्वांगसम त्रिभुजों के क्षेत्रफल ........होते है|
(v) एक ही आधार तथा एक ही समांतर रेखाओं के मध्य बने त्रिभुज क्षेत्रफल में ...........होते है|
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
View Solutionयदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
View Solutionआकृति में ABCDE एक पंचभुज है । B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है दर्शाइए कि
(i)ar(ACB)=ar(ACF)
(ii)ar=(AEDF)=ar(ABCDF)
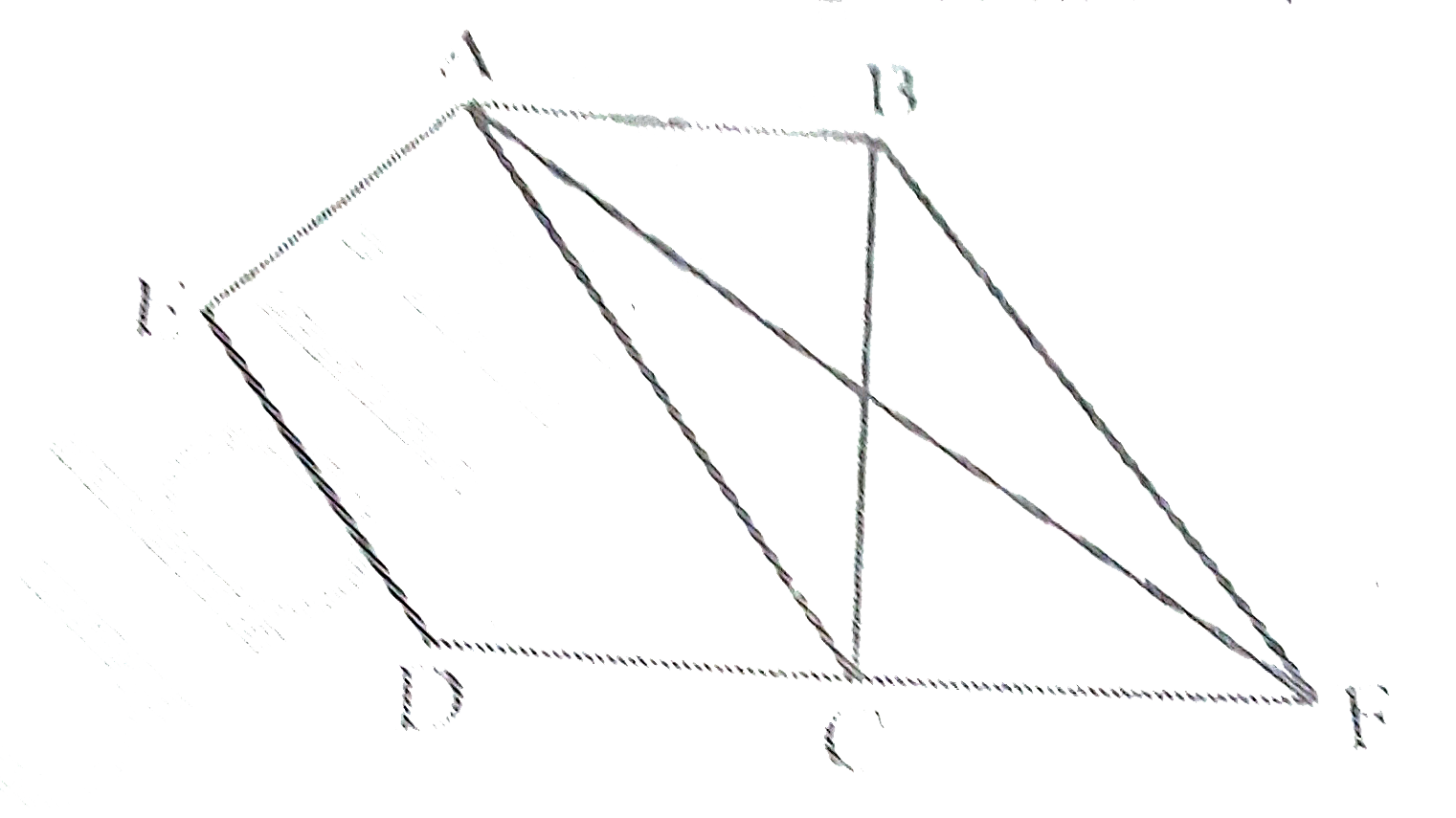
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही AL⊥DC, तो सिद्ध कीजिए कि
(i)ar(ABCD)=ar(EFCD)
(ii)ar(ABCD)=DC×AL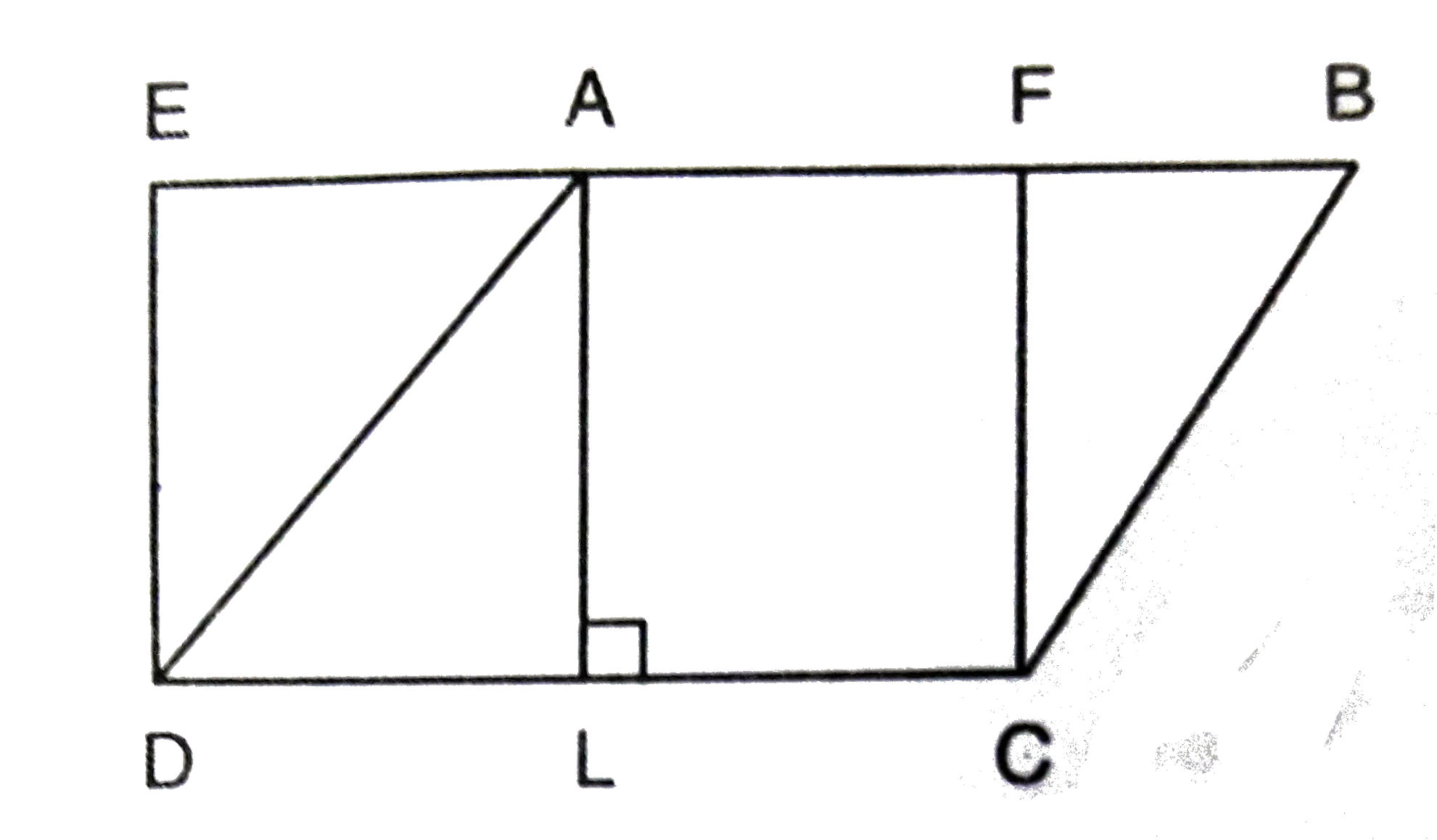
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionIn, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i)ar (ACB) = ar (ACF)
(ii)ar (AEDF) = ar(ABCDE)
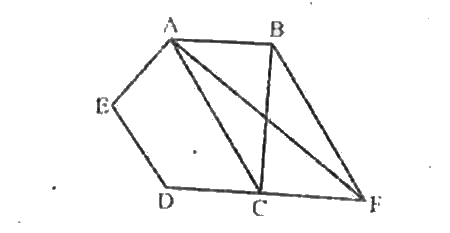
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View SolutionFactorise:
ar+br+at+bt
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB)=ar(ΔACF)
(ii) ar(AEDF)=ar(ABCDE)
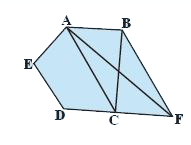
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that (i) ar (DeltaACB) = ar (DeltaACF) (ii) ar (AEDF) = ar (ABCDE)
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB)=ar(ΔACF)
(ii) ar(AEDF)=ar(ABCDE)
View Solution
