समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित है कि DP=BQ है । दर्शाइए कि
(i) ΔAPD≅CQB (ii) AP=CQ
(iii) ΔAQB≅ΔCPD (iv) AQ=CP
(v) APCQ एक समांतर चतुर्भुज है।
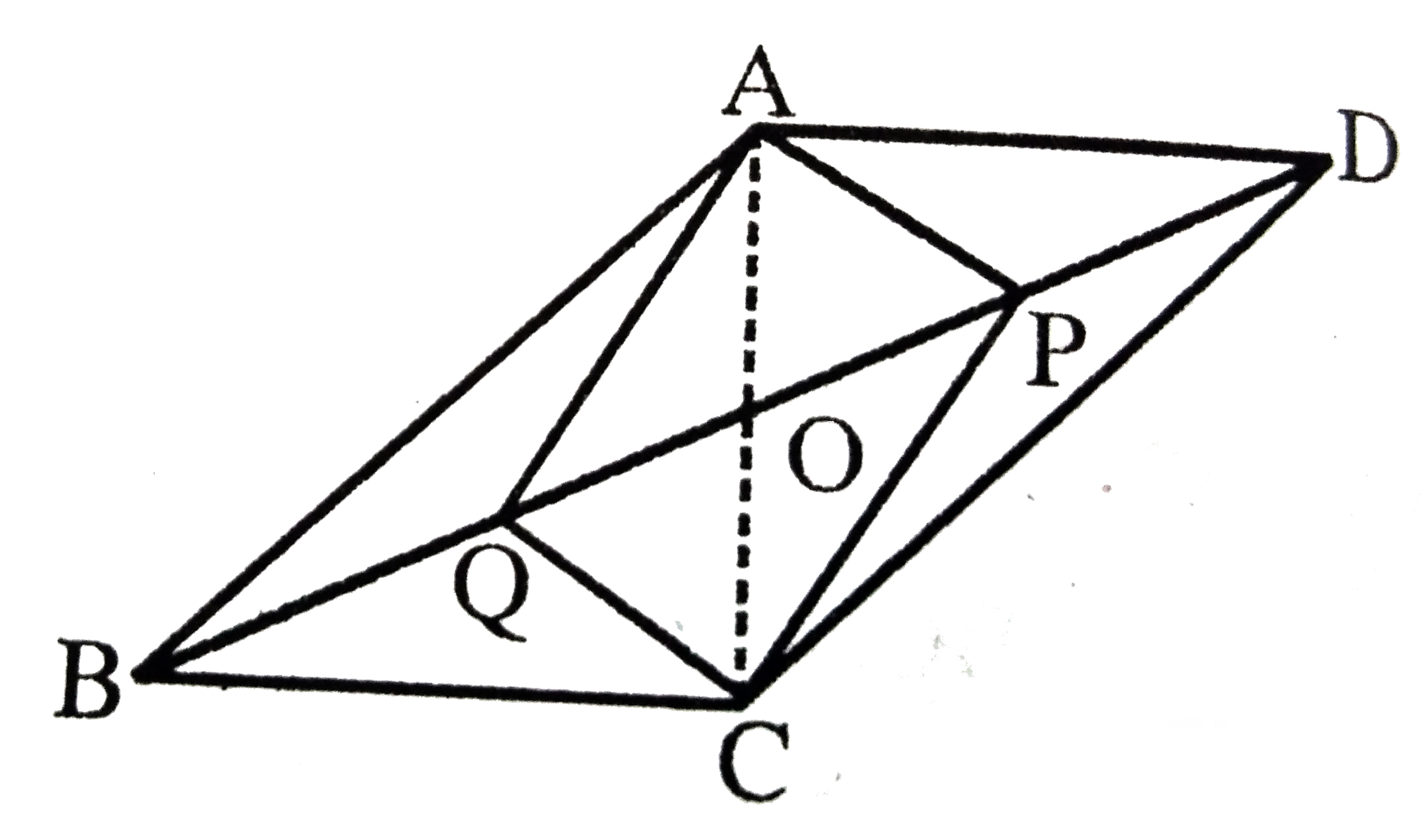
AC को मिलायें जो BD को O बिंदु पर काटता है।
अब OP=OD−DP
तथा OQ=OB−BQ
लेकिन OB=OD
[ ∵ समांतर चतुर्भुज के कर्ण एक-दूसरे को समद्विभाजित करते हैं।]
तथा DP=BQ [दिया हुआ है]
∴OP=OQ
अतः चतुर्भुज APCQ से OP=OQ तथा OA=OC
अर्थात चतुर्भुज APCQ के कर्ण एक-दूसरे को समद्विभाजित करते हैं।
∴ चतुर्भुज APCQ एक समांतर चतुर्भुज है।
अब ΔAPD तथा ΔCQB में AD=BC
AP=QC [∵APCQ एक समांतर चतुर्भुज है]
DP=BQ [दिया है]
∴ΔAPD≅ΔCQB [SSS सर्वांगसमता नियम से]
ΔAQB तथा ΔCPD में AB=DC
AQ=PC [∵APCQ एक समांतर चतुर्भुज है]
BQ=DP [दिया है]
∴ΔAQB≅ΔCPD [SSS सर्वांगसमता से]
Topper's Solved these Questions
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - अतिलघु उत्तरीय प्रश्न (समांतर चमुर्भुज, आयत, वर्ग तथा समचतुर्भुज से संबंधित परिभाषाओं, प्रमेयों तथा उपप्रमेयों के सीधे प्रयोग पर आधारित प्रश्नः)
16 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - लघु उत्तरीय प्रश्न
4 Videos
- वृत्त BOOK - KC SINHACHAPTER - वृत्त EXERCISE - वस्तुनिष्ठ प्रश्न
17 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
Similar Questions
रिक्त स्थानों को भरें:
कोई समांतर चतुर्भुज एक समचतुर्भुज होगा यदि और केवल यदि उसके...................... एक-दूसरे पर लम्ब हो।
View Solutionकिसी समांतर चतुर्भुज ABCD में ∠D=110∘ तो ∠A एवं ∠B की माप अंशों में लिखें।
View Solutionवृत्त पर किन्ही दो बिन्दुओं को मिलाने वाली रेखाखंड को क्या कहते है ?
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
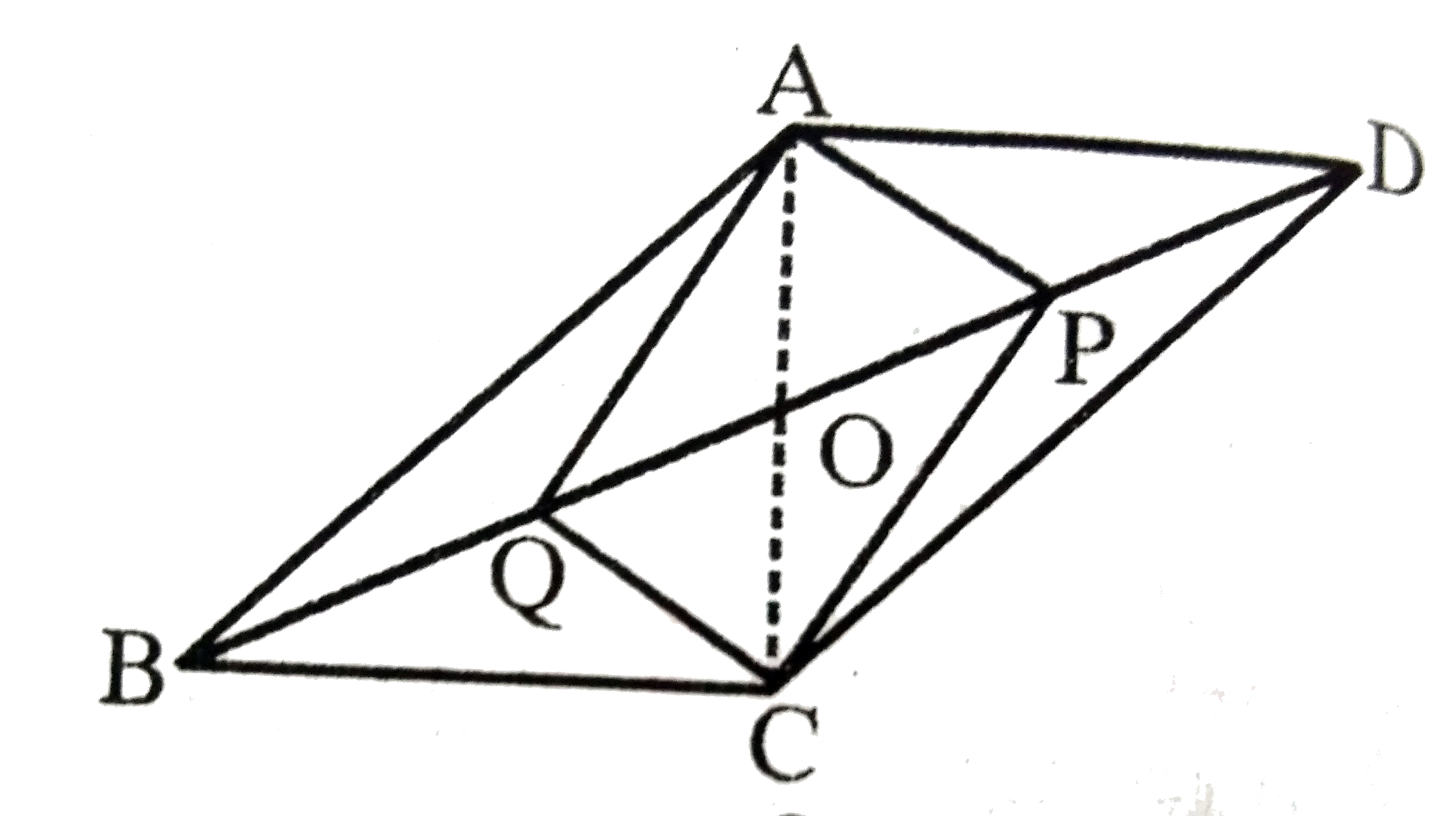
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionसमांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित है कि DP=BQ है। दर्शाइए कि
(i) ΔAPD≅ΔCQB
(ii)AP=CQ
(iii) ΔAQB≅ΔCPD
(iv)AQ=CP
( v) APCQ एक समांतर है ।
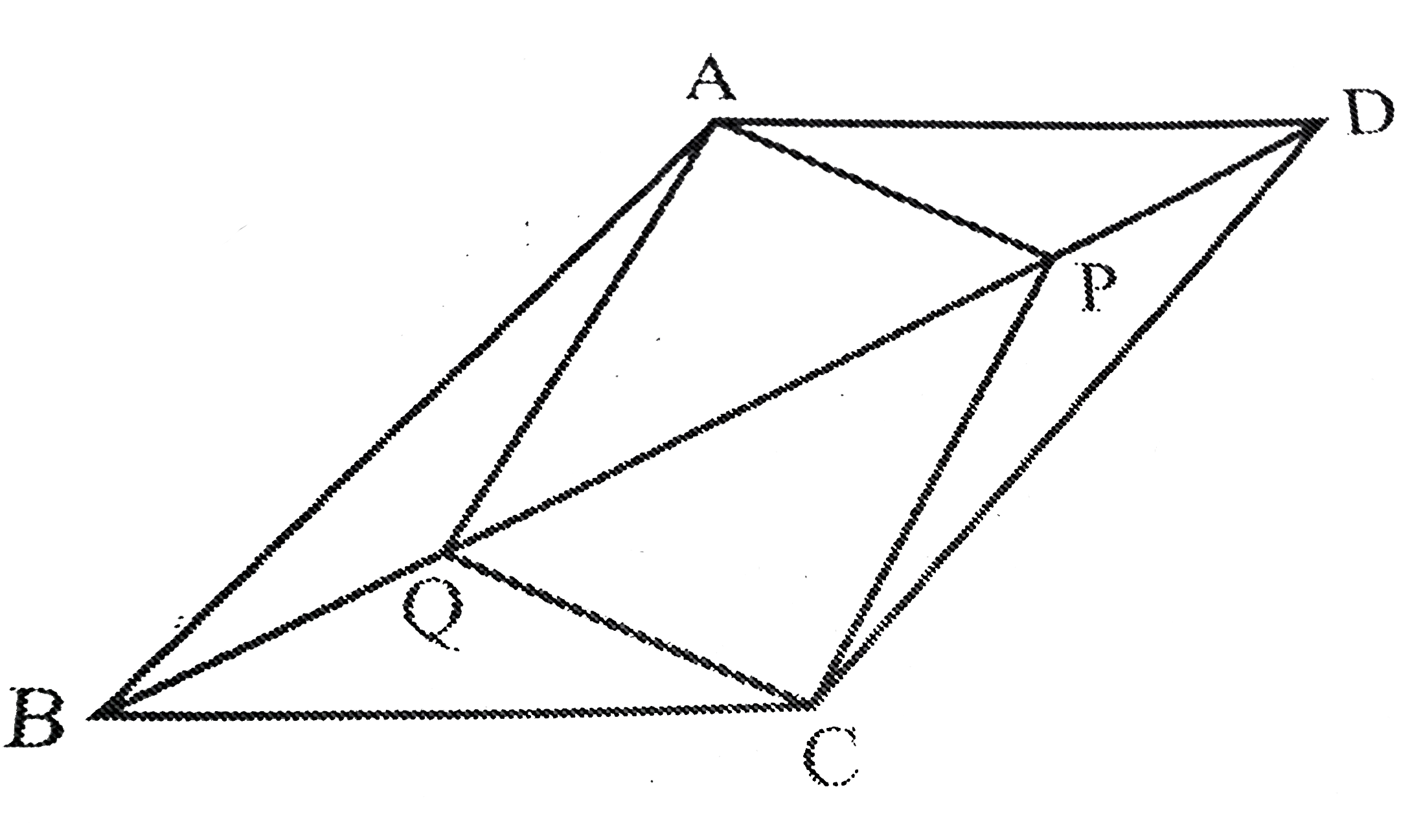
View Solutionसमांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP=BQ है। दर्शाइए कि:
(i) ΔAPD≅ΔCQB (ii) AP=CQ
(iii) ΔAQB≅ΔCPD (iv) AQ=CP
(v) APCQ एक समांतर चतुर्भुज है।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View Solution
