समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP=BQ है। दर्शाइए कि:
(i) ΔAPD≅ΔCQB (ii) AP=CQ
(iii) ΔAQB≅ΔCPD (iv) AQ=CP
(v) APCQ एक समांतर चतुर्भुज है।
दिया है ABCD एक समांतर चतुर्भुज है और P और Q,BD पर इस प्रकार स्थित हैं कि

DP=BQ……………1
(i) हम सिद्ध करेंगें कि
ΔAPD≅ΔCQB
अब ΔAPD और ΔCQB में
∵⎧⎪
⎪⎨⎪
⎪⎩DP=BQ(दिया है)AD=BC(समांतर चतुर्भुज की सम्मुख भुजाएं)∠1=∠2(एकांतर कोण)
∴ΔAPD≅ΔCQB (S.A.S. से)
(ii) ∵ΔAPD≅ΔCQB (सिद्ध कर चुके हैं।)
∵AP=CQ
(iii) यहां हम सिद्ध करेंगे कि ΔAQB≅ΔACPD
अब ΔAQB और ΔCPD में
∵⎧⎪
⎪⎨⎪
⎪⎩BQ=DE(दिया है)AB=CD(समांतर चतुर्भुज की सम्मुख भुजाएं)∠3=∠4(एकान्तरकोण)
∴ΔAQB≅ΔCPD (S.A.S)
(iv) ∵ΔAQB=ΔCPD
∴AQ=CP
(v) ∵AP=CQ [भाग ii से]
और AQ=CP [भाग iv से]
∴□APCQ एक समांतर चतुर्भुज है।
( ∵सम्मुख भुजाओं के युग्म बराबर है)
Topper's Solved these Questions
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:प्रश्नावली 8.2
Explore 7 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:प्रश्नावली 8B
Explore 15 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:दीर्घ उत्तरीय प्रश्न
Explore 5 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
Explore 8 Videos
Similar Questions
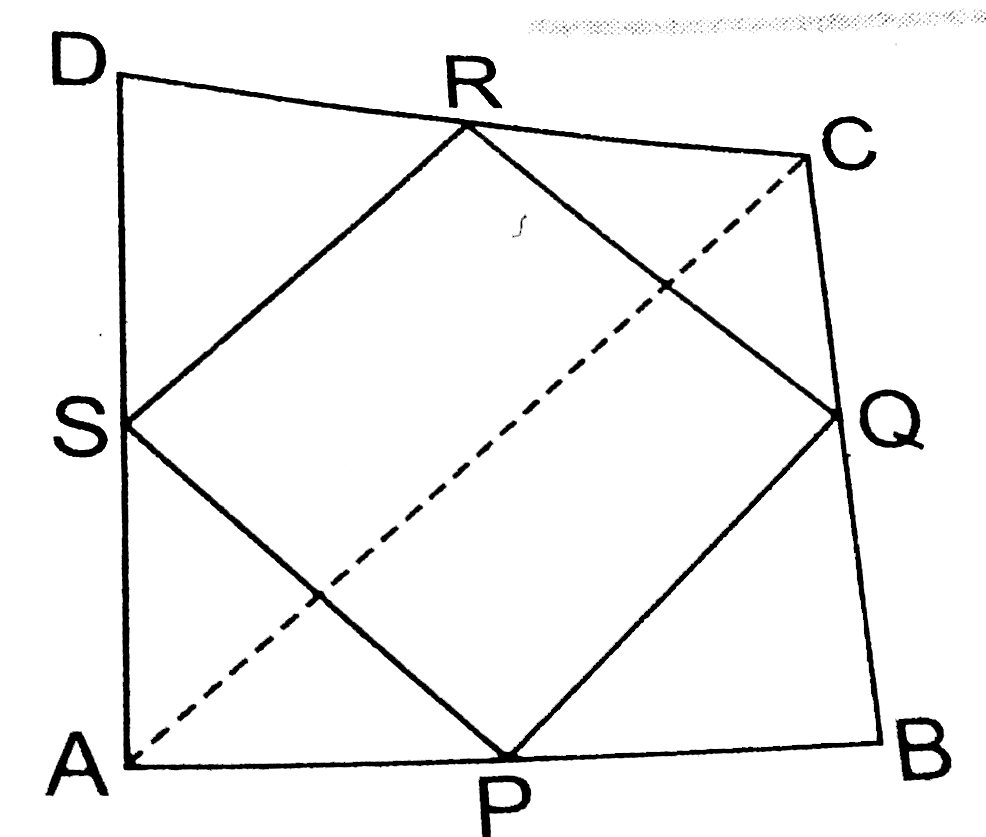
ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु हैं । AC उसका एक विकर्ण है। दर्शाइए कि:
(i) SR∣∣AC और SR=12AC है।
(ii) PQ=SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।
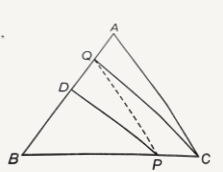
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
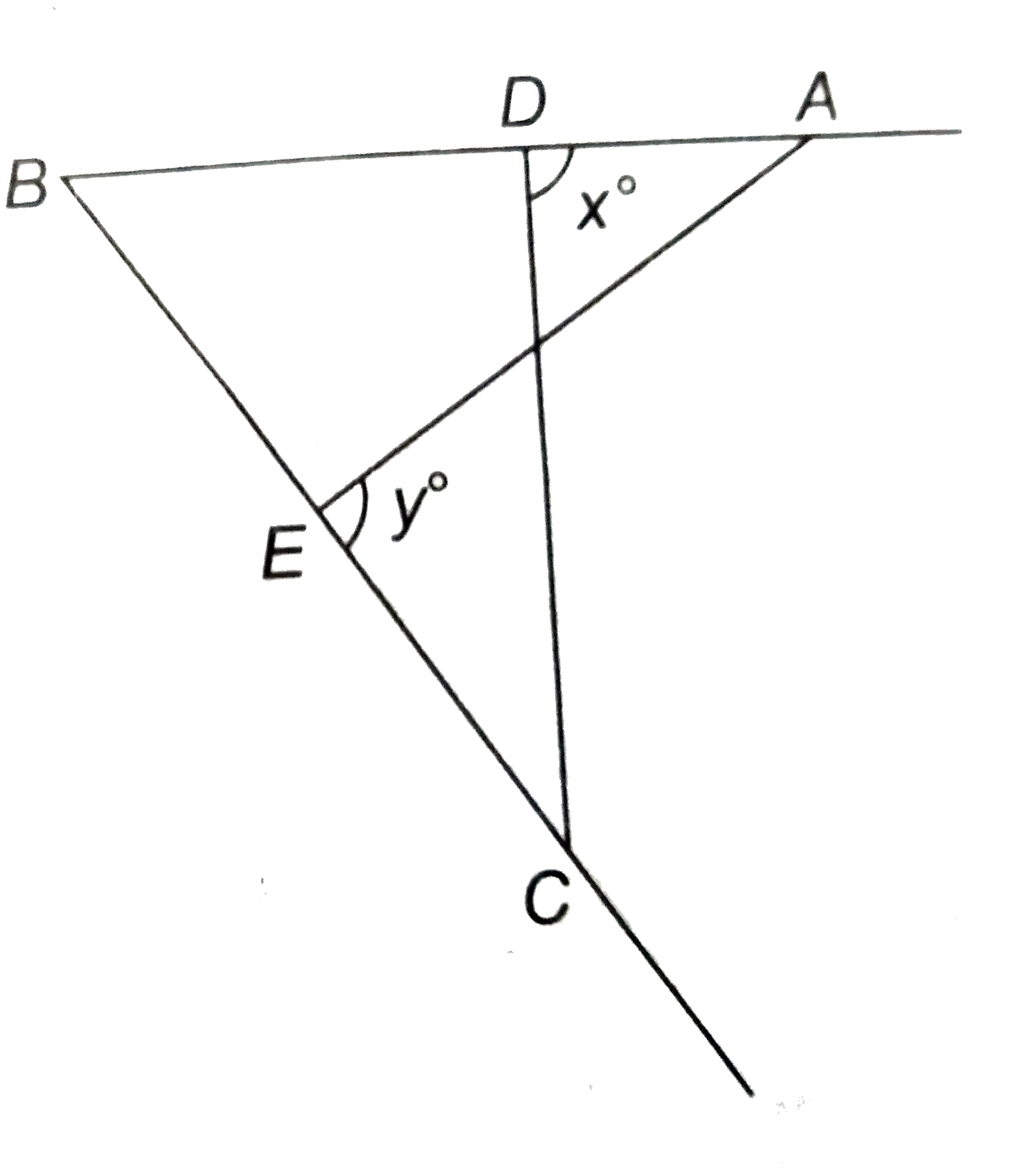
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt
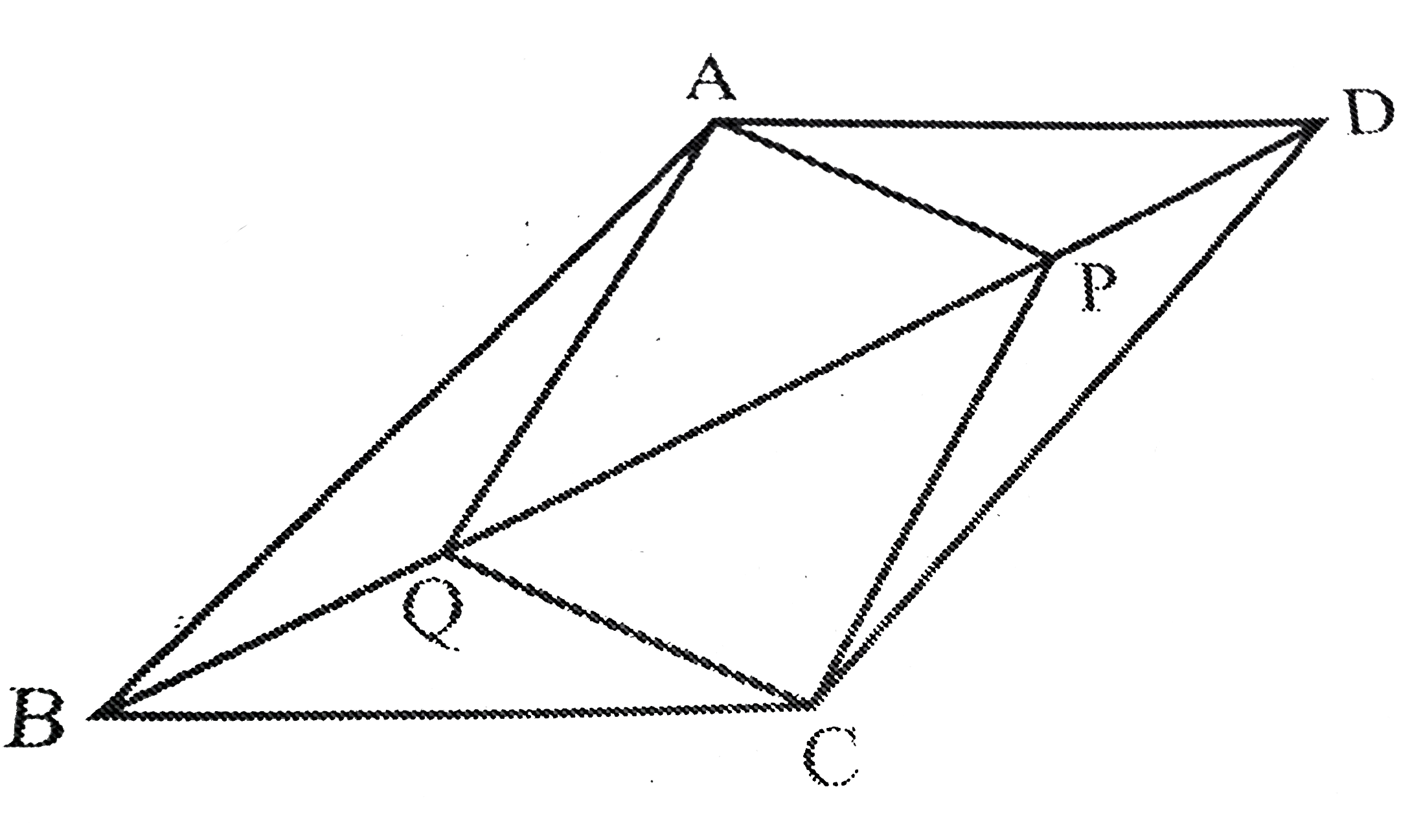
View Solutionसमांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित है कि DP=BQ है। दर्शाइए कि
(i) ΔAPD≅ΔCQB
(ii)AP=CQ
(iii) ΔAQB≅ΔCPD
(iv)AQ=CP
( v) APCQ एक समांतर है ।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionसिध्द कीजिए कि सम्मिश्र संख्याओं 6−i,7+3i,8+2i और 7 - 2i को निर्मित करने वाले बिंदु एक समांतर चतुर्भुज बनाते हैं ।
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP=BQ show that
ΔAPD≈ΔCQB
ΔAQB≈ΔCPD
AQ=CP
APCQ is a parallelogram
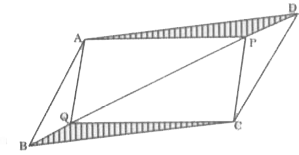
View SolutionP and Q have taken two points on the diagonal BD to be DP = BQ in the ABCD parallelogram (see Figure) (i) triangleAPD cong triangleCQB (ii) AP = CQ (iii) triangleAQB cong triangleCPD (iv) Show that AQ = CP (v) APCQ is a parallelogram.
View Solutionसमांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु Pऔर Q इस प्रकार स्थित हैं कि DP = BQ हैं ( देखिए आकृति)।दर्शाइए कि-
ΔAPDE≅ΔCQB
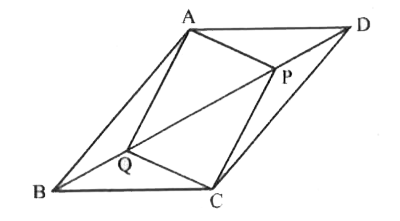
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt
View SolutionThe length of two sides of a parallelogram are 3cm and 10 cm. What is the sum of the squares of diagonals of the parallelogram ? एक समांतर चतुर्भुज के दो भुजाओं की लंबाई 3 सेमी और 10 सेमी है। समांतर चतुर्भुज के विकर्णों के वर्गों का योग क्या होगा ?
View Solutionचतुर्भुज |चतुर्भुज का कोण योग गुण |चतुर्भुज के प्रकार |समांतर चतुर्भुज के गुण|प्रमेय|सारांश
View Solution

