Question

Radius of gyration of a body about an axis at a distance 6 cm from its centre of mass is 10 cm. Find its radius of gyration about a parallel axis through its centre of mass.

Options

A. 800 cm
B. 8 cm
C. 0.8 cm
D. 80 m

Answer

B

Explanation

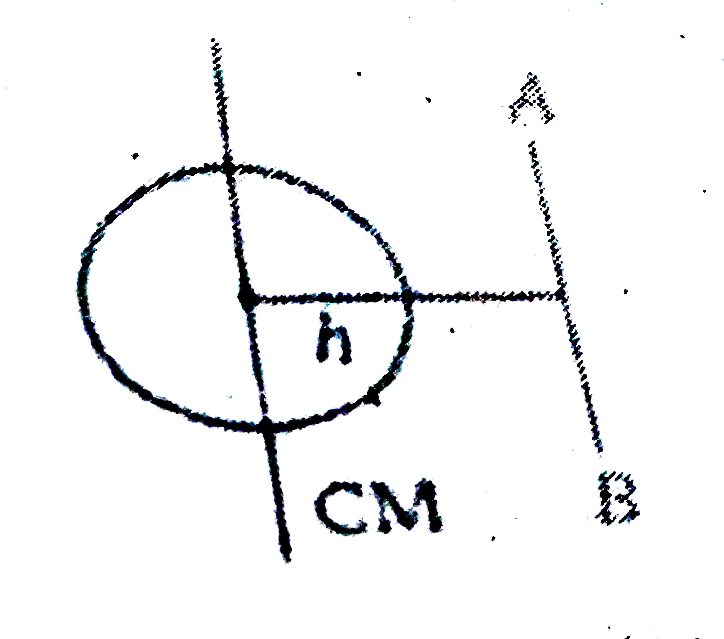
`T_(AB)=I_(CM)+Mh^(2)`
`MK_(AB)^(2)=MK_(CM)^(2)+Mh^(2)`
`K_(AB)^(2)=K_(CM)^(2)+h^(2)`
given, `K_(AB)=10cm,h=6cm`
Putting them, we get
`K_(CM)=8cm`