Radius of gyration of a ring about a transverse axis passing through its centre is
0.5× diameter of ring
diameter of ring
2× diameter of ring
(diameter of ring)2
The correct Answer is:A
To find the radius of gyration of a ring about a transverse axis passing through its center, we can follow these steps:
1. Understanding the Problem: We need to find the radius of gyration (k) of a ring when it rotates about a transverse axis that passes through its center.
2. Define the Ring: Let's denote the mass of the ring as m and the radius of the ring as r.
3. Moment of Inertia: The moment of inertia I of a ring about an axis passing through its center and perpendicular to its plane (transverse axis) is given by the formula:
I=mr2
4. Radius of Gyration: The radius of gyration k is related to the moment of inertia by the equation:
I=mk2
5. Equating the Two Expressions: Since we have two expressions for the moment of inertia, we can set them equal to each other:
mr2=mk2
6. Simplifying the Equation: We can cancel m from both sides (assuming m≠0):
r2=k2
7. Finding the Radius of Gyration: Taking the square root of both sides gives us:
k=r
8. Interpreting the Result: The radius of gyration of the ring about the transverse axis passing through its center is equal to the radius of the ring.
9. Answering the Question: If the question asks for the radius of gyration in terms of the diameter of the ring, we can express it as:
k=12×diameter of the ring
Final Answer:
The radius of gyration of a ring about a transverse axis passing through its center is 12 times the diameter of the ring.
---
I=mr2
I=mk2
mr2=mk2
r2=k2
k=r
k=12×diameter of the ring
The radius of gyration of a ring about a transverse axis passing through its center is 12 times the diameter of the ring.
Topper's Solved these Questions
Similar Questions
There is a uniform circular disc of mass 10kg & radius 2 meter. Calculate the radius of gyration if it is rotating about an axis passing through its centre & perpendicular to its plane
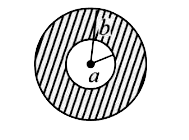
View SolutionA circular disc of radius b has a hole of radius a at its centre (see figure). If the mass per unit area of the disc varies as (σ0r). then the radius of gyration of the disc about its axis passing through the centre is:
View Solution
Knowledge Check
If the moment of inertia of a ring about transverse axis passing through its centre is 6 kg m2, then the M.I. about a tangent in its plane will be
A3kgm2B9kgm2C6kgm2D12kgm2Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
AR/√2BR/2C√2 RD2RRadius of gyration of a body about an axis is 12 cm. Radius of gyration of the same body about a parallel axis passing through its centre of gravity is 13 cm. T?hen perpendicular distance between the two axes is
A5 cmB1 cmC15 cmD10 cm
Radius of gyration of a body an axis is 1 cm. Radius of gyration of the same body about a parallel axis passing through its centre of gravity is 2 cm. then perpendicular distance between the two axes is
View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is K, If radius of the ball be R, then the fraction of total energy associated with its rotational energy will be
View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
View SolutionA body rolls without slipping. The radius of gyration of the body about an axis passing through its centre of mass is K. The radius of the body is R. The ratio of rotational kinetic energy to translational kinetic energy is.
View SolutionA ball rolls without slipping. The radius of gyration of the ball about about an axis passing through its center of mass is K. If radius of the ball be R, then the fraction of total energy associated with its rotational energy be
View Solution
