The variation of volume V, with temperature T, keeping pressure constant is called the coefficient of thermal expansion (α) of oa gas, i.e., α=1V=(δVδT)P.
For an ideal gas α is equal to
T
1/T
P
1/P
The correct Answer is:B
For n moles of an ideal gas PV = nRT
or V=RTP
Differentiating with respect to T at constant P, we have
(∂V∂T)P=nRp=VT
α=1V=(∂V∂T)P=1V×VT=1T
Topper's Solved these Questions
Similar Questions
Knowledge Check
An ideal gas has a volume of 3V at 2 atmosphere pressure. Keeping the temperature constant. Its pressure is doubled. The volume of the gas will be
A6VB3VC1.5VD1VFor an ideal gas PT11 = constant then volume expansion coefficient is equal to :-
A11TB1TC12TD2TWhich of the following graphs correctly represents the variation of β=−dV/dPV
with P for an ideal gas at constant temperature?A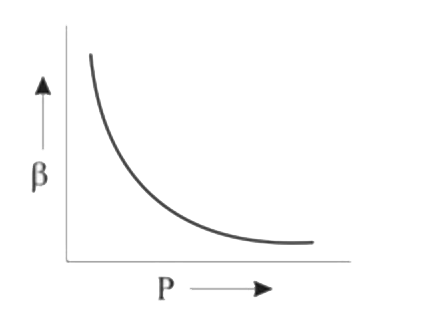 B
B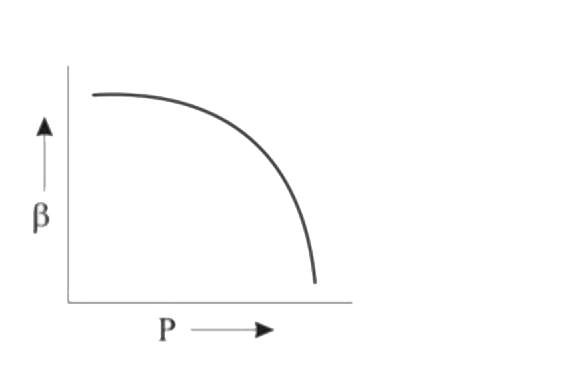 C
C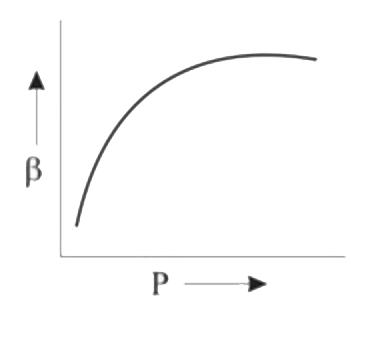 D
D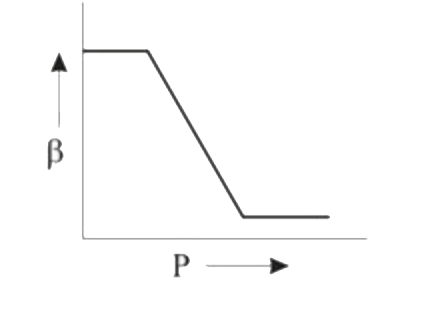
Show that the volume thermal expansion coefficient for an ideal gas at constant pressure is 1T.
View SolutionAn ideal gas has pressure P, volume V and temperature T. Select the correct option.
View SolutionCalculate the isothermal compressibility 'alpha' for an ideal gas [α=−1V(δVδV)T.n]atP=1 bar and cubic
expansion coefficient β[β=−1V(δPδT)P.n]for an ideal
gas at T=273K .
View SolutionA glass vessel of volume v0 is completely filled with a liquid and its temperature is raised by ΔT. What volume of the liquid will overflow? Coefficient of linear expansion of glass =α−(g) and coefficient of volume expansion of the liquid =γc
View SolutionThe average speed of gas molecules is v at pressure P, If by keeping temperature constant the pressure of gas is doubled, then average speed will become
View Solution

