How many geometrical isomers are possible in the following two alkenes?
(i)
4 and 4
4 and 3
3 and 3
3 and 4
The correct Answer is:D
To determine the number of geometrical isomers for the given alkenes, we will analyze each compound step by step.
Step 1: Analyze the first alkene CH₃−CH=CH−CH=CH−CH₃
1. Identify the double bonds: The first alkene has two double bonds (C=C).
2. Identify sp² hybridized carbons: Each carbon involved in a double bond is sp² hybridized. Here, we have 4 sp² hybridized carbons.
3. Check for identical end groups: The end groups of this alkene are both methyl groups (CH₃), which are identical.
Formula for geometrical isomers: When the end groups are similar, the formula to find the number of geometrical isomers is:
\( \text{Number of isomers} = 2^n \)
where \( n \) is the number of double bonds.
- Here, \( n = 2 \) (two double bonds).
- Thus, the number of geometrical isomers is:
\( 2^2 = 4 \)
Step 2: Analyze the second alkene CH₃−CH=CH−CH=CH−Cl
1. Identify the double bonds: The second alkene also has two double bonds (C=C).
2. Identify sp² hybridized carbons: Again, we have 4 sp² hybridized carbons.
3. Check for identical end groups: The end groups of this alkene are CH₃ (methyl) and Cl (chlorine), which are different.
Formula for geometrical isomers: When the end groups are different, the formula to find the number of geometrical isomers is:
\( \text{Number of isomers} = 2^{p-1} + 2^{n-1} \)
where \( p \) is the number of pairs of double bonds and \( n \) is the total number of double bonds.
- Since there are 2 double bonds (even), we calculate \( p \) as:
\( p = \frac{n}{2} = \frac{2}{2} = 1 \)
- Now, substituting \( p \) and \( n \) into the formula:
\( \text{Number of isomers} = 2^{1-1} + 2^{2-1} = 2^0 + 2^1 = 1 + 2 = 3 \)
Summary of Results:
- For the first alkene CH₃−CH=CH−CH=CH−CH₃: 4 geometrical isomers
- For the second alkene CH₃−CH=CH−CH=CH−Cl: 3 geometrical isomers
Final Answer:
- 4 geometrical isomers for the first alkene
- 3 geometrical isomers for the second alkene
---
2. Identify sp² hybridized carbons: Each carbon involved in a double bond is sp² hybridized. Here, we have 4 sp² hybridized carbons.
3. Check for identical end groups: The end groups of this alkene are both methyl groups (CH₃), which are identical.
\( \text{Number of isomers} = 2^n \)
where \( n \) is the number of double bonds.
- Thus, the number of geometrical isomers is:
\( 2^2 = 4 \)
2. Identify sp² hybridized carbons: Again, we have 4 sp² hybridized carbons.
3. Check for identical end groups: The end groups of this alkene are CH₃ (methyl) and Cl (chlorine), which are different.
\( \text{Number of isomers} = 2^{p-1} + 2^{n-1} \)
where \( p \) is the number of pairs of double bonds and \( n \) is the total number of double bonds.
\( p = \frac{n}{2} = \frac{2}{2} = 1 \)
- Now, substituting \( p \) and \( n \) into the formula:
\( \text{Number of isomers} = 2^{1-1} + 2^{2-1} = 2^0 + 2^1 = 1 + 2 = 3 \)
- For the first alkene CH₃−CH=CH−CH=CH−CH₃: 4 geometrical isomers
- For the second alkene CH₃−CH=CH−CH=CH−Cl: 3 geometrical isomers
- 4 geometrical isomers for the first alkene
- 3 geometrical isomers for the second alkene
Topper's Solved these Questions
Similar Questions
Calculate the number of geometrical isomers in the following polyenes.
(i) H3C−CH=CH−CH=CH−CH=CH−CH=CH−Br
(ii) H3C−CH=CH−CH=CH−CH=CH−CH=CH−CH3
(iii) C6H5−CH=CH−CH=CH−CH=CH−C6H5
(iv) C6H5−CH=CH−CH=CH−Cl
View SolutionCompare the stabilites of the following alkenes
CH3−O−CH=CH2
CH3−CH=CH−CH3
View Solution
Knowledge Check
How many geometrical isomers are possible in the following two alkenes ?
(i)CH3−CH=CH−CH=CH−CH3
(ii)CH3−CH=CH−CH=CH−ClA4 and 4B4 and 3C3 and 3D3 and 4How many geometrical isomers are possible for the given compound?
CH3−CH=CH−CH=CH−C2H5AFourBThreeCTwoDFiveHow much geometrical isomers are possible for the given compound?
CH3−CH=CH−CH=CH−CH=CH2A2B3C4D8
How many sigma and pi bonds are present in the following molecules :
(i)CH3−CH3 (ii)CH3−OH (iii)CH2=CH−C≡N (iv)CH2=C=CH2CH3 (v)CH≡CCH=CHCH3
View SolutionHow many geometrical isomers are possible for the given compound?
CH3−CH=CH−CH=CH−C2H5
View SolutionThe number of geometrical isomers in the following compound CH3−CH−CH−CH=CH−C2H5 is:
View SolutionHow many geometrical isomers are possible for the given compound?
Ph-CH=CH-CH=CH-COOH
View SolutionRates of hydration of the following alkene are:
CH3−OCH=CH2 F−CH=CH=CH2 CH3CH=CH2
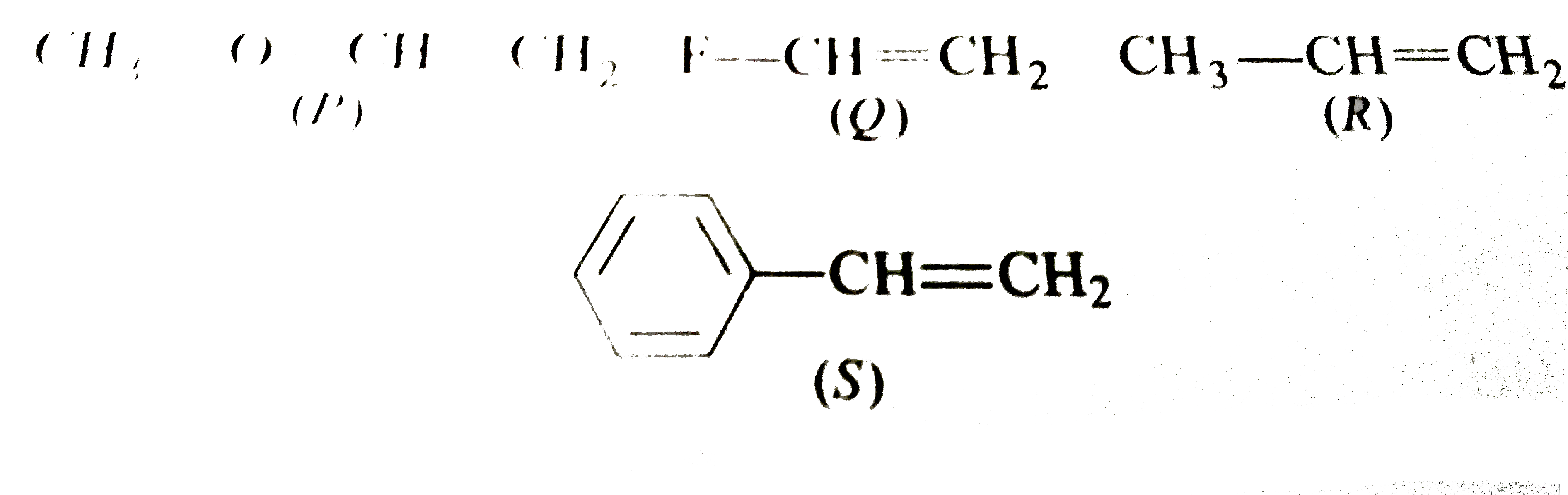
View Solution

