From the given figure find the frequency of oscillation of the mass m

A
n=12π√Km
B
n=12π√K22m
C
n=2π√m2K
D
n=12n√K2m
Video Solution
Text Solution
The correct Answer is:A

If we pull mass m towards right by a distance x then the restoring force it experiences is
F=-kx
⇒md2xdt2=−kx
⇒d2xdt2+kmx=0⇒d2xdt2+ω2x=0
where ω=√xm
⇒2πT=√xm
⇒n=12π√xm

|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkIn figure S1 andS1 are identical springs. The oscillation frequency of the mass m is f. if one spring is removed, the frequency will become
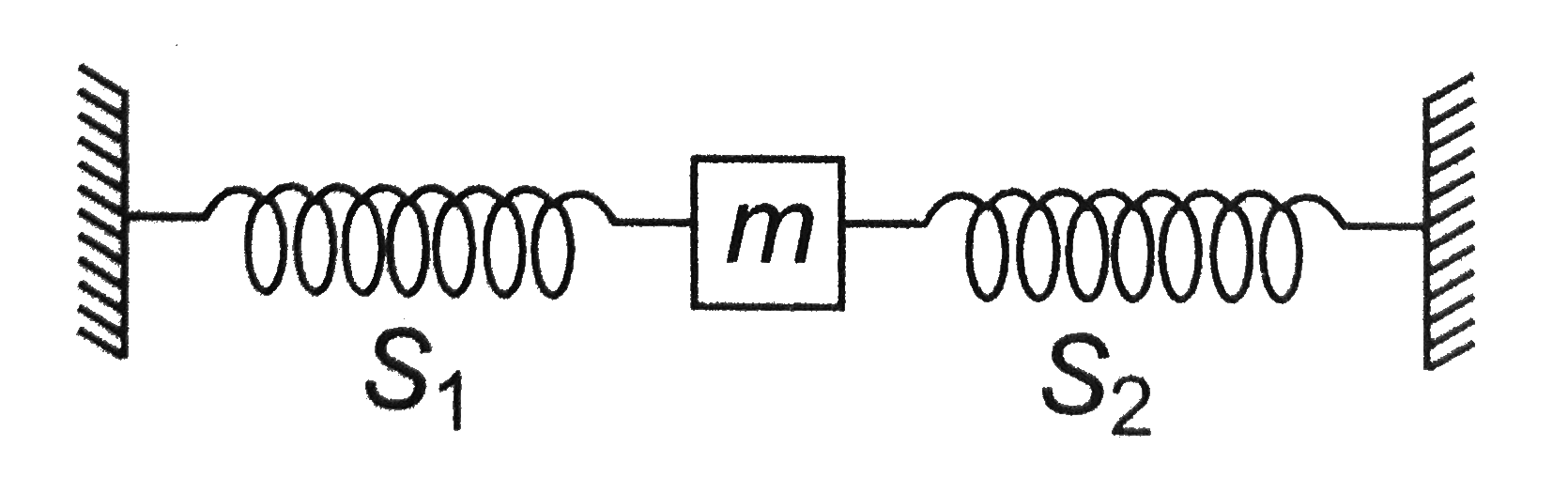 AfB2fC√2fDf√2
AfB2fC√2fDf√2
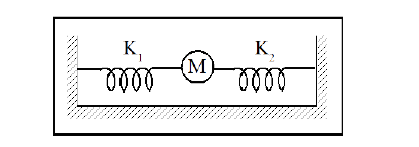
Two spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

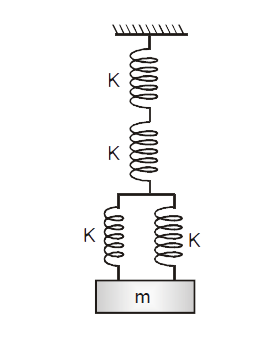
View SolutionThe frequency of oscillation of the system shown in the figure will be
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionThe frequency of LC oscillation is given by
View SolutionThe frequency of oscillation of the springs shown in the figure will be

View Solution