Two masses are attached to a rod end to end . If torque is applied they rotate with angular acceleration α. If their distances are doubled and same torque is applied, then they move with angular acceleration.
4α
α
3α
α/4
The correct Answer is:D
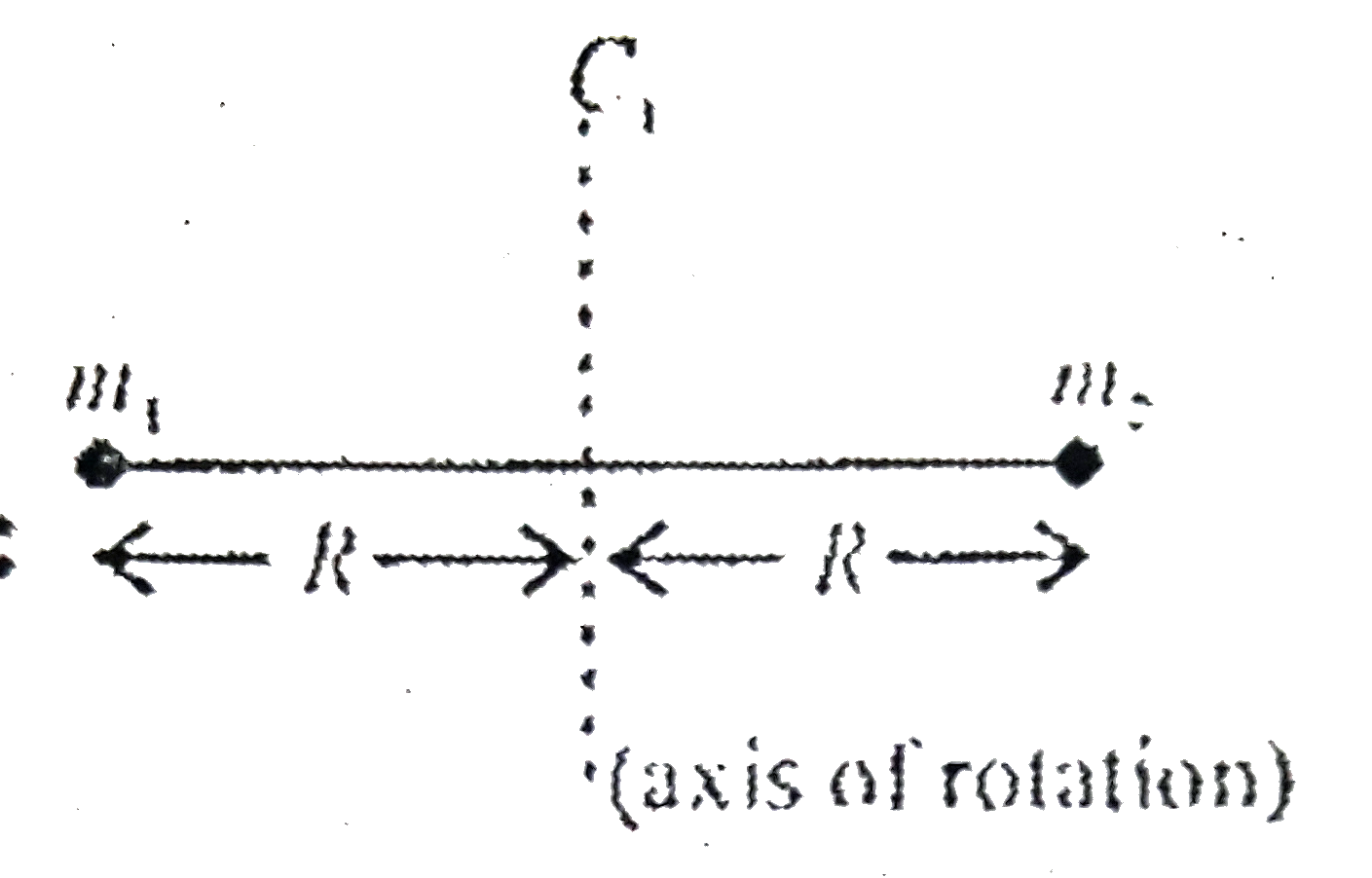
Suppose the masses m1 and m2 are attached to the ends of a massless rod. C1 is the axis of rotation which is at a distance R from each of the masses.
∴ the moment of inertia of the system,
I=m1R2+m2R2=(m1+m2)2R2
Now if the distance between the masses is doubled , then the moment of inertia.
I'=m1(2R)2+m2(2R)2=(m1+m2)4R2
Since the same torque is applied in both the cases,
τ=Iα=IαI'=(m2+m2R2α(m1+m24R2)=α4
Topper's Solved these Questions
Similar Questions
Obtain an expressing for torque acting on a body rotating with uniform angular acceleration.
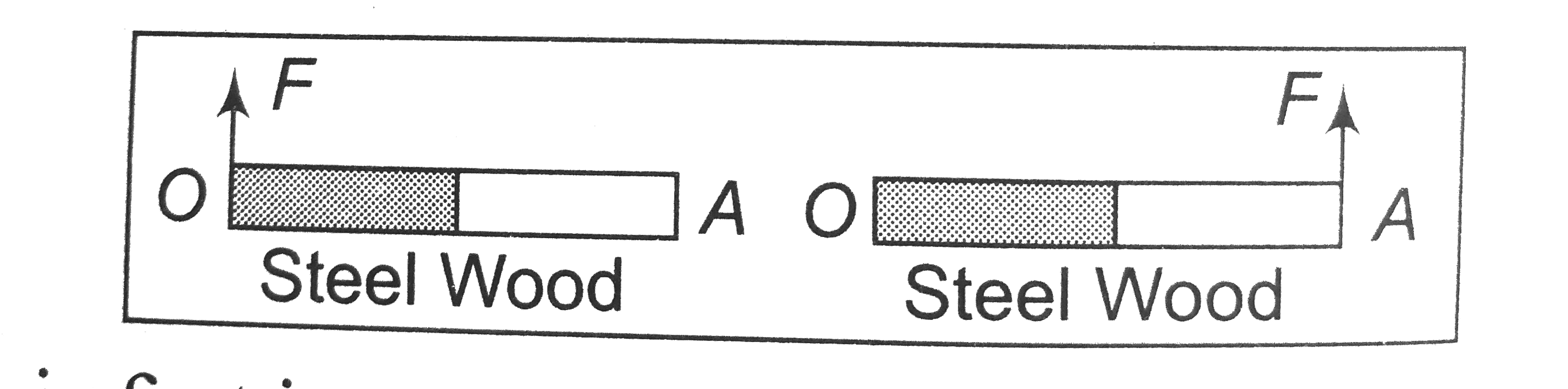
View SolutionIn first figure a meter stick, half of which is wood and the other half steel is pivoted at the wooden end at A and a force is applied at the steel and at O. On second figure the stick is pivoted at the steel end at O and the same force is applied at the wooden end at A. The angular acceleration.
 .
.
View Solution
Knowledge Check
In first figure a meter stick, half of which is wood and the other half steel is pivoted at the wooden end at A and a force is applied at the steel and at O. On second figure the stick is pivoted at the steel end at O and the same force is applied at the wooden end at A. The angular acceleration.
 .Ain first is greater than in secondBequal in both first and secondCin second is greater than in firstDNone of the above.
.Ain first is greater than in secondBequal in both first and secondCin second is greater than in firstDNone of the above.A particle is at a distance r from the axis of rotation. A given torque τ produces some angular acceleration in it. If the mass of the particle is doubled and its distance from the axis is halved, the value of torque to produce the same angular acceleration is -
Aτ/2BτC2τD4τA particle of mass M and radius of gyration K is rotating with angular acceleration α. The torque acting on the particle is
A12MK2αBMK2αCMK2αD14MK2α2
Torque acting on a rotating body
View SolutionA meter stick, half of which is wood and the other half steel, is pivoted at the wooden end and same force isapplied to the steel end. Next, it is pivoted at the steel end and the same force is applied at the wooden end. Does one getthesame angular acceleration in eachcase ? Explain
View SolutionCompute the angular acceleration of a wheel having moment of inertia 20kgm2, when a torque of 10Nm is applied on the wheel.
View SolutionA particle of mass M and radius of gyration K is rotating with angular acceleration α. The torque acting on the particle is
View SolutionA ring and a disc of different masses are rotating with the same kinetic energy. If a retarding torque (τ) is applied to the ring, the ring stops after completing n rotations. If the same retarding torque is applied to the disc, how many rotations would it complete before coming to rest?
View Solution
