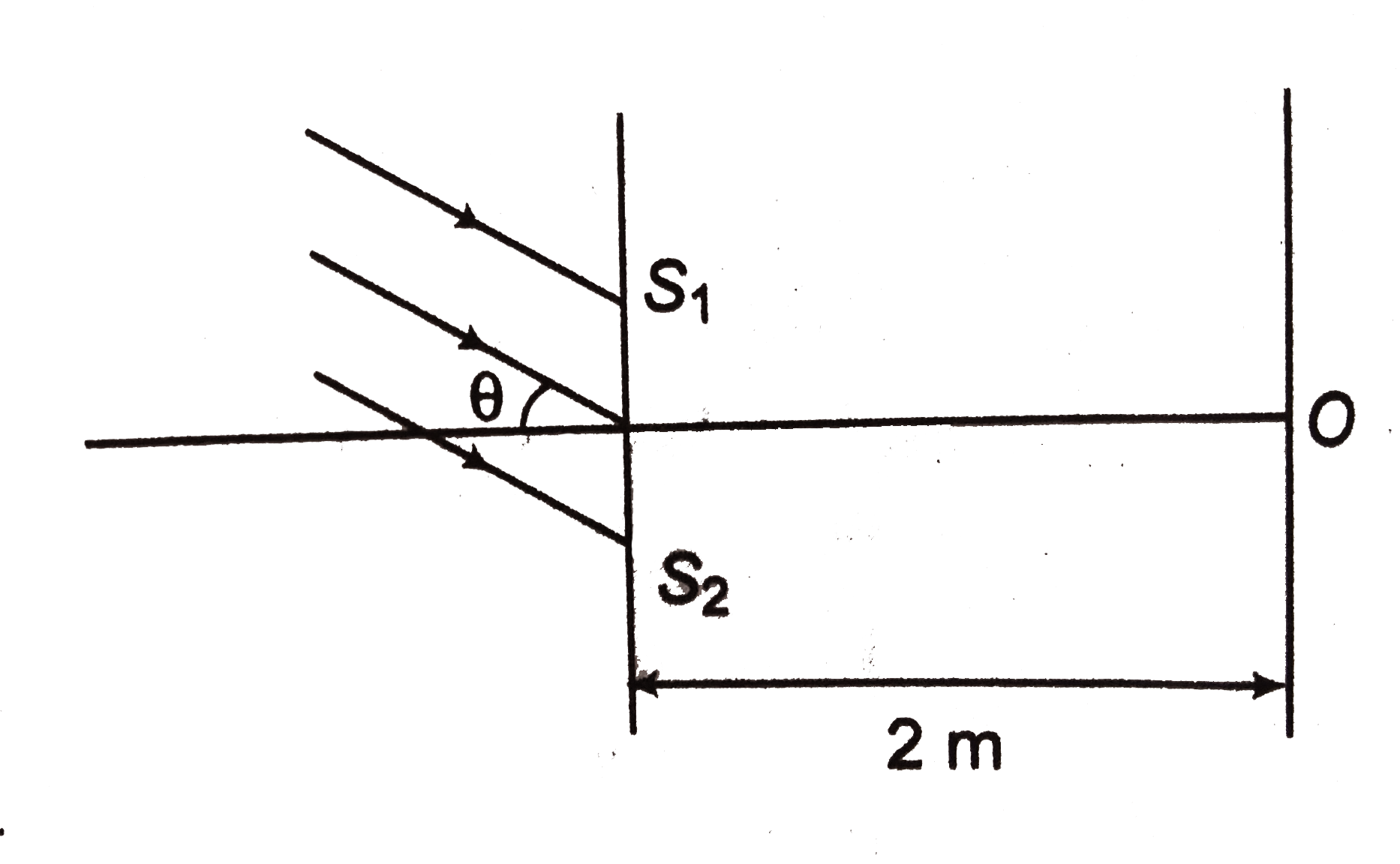
In the figure shown, a parallel beam of light (of wavelength λ1 in
medium μ1) is incident at an angle θ. Distance S1O=S2O. Distance between the
slits is d.
 <br>Usingd=1mm,D=1m,theta = 30^@,lambda_1 = 0.3mm, mu_1 = 4//3andmu_2= 10//9,f∈d<br>(a)they−c∞rd∈ateofthep∮wherethe→talphased⇔erencebetweenthe∫erfer∈g<br>wavesiszer⊙<br>(b)Ifthe∫ensitydue→eachlightwaveatp∮OisI_0, then find the resultant intensity
<br>Usingd=1mm,D=1m,theta = 30^@,lambda_1 = 0.3mm, mu_1 = 4//3andmu_2= 10//9,f∈d<br>(a)they−c∞rd∈ateofthep∮wherethe→talphased⇔erencebetweenthe∫erfer∈g<br>wavesiszer⊙<br>(b)Ifthe∫ensitydue→eachlightwaveatp∮OisI_0, then find the resultant intensity
at O.
Find y-coordinate of the nearest maxima above O.
The correct Answer is:A, B
(a)Wavelength of light in air,
λ0=μ1λ1=0.4mm
Wavelength of light in medium-2,
λ2=λ0μ2=0.4(10/9)=0.36mm
Let net path difference at some angle alpha is zero, then
Δϕ1+Δϕ2=0
or2pi/lambda_1 (Deltax_1) + 2pi/lambda_2 (Deltax_2) = 0 <br>or Deltax_1/lambda_1+Deltax_2/lambda_2=0<br>or ((d sin theta)/lambda_1) + (d sin alpha)/lambda_2 = 0 <br> sin alpha = - lambda_2/lambda_1sin theta <br> = - 0.36/0.4 xx 1/2 = - 0.45<br> :. alpha ~~ -26.74^@ <br> y= D tan alpha <br> = (1m) tan (-26.74^@)<br> ~~ -1/2m.<br>(b)AtO,≠tphased⇔erence,<br> Delta phi or phi = ((2pi)/lambda_1) Deltax_1 <br>=(2pi)/lambda_1 (d sin theta) <br> = (2pi)/0.3 (1) sin 30^@ <br>=(10pi)/3 = 600^@<br>Usingtheequation I=4 I_0 cos^(2) phi/2,wehave<br>I = 4 (I_0) cos^(2)(300^@)<br>=I_0<br>(c)AtO,phased⇔erenceDeltaphi_1is(10pi)/3whichisgreaterthan 2pibut≤ssthan4pi.So,→makeit4pi,<br>weμsthave<br>Delta phi_1 + Deltaphi_2 = 4pi<br>Deltaphi_2 =4pi - (10pi)/3=(2pi)/3<br> Deltaphi_2 = (2pi)/3 = (2pi)/lambda_2 (Deltax_2) = (2pi)/lambda_2(d sin alpha)<br>orsinalpha = lambda_2/(3d)=0.36/(3xx1) = 0.12<br>:. alpha ~~ 6.89^(@)<br>Now,y=D tan alpha<br>=(1m)tan(6.89^@)
=0.12m.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 3
2 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - type-3
1 Video
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 1
2 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
In the figure , if a parallel beam of white light is incident on the plane of the slits S1andS2 then the distance of the nearest white spot on the screen from O is [ Assume D>>d,d>>λ ]
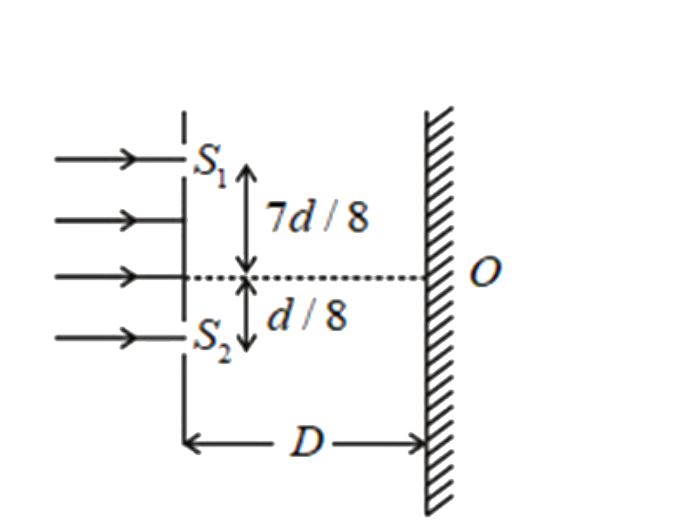
View SolutionIn a YDSE, D = 1m, d = 1mm and λ=1/2mm
Find the no of maxima and minima obtained on the screen.
View Solution
Knowledge Check
In the figure an arrangement of young's double slit experiment is shown. A parallel beam of light of wavelength 'λ' (in medium n1) is incident at an angle 'θ' as shown. Distance S1O=S2O. Point 'O' is the origin of the coordinate system. The medium on the left and right side of the plane of slits has refractive index n1 and n2 respectively. Distance between the slits is d. The distance between the screen and the plane of slits is D.
Using D=1m,d=1mm,θ=30∘,λ=0.3mm,n1=43,n2=109, answer the following

If the intensity due to each light wave at point 'O' is I0 then the resultant intensity at point 'O' will be -AZeroB2I0(1+cos(40π)9)C3I0DI0In the figure an arrangement of young's double slit experiment is shown. A parallel beam of light of wavelength 'λ' (in medium n1) is incident at an angle 'θ' as shown. Distance S1O=S2O. Point 'O' is the origin of the coordinate system. The medium on the left and right side of the plane of slits has refractive index n1 and n2 respectively. Distance between the slits is d. The distance between the screen and the plane of slits is D.
Using D=1m,d=1mm,θ=30∘,λ=0.3mm,n1=43,n2=109, answer the following
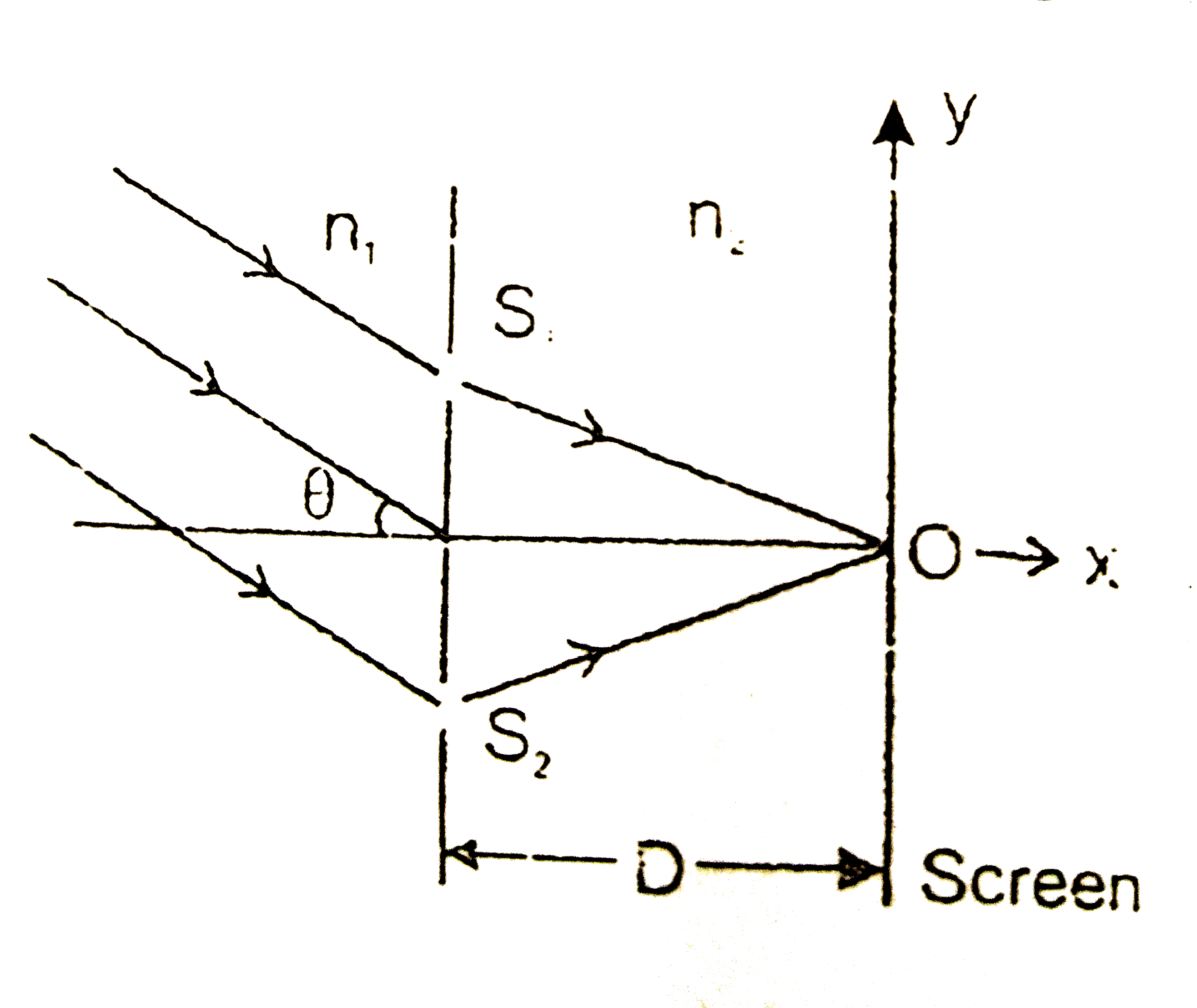
They-corrdinate of the point where the total phase difference between the interefering waves is zero, isAy=0By=+34mCy=−34mD−1√3A light of wavelength 500 nm is incident on a young's slit. The distance between slits annd screen is D=1.8m and distance between slits is d=0.4 mm. if screen moves with s speed 4m/s, with what speed first maxima will move?
Aa. 5mm/sBb.4mm/sCc.3mm/sDd.2mm/s
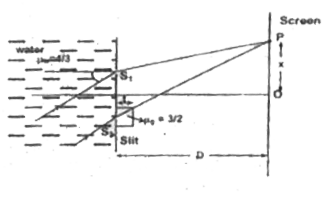
A coherent beam light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1 m from the slits and the separation between- the slits is 3×10−4m. A thin film of glass μg= 3/2 and thickness 0.41 mm is placed near one slit as shown in the figure, find
(a) the position of central maxima.
(b) the intensity at'point O.
View SolutionIn YDSE with d=1mm and D=1m, Slabs of (t=1μm,μ=3) and (t=0.5μm,μ=2) are introduced in front of upper and lower slits, respectively. Find the shift in the fringe pattern.
View SolutionA coherent parallel beam of microwaves of wavelength A = 0.5 mm fails on a Young's double slit apparatus. The separation between maxima is measured on a screen placed paraiiei to the plane, of the slits at a distance of 1.0 m from it as shown in figtird. The separation between the slits is 2d - 1mm.
(a) If the incident beam fails normally on the double slit apparatus, find the y-coordinates of all the interface minima of the screen.
(b) If the incident beam makes an angle of 30° with the x-axis (as shown in fig. find the y-coordinates of the first minima on either side of the central maximum.

View SolutionA parallel beam of light (λ=5000Å) is incident at an angle θ=30∘ with the normal to the slit plane in a Young's double slit experiment. The intensity due to each slit is I_0. Point O is equidistant from S1andS2. The distance between slits is 1mm.
View SolutionA beam of light propagating at an angle α1 from a medium 1 to another medium 2 at an angle α2. If the wavelength of light in medium 1 is λ1. The wavelength of light in medium 2, (λ2, is
View Solution