Prove that for spherical mirrors the product of the distance of the object and the image to the
principal focus is always equal to the square of the principal focal length.
Video Solution
Text Solution
The correct Answer is:A, B, C, D
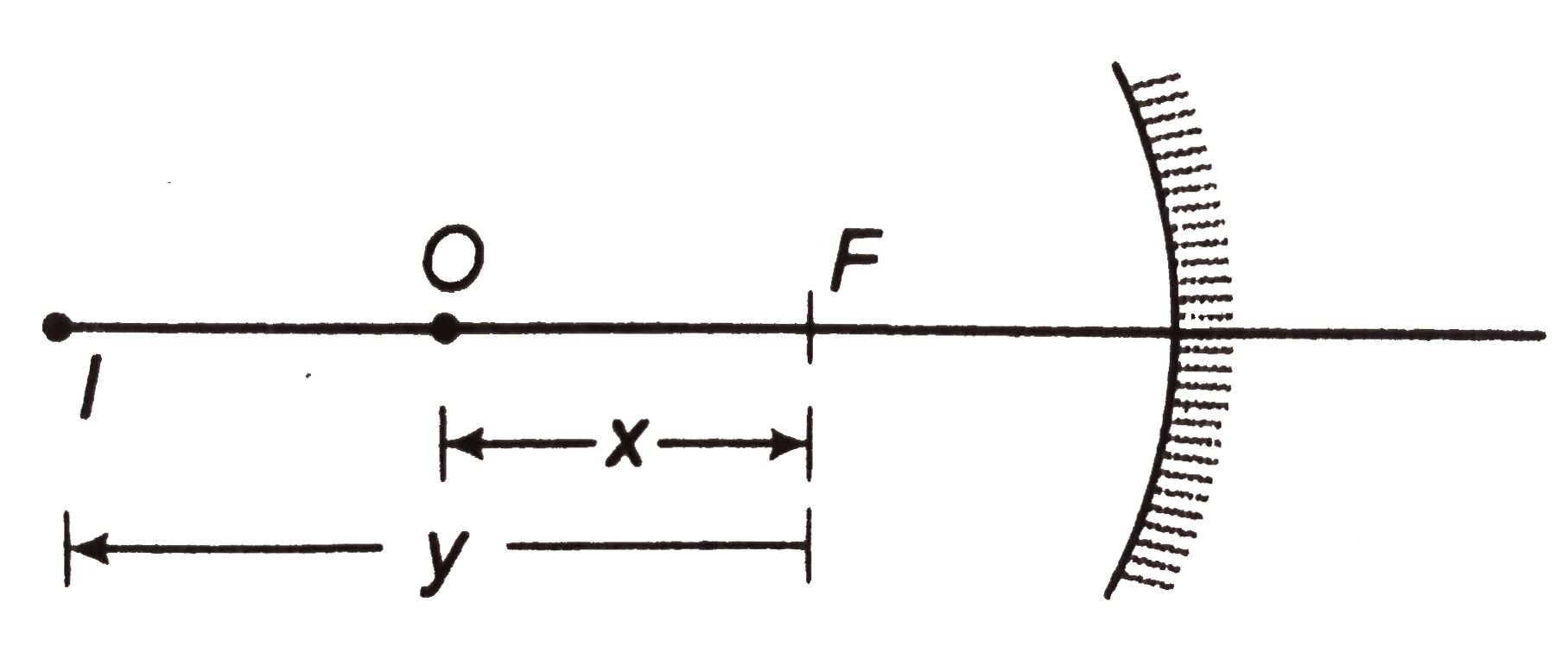
Using 1v+1u=1f
∴1−(y+f)+1−(x+f)=1−f
Solving this equation , we get
xy=f2.
|
Topper's Solved these Questions
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 Single Correct
16 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 More Than One Correct
6 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Objective
12 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
Knowledge Check
The distance of an object from a spherical mirror is equal to the focal length of the mirror. Then the image.
Amust be at infinityBmay be at infinityCmay be at the focusDnoneThe distance of an object from a spherical mirror is equal to the focal length of the mirror. Then the image:
Amust be at infinityBmay be at infinityCmay be at the focusDnoneThe focal length of convex tens is f and the distance of an object from the principal focus is x. The ratio of the size of the real image to the size of the object is
AfxBxfCf+xfDff+x
Define the principal focus of a concave mirror.
View SolutionDefine the principal focus of a concave mirror.
View SolutionDefine the principal focus of a concave mirror.
View SolutionThe distance between the principal focus and centre of curvature of the convex mirror is equal to ___
View SolutionThe magnificationof the image when an object is placed at a distance x from the principle focus of a mirror of focal length f is
View Solution