Two plane mirrors are inclined to each other at an angle θ. A ray of light is reflected at one
mirror and then at the other. Find the total deviation of the ray.
To find the total deviation of a ray of light reflected by two inclined plane mirrors at an angle θ, we can follow these steps:
1. Understanding the Setup:
- We have two plane mirrors inclined at an angle θ.
- A ray of light strikes the first mirror and is reflected to the second mirror.
2. Identify Angles of Incidence and Reflection:
- Let the angle of incidence at the first mirror be i.
- According to the law of reflection, the angle of reflection r will also be i.
3. Determine the Angles Formed:
- The angle between the normal to the first mirror and the incident ray is i.
- The angle between the normal to the first mirror and the reflected ray is also i.
- The angle between the two mirrors is θ.
4. Calculate the Angle at the Second Mirror:
- The angle of incidence at the second mirror will be θ−i (since the total angle at the point of intersection of the two mirrors is 180∘).
- Therefore, the angle of reflection at the second mirror will also be θ−i.
5. Total Deviation Calculation:
- The total deviation D of the ray after reflecting off both mirrors can be calculated as:
D=Deviation due to first mirror+Deviation due to second mirror
- The deviation caused by the first mirror is given by 2i (since it reflects the ray back at an angle of i).
- The deviation caused by the second mirror is given by 180∘−2(θ−i).
6. Combining the Deviations:
- Thus, the total deviation can be expressed as:
D=2i+(180∘−2(θ−i))
- Simplifying this gives:
D=2i+180∘−2θ+2i=4i+180∘−2θ
7. Final Expression for Total Deviation:
- Since the angle of incidence i can be related to the angle θ (specifically, if the ray strikes at a certain angle, we can express it in terms of θ), the total deviation can be simplified further.
- The final expression for the total deviation when the mirrors are inclined at an angle θ is:
D=360∘−2θ
Conclusion
The total deviation of the ray after reflecting off both mirrors is given by:
D=360∘−2θ
- We have two plane mirrors inclined at an angle θ.
- A ray of light strikes the first mirror and is reflected to the second mirror.
- Let the angle of incidence at the first mirror be i.
- According to the law of reflection, the angle of reflection r will also be i.
- The angle between the normal to the first mirror and the incident ray is i.
- The angle between the normal to the first mirror and the reflected ray is also i.
- The angle between the two mirrors is θ.
- The angle of incidence at the second mirror will be θ−i (since the total angle at the point of intersection of the two mirrors is 180∘).
- Therefore, the angle of reflection at the second mirror will also be θ−i.
- The total deviation D of the ray after reflecting off both mirrors can be calculated as:
D=Deviation due to first mirror+Deviation due to second mirror
- The deviation caused by the first mirror is given by 2i (since it reflects the ray back at an angle of i).
- The deviation caused by the second mirror is given by 180∘−2(θ−i).
- Thus, the total deviation can be expressed as:
D=2i+(180∘−2(θ−i))
- Simplifying this gives:
D=2i+180∘−2θ+2i=4i+180∘−2θ
- Since the angle of incidence i can be related to the angle θ (specifically, if the ray strikes at a certain angle, we can express it in terms of θ), the total deviation can be simplified further.
- The final expression for the total deviation when the mirrors are inclined at an angle θ is:
D=360∘−2θ
The total deviation of the ray after reflecting off both mirrors is given by:
D=360∘−2θ
Topper's Solved these Questions
- REFLECTION OF LIGHTBook:DC PANDEYChapter:REFLECTION OF LIGHTExercise:Level 2 Single Correct
Explore 16 Videos
- REFLECTION OF LIGHTBook:DC PANDEYChapter:REFLECTION OF LIGHTExercise:Level 2 More Than One Correct
Explore 6 Videos
- REFLECTION OF LIGHTBook:DC PANDEYChapter:REFLECTION OF LIGHTExercise:Exercise Level 1 Objective
Explore 12 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Level 2 Subjective
Explore 21 Videos
Similar Questions
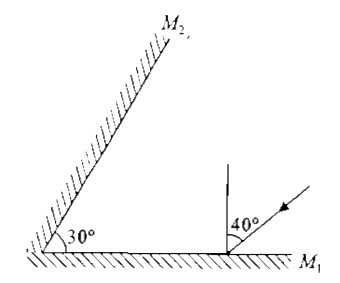
Two plane mirrors are inclined to each other at an angle 30∘ to each other. A ray of light is incident at an angle of 40∘ to the mirror (M1). Find the total angle of deviation of the ray after the third successive due to mirrors.
View SolutionTwo plans mirrors are inclined to each other at some angle .A ray of light incident at 30∘on one,after reflection form the other retraces its path .The angles between the mirrors is:
30∘(2)45∘(3)60∘(4)90∘
View Solution
Knowledge Check
Two plane mirrror are inclined to each other at 70∘. A ray of light is incident on one mirror. They ray after two reflections will undergo a total deviation of :
A180∘B220∘C40∘DCannot be found because angle of incidence is not givenTwo plane mirror are inclined to each other at 90∘. A ray of light is incident on one mirror. The ray will undergo a total deviation of
A180∘B90∘C45∘Ddata insufficientTwo vertical plane mirrors are inclined at an angle of 60∘ with each other. A ray of light travelling horizontally is reflected first from one mirror and then from the other. The resultant deviation is
A60∘B120∘C180∘D240∘
Two plane mirrors are inclined to each other at a certain angle.A ray of light first incident on one of them at an inclination of 10∘ with the mirror retraces its path after five reflections.The angle between the mirrors is
View SolutionTwo plane mirrors are inclined to each other with their reflecting daces making acute angle. A light ray is incident on one plane mirror. The total deviation after two successive reflections is :
View SolutionTwo plane mirros are inclined to each other at an angle 60∘ if a ray of light incident on firs tmirros paralell to the second mirror, it is reflected formt the second mirror
View SolutionTwo plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. The angle between the two mirrors is :
View SolutionTwo plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. The angle between the two mirrors is :
View Solution
