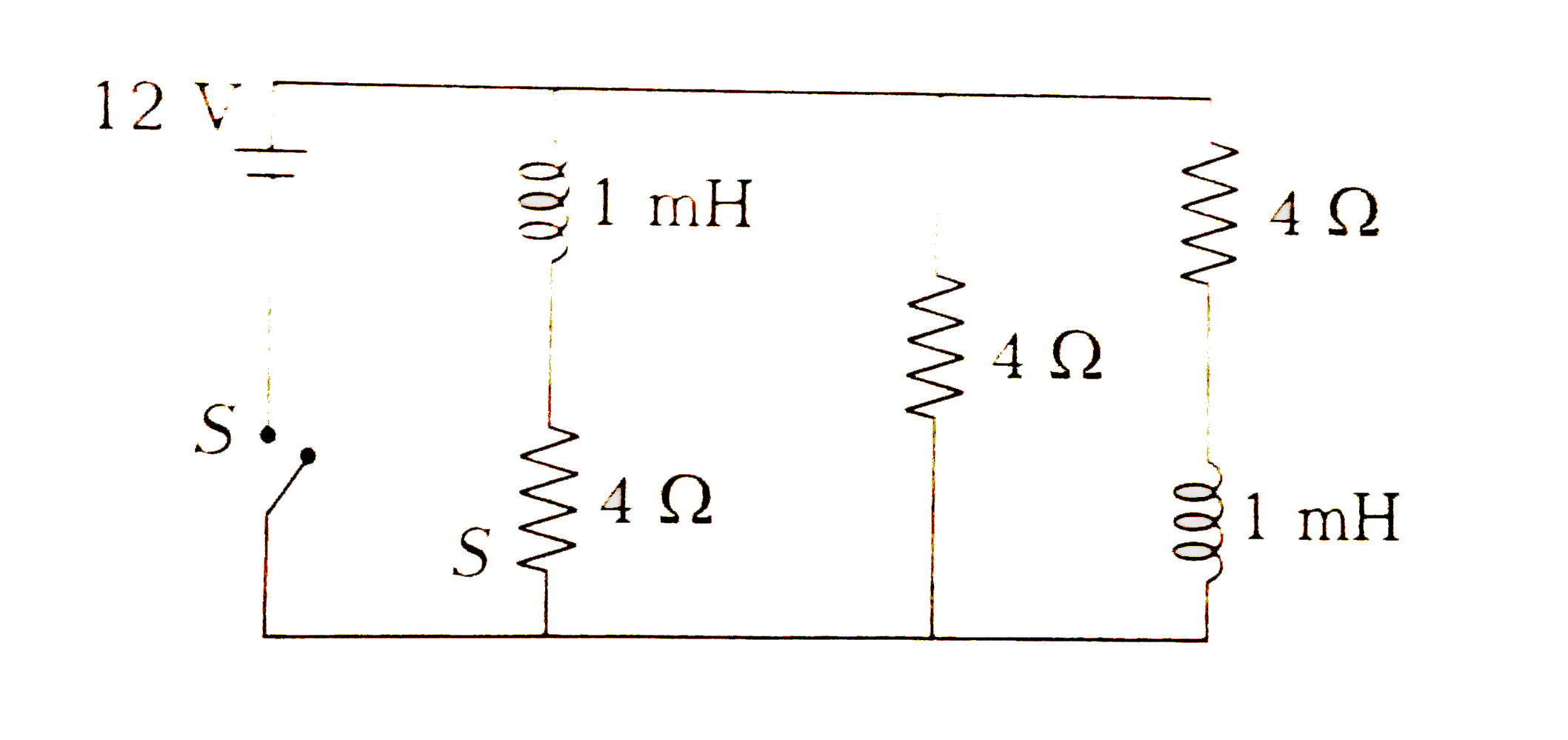A 35.0V battery with negligible internal resistance, a 50.0Ω resistor, and a 1.25mH inductor with negligible resistance are all connected in series with an open switch. The switch is suddenly closed
(a) How long after closing the switch will the current through the inductor reach one-half of its maximum value?
(b) How long after closing the switch will the energy stored in the inductor reach one-half of its maximum value?
The correct Answer is:C
a. After one half life,
t=t1/2=(ln2)τL
=0.693LR
=(0.693)(1.25×10−3)50
=1.73×10−5s
b. (12Li2)=(12Li20)/2
∴i=i0√2
Now, apply
i=i0(1−e−t/τL)
where τL=LR
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Single Correct
37 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions
3 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
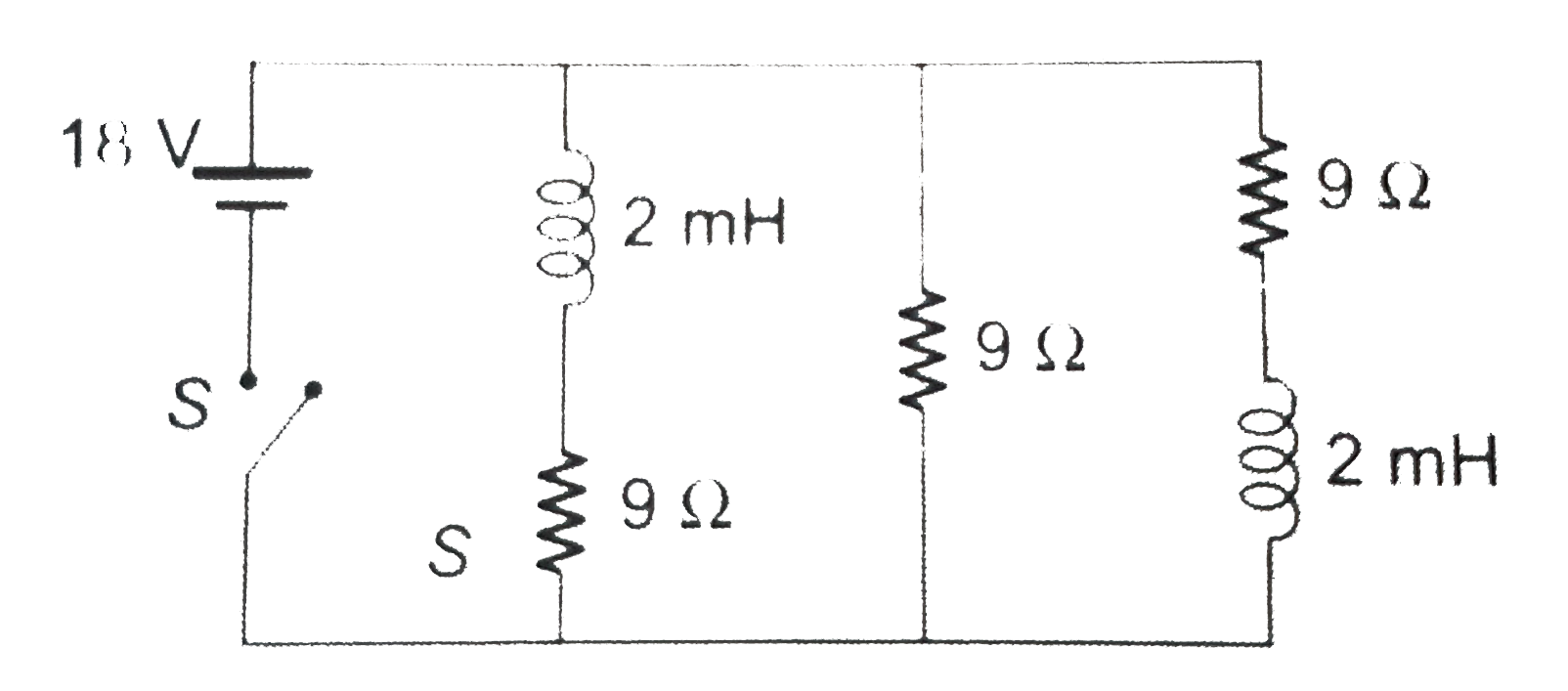
In the circuit as shown in figure the switch is closed at t=0.

A long time after closing the switchAvoltage drop across the capacitor is EBcurent through the battery is E/R1+R2Cenegru stores in the capacitor is
12C(R2ER1+R2)2Dcurrent through the capacitor becomes zeroRefer to Fig. 7.49.
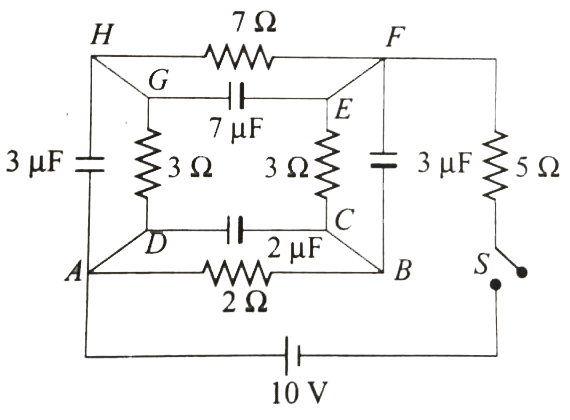
At t=0 , the switch is closed . Just after closing the switch, find the current through the 5Ω resistor.A45AB25AC65AD2ARefer to Fig. 7.49.
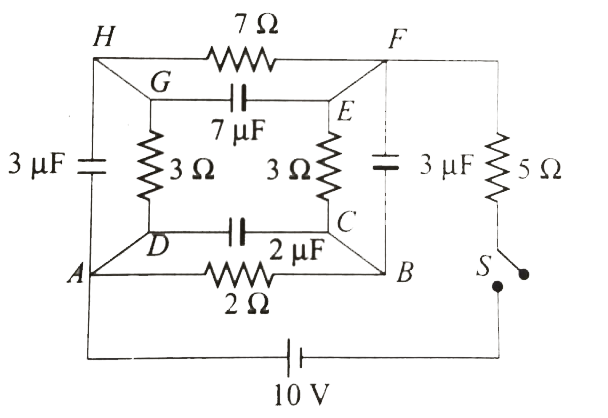
Long time after closing the switch , find the current through the 5Ω resistor.A45AB25AC65AD85A
shows three resistances are
connected with switch S initially the switch is open. When
the switch S is closed find the current passed through it.
View SolutionAn inductor L and a resistance R are connected in series with a battery of emf E and a switch. Initially the switch is open. The switch is closed at an instant t = 0. Select the correct alternatives
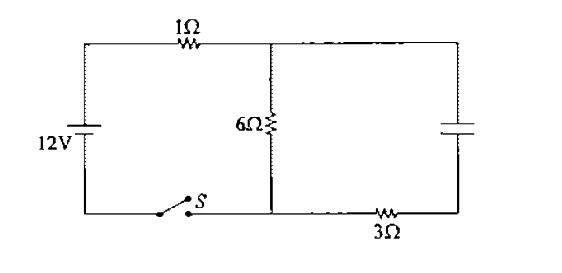
View SolutionIn the circuit shown in figure-3.348 when the switch is closed, the initial current through the 1Ω resistor just after closing the switch is
View SolutionSolenoid of self-inductance L is connected in series with a resistor of resistance R with a battery and switch. Switch is closed at t = 0. How much time will be taken by inductor to acquire one-fourth of its maximum energy?
View SolutionAssertion In the figure, just after closing the switch the potential drop across inductor is maximum.
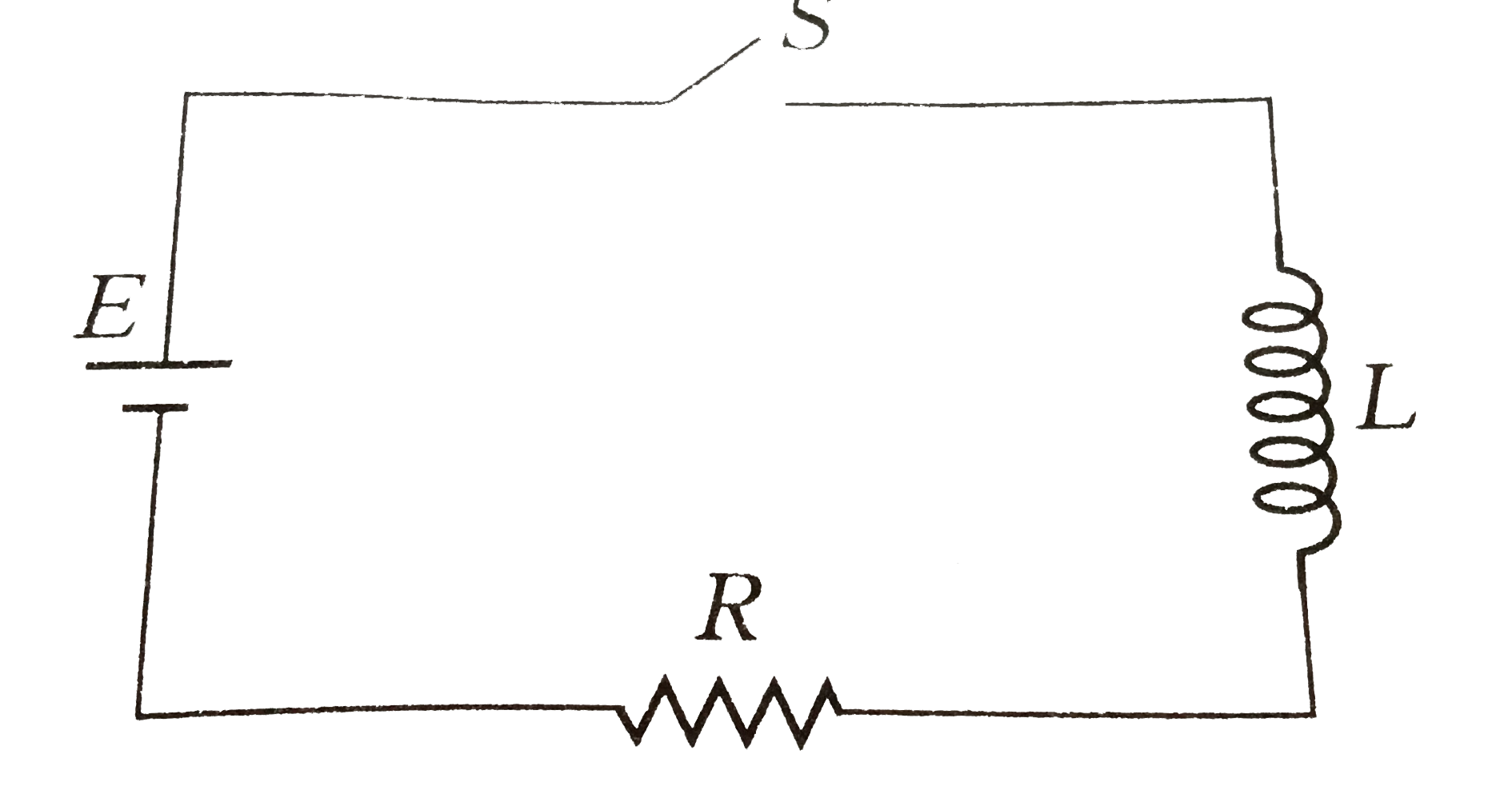
Reason The rate of change of current just after closing the switch is maximum.
View Solution