A battery of emf and of negligible internal resistance is connected in a circuit as shown in figure. The inductor has a piece of soft iron inside it. When steady state is reached in the piece of soft iron is abruptly pulled out suddenly so that the inductance of the inductor decreases to with with battery remaining connected. Calculate.
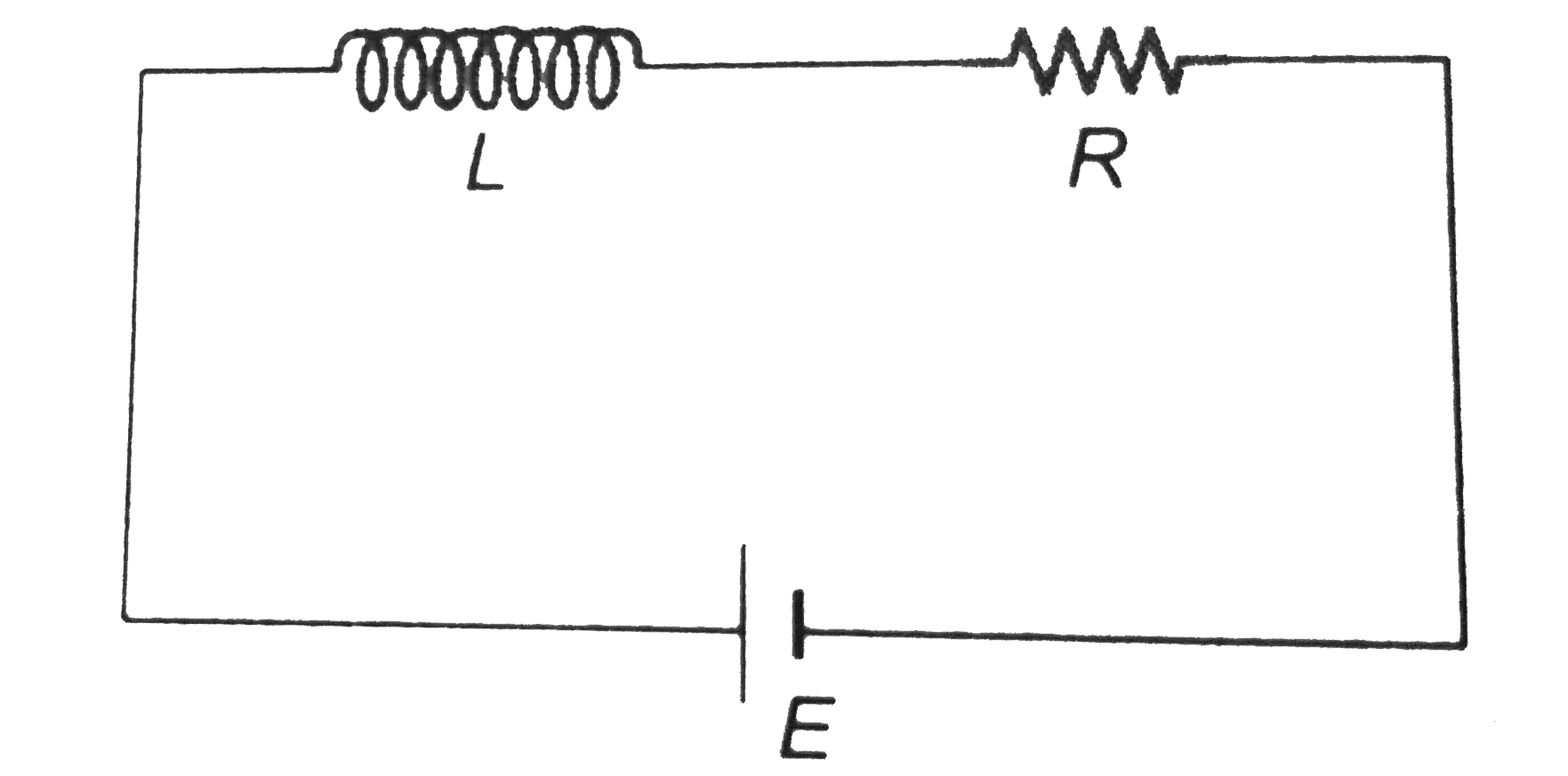
a. Current as a function of time assuming at the instant when piece is pulled.
b. the work done to pull out the piece.
c. thermal power generated in the circuit as as function of time.
d. power supplied by the battery as a function of time.
HOW TO PROCEED When the inductance of an inductor is abruptly changed, the flux passing through it remains constant.
constant
constant
a. At time steady state current in the circuit is . Suddenly , reduces to , so current in the circuit at time will increase to . Let i be the current at time .
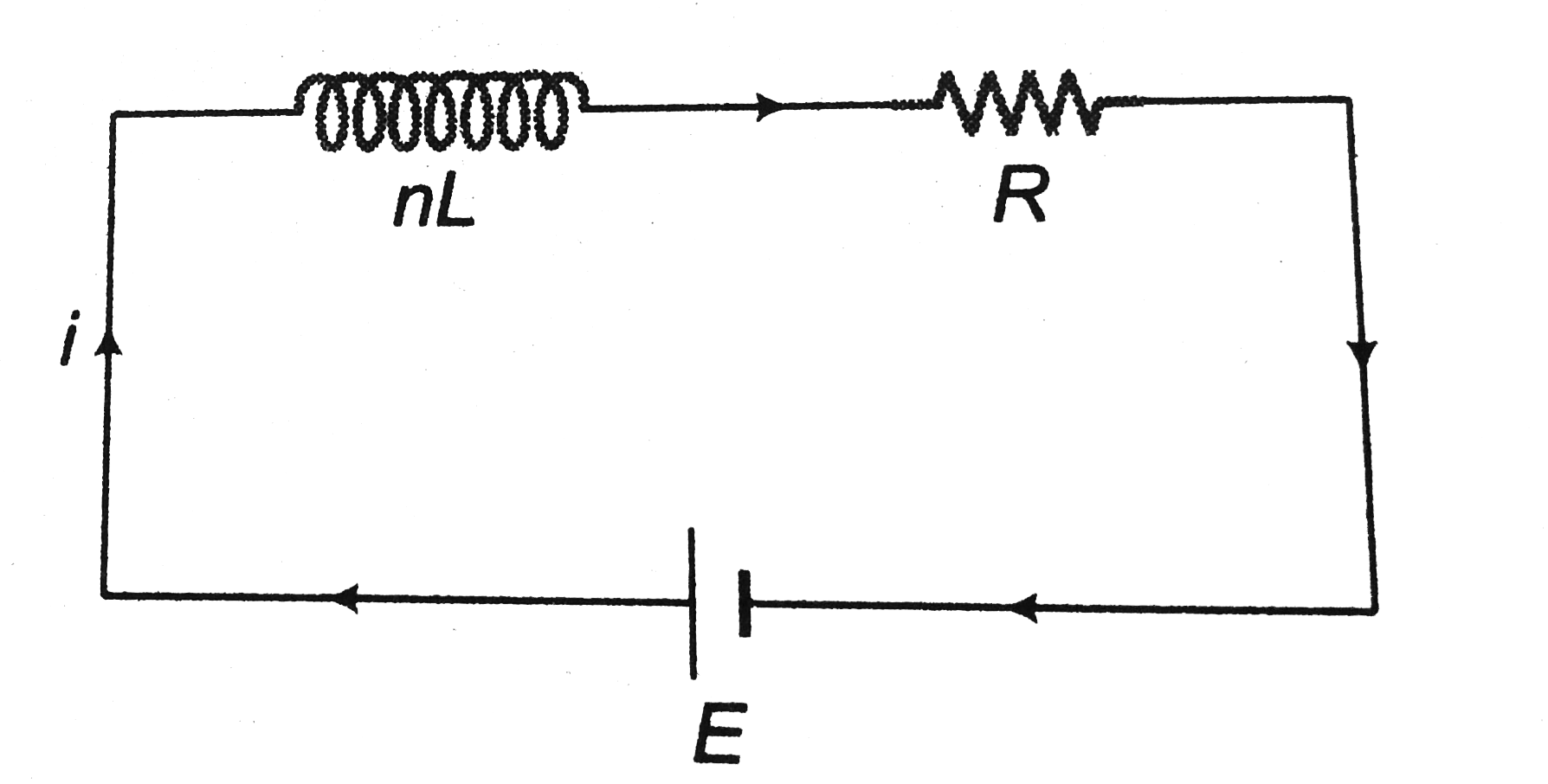
Applying Kirchoff's loop rule, we have
solving this equation we get
Here,
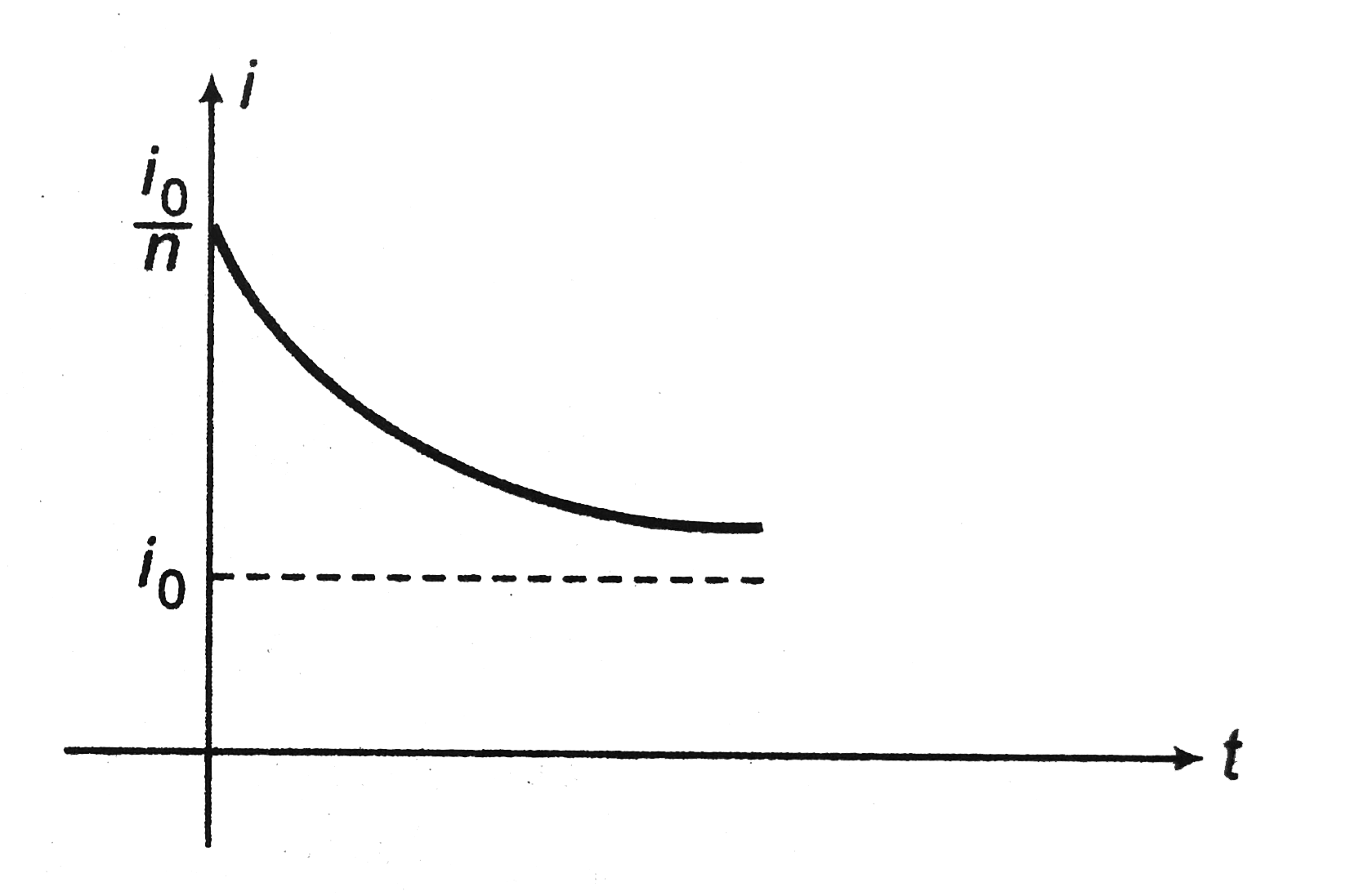
Form the i-t equation we get at and at
The graph is as known in figure.
At , current in the circuit is . Current in the circuit in steady state will be again . So, it will decrease exponentially from to . From the graph, the equation can be fomed without doing any calculation.
 <math xmlns=) :. i=i_0+(i_0/n-i_0)e^(-t//tau_L)W=U_f-U_i=1/2L_fi_f^2-1/2L_(i)i_(i)^(2)=(1)/(2)(nL) ((E)/(nR))^(2) -(1)/(2)(L) ((E)/(R))^(2)=1/2L(E/R)^2(1/n-1)=1/2L(E/R)^2((1-n)/n)P_1=i^2RP_2=Ei
:. i=i_0+(i_0/n-i_0)e^(-t//tau_L)W=U_f-U_i=1/2L_fi_f^2-1/2L_(i)i_(i)^(2)=(1)/(2)(nL) ((E)/(nR))^(2) -(1)/(2)(L) ((E)/(R))^(2)=1/2L(E/R)^2(1/n-1)=1/2L(E/R)^2((1-n)/n)P_1=i^2RP_2=Ei
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise 27.1
Explore 8 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise 27.2
Explore 4 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Example Type 6
Explore 3 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
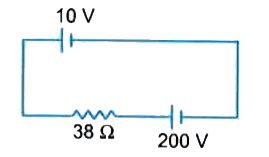
A 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Oemga as shown in figure.
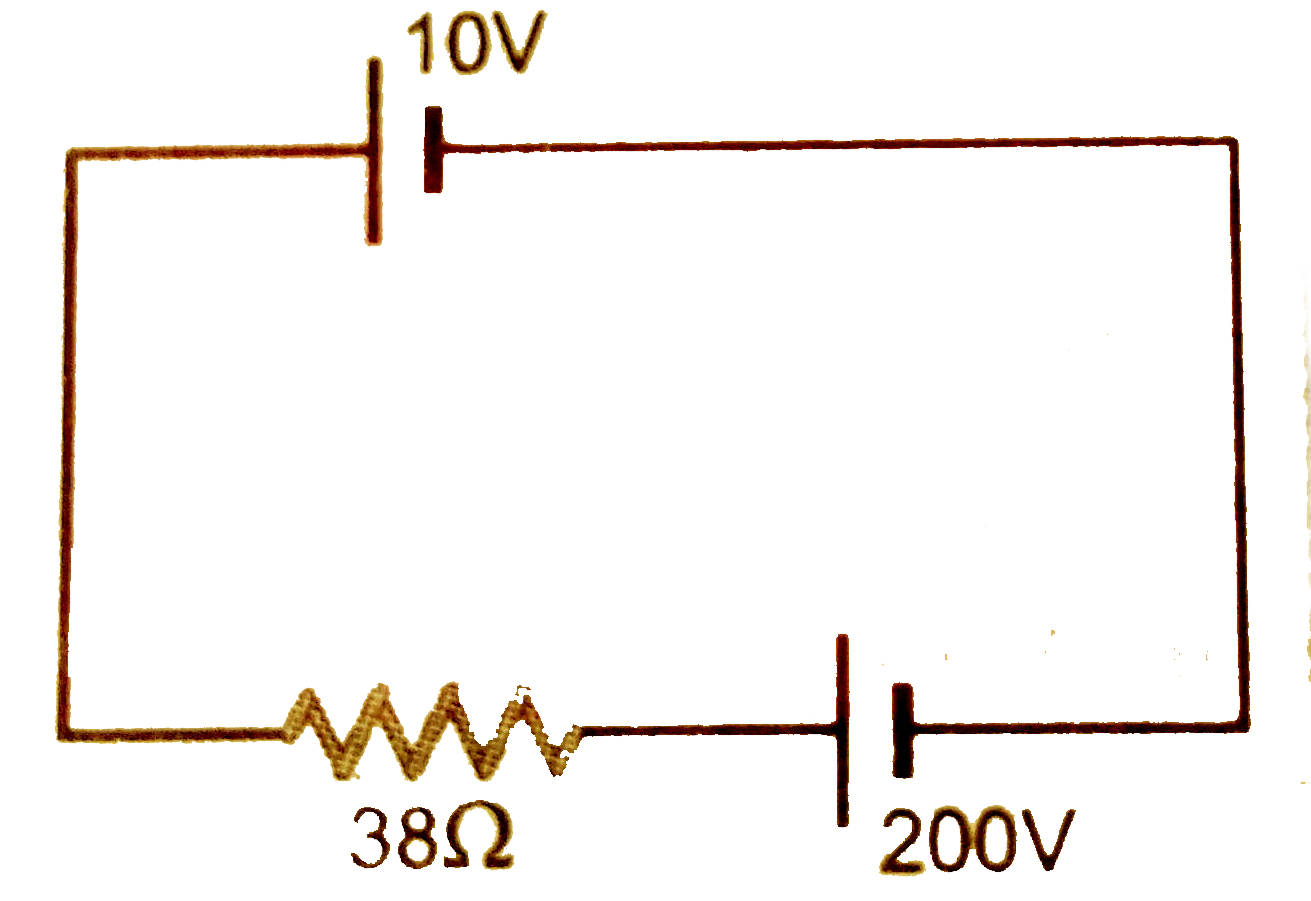 . Find the value of current in the circuit.
. Find the value of current in the circuit.
View Solution
Knowledge Check
A 3 volt battery with negligible internal resistance is connected in a circuit as shown in the figure. The current I, in the circuit will be
 A1AB1.5AC2AD1/3A
A1AB1.5AC2AD1/3AA battery of emf E and internal resistance r is connected to a variable resistor R as shown in figure. Which one of the following is true ?
 APotenital difference across the terminals of the battery is maximum, when R=rBPower delivered to the resistor is maximum when R=rCCurrent in the circuit is maximum when R=rDCurrent in the circuit is maximum when R>>r
APotenital difference across the terminals of the battery is maximum, when R=rBPower delivered to the resistor is maximum when R=rCCurrent in the circuit is maximum when R=rDCurrent in the circuit is maximum when R>>rA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
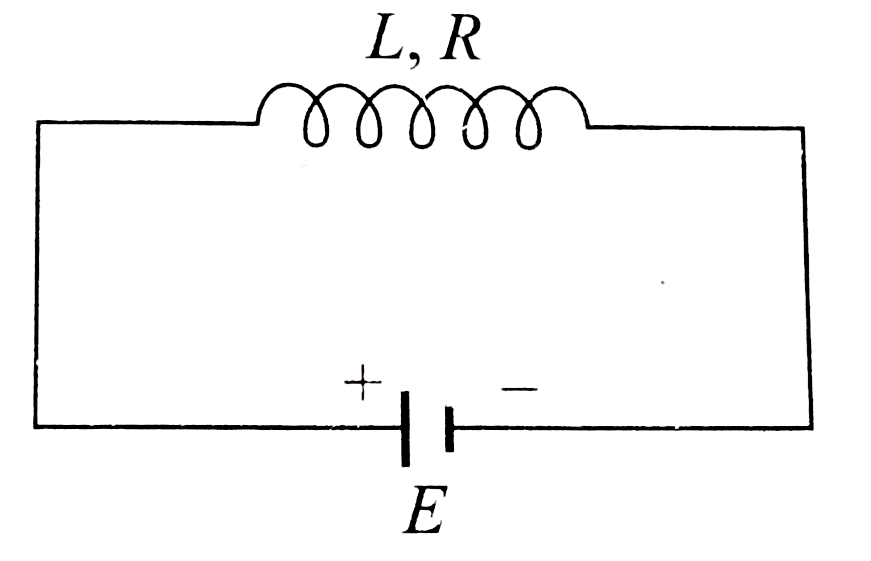
Power supplied by the battery as a function of timeAP=E2R[1+(1−1η)e−tλ]BP=E2R[1+(1+1η)e−tλ]CP=E2R[1−(1+1η)e−tλ]DP=E2R[1−(1−1η)e−tλ]
A 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38 Ω as shown in the Fig. Find the value of the current in circuit.
View SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
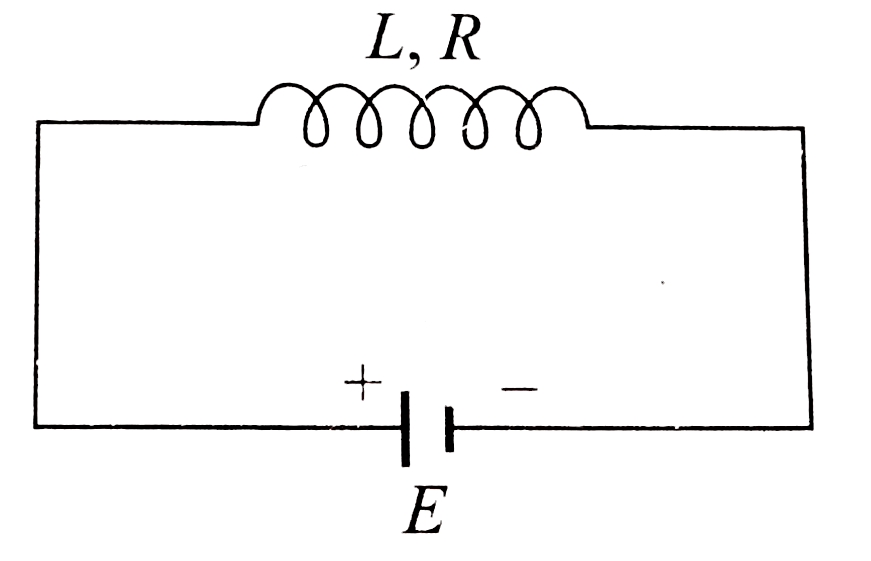
The work done to pull out the soft iron piece is
View SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
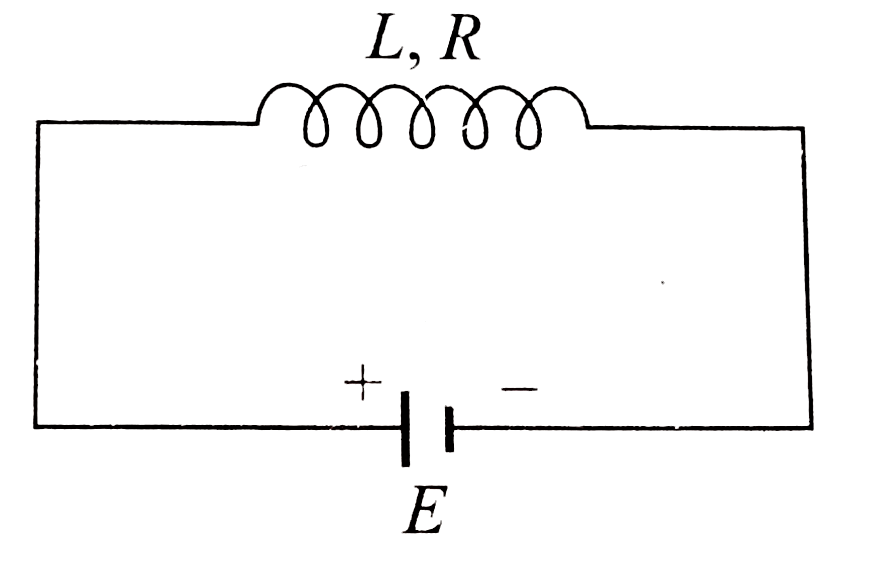
Assume t = 0 is the instant when iron piece has been pulled out, the current as a function of time after this is
View SolutionA battery of e mf 10 V and internal resistance 3Ω is connected to a resistor as shown in the figure. If the current in the circuit is 0.5 A . then the resistance of the resistor will be
View SolutionA battery of emf 10 V and internal resistance 3Ωis connected to a resistor. The current in the circuit is 0.5 A . The terminal voltage of the battery when the circuit is closed is
View Solution

