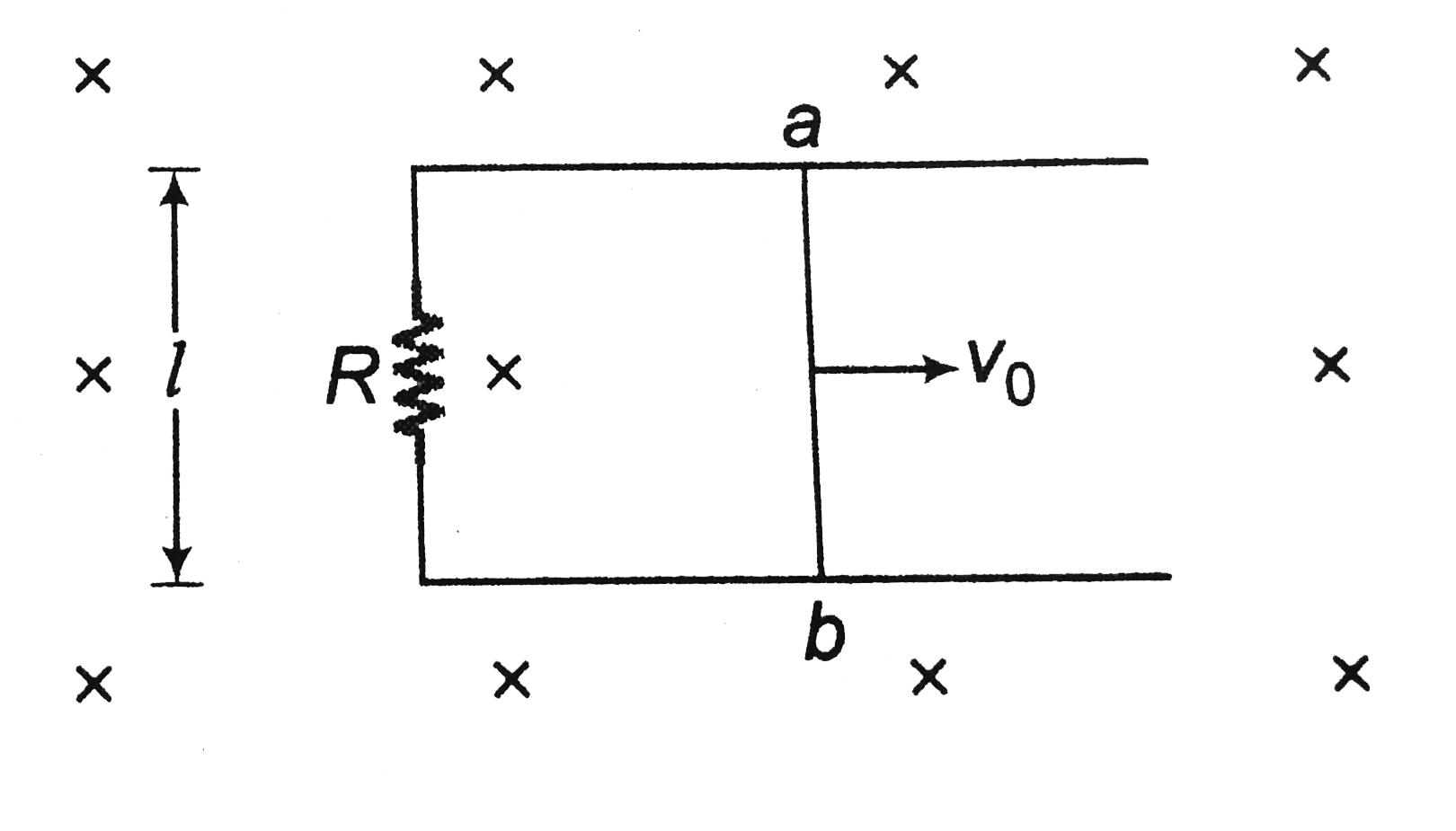
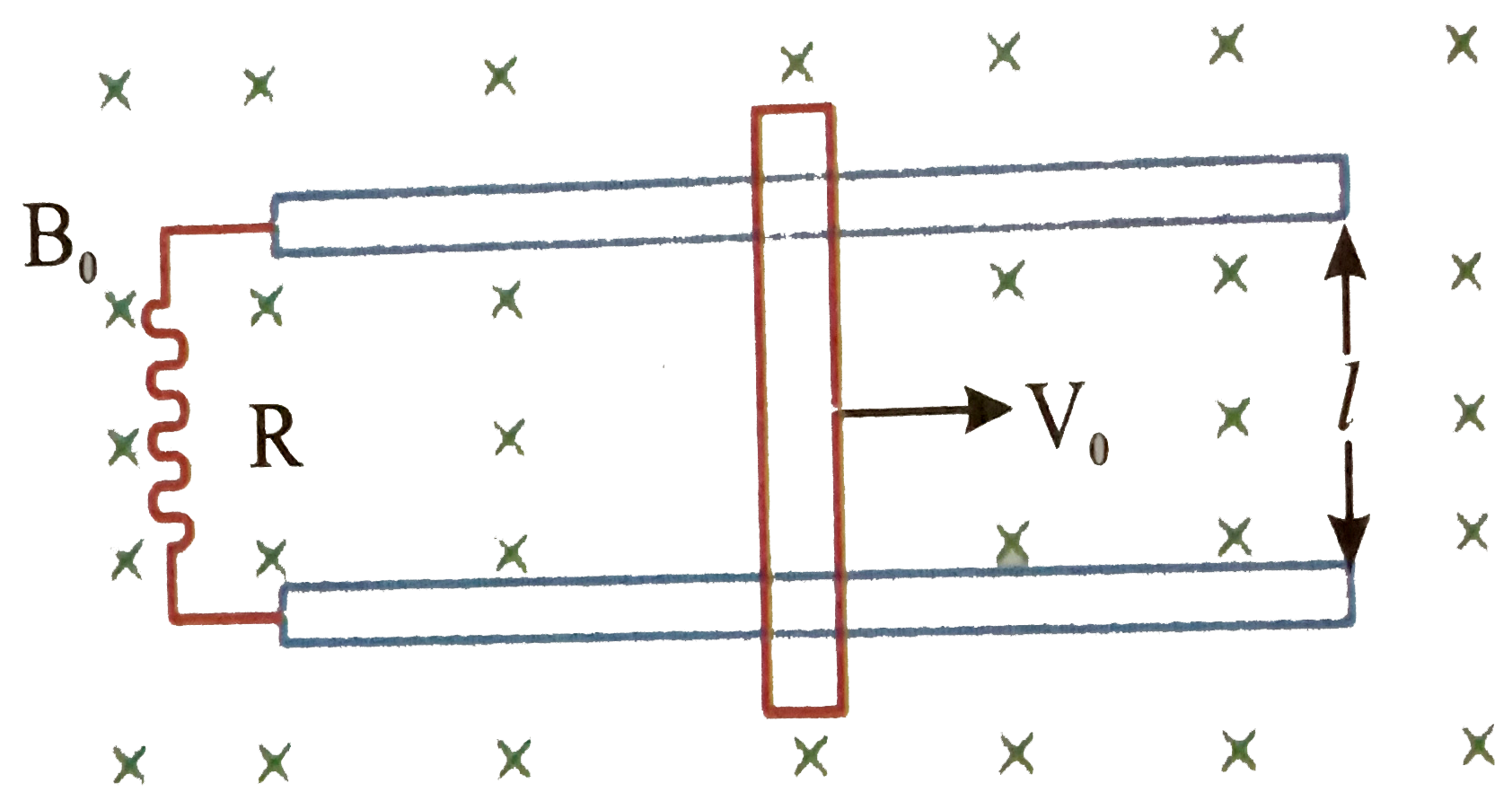
A conducting rod shown in figure of mass m and length l moves on two frictionless horizontal parallel rails in the presence of a unifom magnetic field directed into the page., The rod is given an initial velocity v0 to the right and is released at t=0. Find s a function of time
a. the volocity of the rod
b. the induced current and
c. the magntitude of the induced emf.
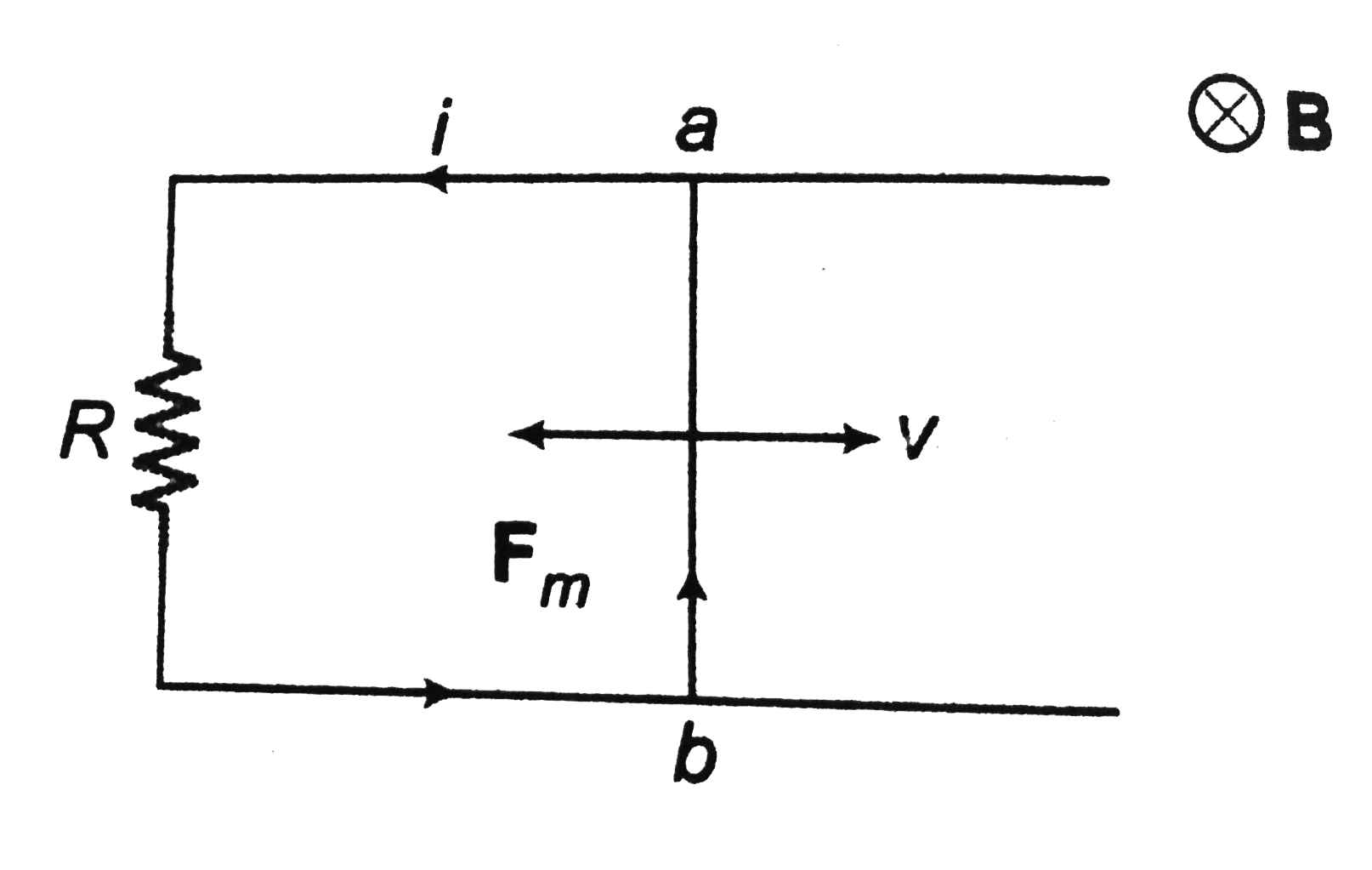
a. Let v be the velocity of the rod at time t
current in the ciruit at his moment is
i=BvlR …..i
From right had rule, we can see that this current is in counterclockwise direction.
The magnetic force is
Fm=−ilB=−B2l2Rv
Hence, negative sign denotes that the force is to the left and retards the motion. This is the only horizontal force acting on the bar, and hence, Newton's second law applied to motion is horizontal direction gives
mdvdt=Fm=−B2l2Rv
∴dvv=−(B2l2mR)dt
Integrating this equation using the initial condition that
v=v0 at t=0, we find that
∫vv0dvv=B2l2mR∫t0dt
Solving this equation we find that
v=v0e−t/τ ...........ii
where ,τ=mRB2l2
This expression indicates that the velocity of the rod decreses expnentially with time under the action of the magnetic retarding force.
b. i=Bvlr
substituting the value of v from Eqn (ii), we get
i=Blv0Re−t/τ
c. eiR=Blv0e−t/τ
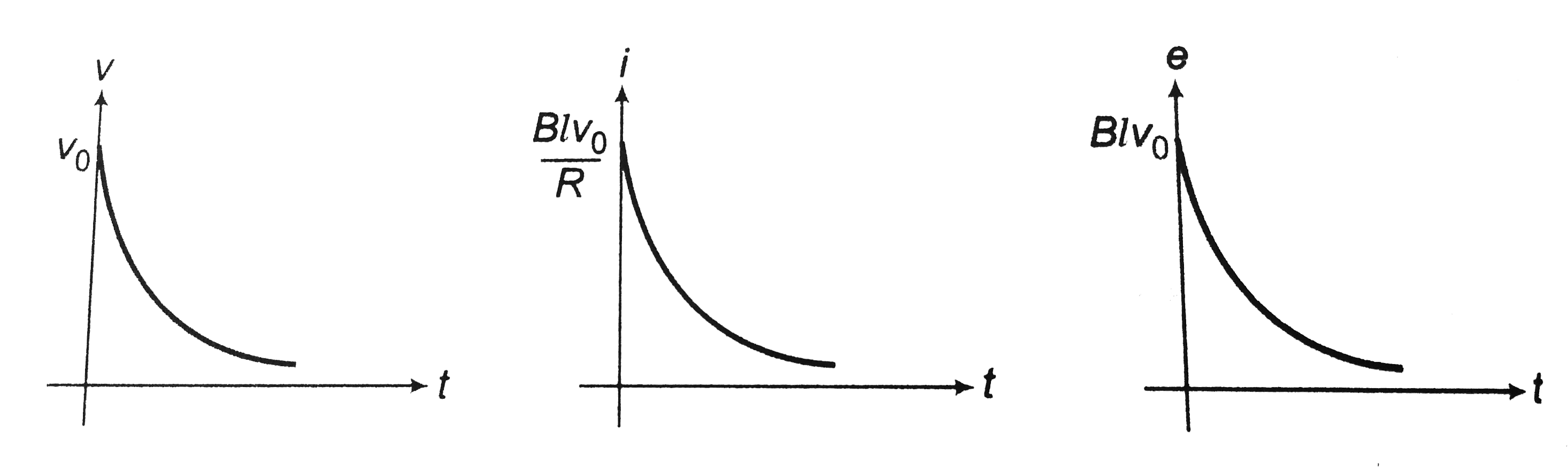
i. and e both decrease exonentially with time v-t, i=t and e-t graphs are as shown in figure.
Alternate solution: This problem can also be solved by energy conservation principle. Let at some instant velocity of the rod is v. As no external force is present. Energy is dissipated in the resistor at the cost of kinetic energy of the rod. Hence,
(−dKdt)= power dissipated in the resistor
or −ddt(12mv2)=e2R
or −mv(dvdt)=B2l2v2R (as e=Bvl)
∴dvv=B2l2mRdt
∴∫vv0dvv=B2l2mRdt
or v=v0e−t/τ, where τ=mRB2l2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.1
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.2
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 6
3 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A bar of mass m and length l moves on two frictionless parallel rails in the presence of a uniform magnetic field directed into the plane of the paper. The bar is given and initial velocity vi to the right and released. Find the velocity of bar, induced emf across the bar and the current in the circuit as a function of time
View SolutionFind the velocity of the moving rod at time t if the initial velocity of the rod is v and a constant force F is applied on the rod.Neglect the resistance of the rod.

View Solution
Knowledge Check
A conducting bar mass m and length l moves on two frictionless parallel conducting rails in the presence of a uniform magnetic field B0 directed into the paper. The bar is given an initial velocity v0 to the right and is released at t=0. The velocity of the bar as a function of time is given by
 Av0×mRtB20l2Bv0e−B20l2tmRCv0×e−2B20l2tmRDv0e−B20l2t2mR
Av0×mRtB20l2Bv0e−B20l2tmRCv0×e−2B20l2tmRDv0e−B20l2t2mRA conducting bar of mass m and length l moves on two frictionless parallel rails in the presence of a constant uniform magnetic field of magnitude B directed into the page as shown in the figure . The bar is given an initial velocity v0 towards the right at t = 0. Then the
 AInduced current in the circuit is in the clockwise directionBVelocity of the bar decreases linearly with timeCDistance the bar travels before it comes to a complete stop is proportional to RDPower generated across the resistance is proportional to l.
AInduced current in the circuit is in the clockwise directionBVelocity of the bar decreases linearly with timeCDistance the bar travels before it comes to a complete stop is proportional to RDPower generated across the resistance is proportional to l.Two idential conductors P and Q are placed on two frictionless rails R and S in a uniform magnetic field directed into the plane. If P is moved in the direction shown in figure with a constant speed, then rod Q
 Awill be attracted towards PBwill be repelled away from PCwill remain stationaryDmay be repelled away orattracted towards P
Awill be attracted towards PBwill be repelled away from PCwill remain stationaryDmay be repelled away orattracted towards P

A uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View Solution
Find the velocity of the moving rod at time t if the initial velocity of the rod is v and a constant force F is applied on the rod. Neglect the resistance of the rod.
View SolutionA glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionA rod of mass M and length l is suspended by two wires P and Q. A uniform magnetic field 'B' is directed into the page. When current through the rod is l. Then the tension in each supporting wire is-
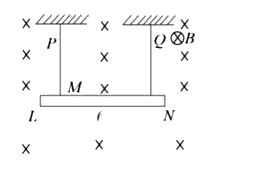
View SolutionTwo long parallel metallic wires with a resistance 'R' from a horizontal plane . A conducting rod AB is on the wires shown in figure . The space has magnetic field pointing vertically downwards. The rod is given an initial velocity 'v0'. There is no friction in the wire and the rod . After a time 't' the velocity v of the rod will be such that :-
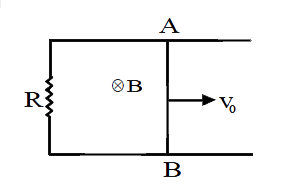
View Solution