A proton of charge e and mass m enters a uniform magnetic field B=Bi with an initial velocity v=vxˆi+vyˆj. Find an expression in unit vector notation for its velocity at time t.
The correct Answer is:A, B
To solve the problem of a proton entering a uniform magnetic field, we can follow these steps:
Step 1: Understand the Given Information
We have a proton with:
- Charge e
- Mass m
- Initial velocity v=vx^i+vy^j
- A uniform magnetic field B=B^i
Step 2: Determine the Force Acting on the Proton
The magnetic force acting on a charged particle moving in a magnetic field is given by:
F=qv×B
For our case:
F=e(vx^i+vy^j)×(B^i)
Since the cross product of parallel vectors is zero:
F=e(vx^i+vy^j)×(B^i)=0+evyB^k=evyB^k
This force acts in the negative z-direction.
Step 3: Analyze the Motion
- The x-component of the velocity vx remains unchanged because there is no force acting in the x-direction.
- The y-component of the velocity will change due to the magnetic force acting on it.
Step 4: Find the Change in Velocity
The acceleration a in the y-direction is given by:
a=Fm=evyBm^k
This indicates that the proton will undergo circular motion in the yz-plane due to the force acting in the z-direction.
Step 5: Determine the Angular Frequency
The angular frequency ω of the circular motion is given by:
ω=qBm=eBm
Step 6: Express the Motion in Terms of Time
The angle θ at time t is given by:
θ=ωt=eBmt
Step 7: Find the Components of Velocity at Time t
- The x-component remains constant:
vx(t)=vx
- The y-component varies with time as:
vy(t)=vycos(eBmt)
- The z-component varies as:
vz(t)=−vysin(eBmt)
Step 8: Combine the Components
The velocity vector at time t can be expressed as:
v(t)=vx^i+vycos(eBmt)^j−vysin(eBmt)^k
Step 9: Final Expression
Thus, the expression for the velocity of the proton at time t in unit vector notation is:
v(t)=vx^i+vycos(eBmt)^j−vysin(eBmt)^k
---
We have a proton with:
- Charge e
- Mass m
- Initial velocity v=vx^i+vy^j
- A uniform magnetic field B=B^i
The magnetic force acting on a charged particle moving in a magnetic field is given by:
F=qv×B
For our case:
F=e(vx^i+vy^j)×(B^i)
Since the cross product of parallel vectors is zero:
F=e(vx^i+vy^j)×(B^i)=0+evyB^k=evyB^k
This force acts in the negative z-direction.
- The x-component of the velocity vx remains unchanged because there is no force acting in the x-direction.
- The y-component of the velocity will change due to the magnetic force acting on it.
The acceleration a in the y-direction is given by:
a=Fm=evyBm^k
This indicates that the proton will undergo circular motion in the yz-plane due to the force acting in the z-direction.
The angular frequency ω of the circular motion is given by:
ω=qBm=eBm
The angle θ at time t is given by:
θ=ωt=eBmt
- The x-component remains constant:
vx(t)=vx
- The y-component varies with time as:
vy(t)=vycos(eBmt)
- The z-component varies as:
vz(t)=−vysin(eBmt)
The velocity vector at time t can be expressed as:
v(t)=vx^i+vycos(eBmt)^j−vysin(eBmt)^k
Thus, the expression for the velocity of the proton at time t in unit vector notation is:
v(t)=vx^i+vycos(eBmt)^j−vysin(eBmt)^k
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
A proton of charge e and mass m enters a uniform magnetic field B=Bi with an initial velocity v=vxˆi+vyˆj. Find an expression in unit vector notation for its velocity at time t.
View SolutionA particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.
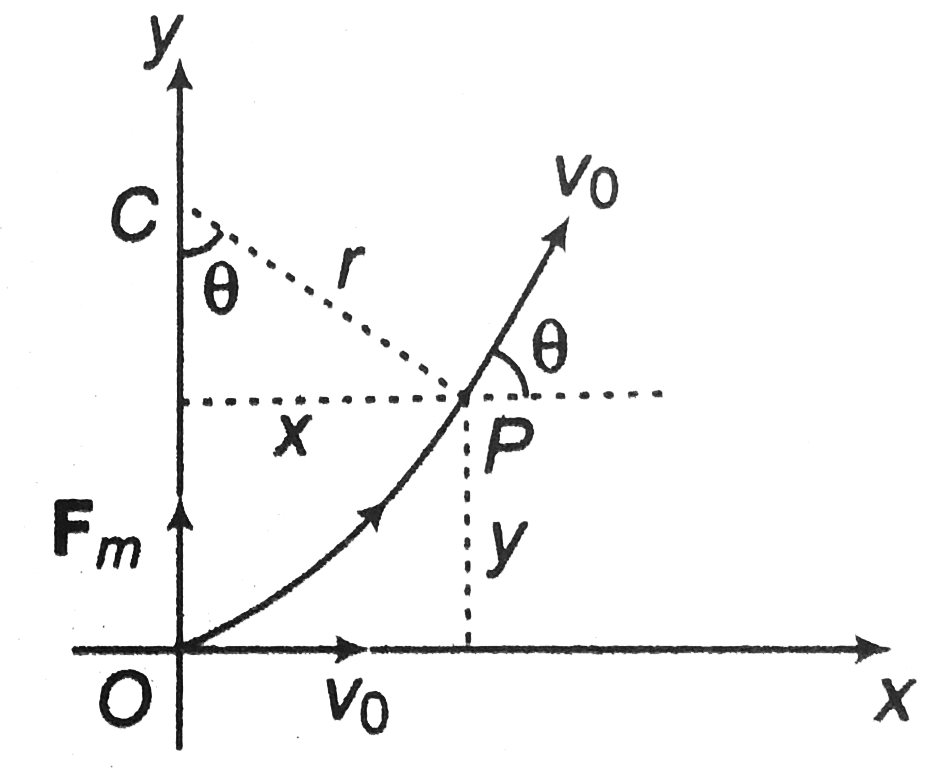
View Solution
Knowledge Check
An electron of charge −e, mass m, enters a uniform magnetic field →B=Bˆi with an initial velocity →v=vxˆi+vyˆj. What is the velocity of the electron after a time interval of t seconds?
Avxˆi+vyˆj+emvyBtˆkBvxˆi+vyˆj−emvyBtˆkCvxˆi+(vy+emvyBt)ˆjD(vx+emvyBt)ˆi+vyˆjA particle of charge -q and mass m enters a uniform magnetic field →B (perpendicular to paper inward) at P with a velocity v0 at an angle α and leaves the field at Q with velocity v at angle β as shown in fig.
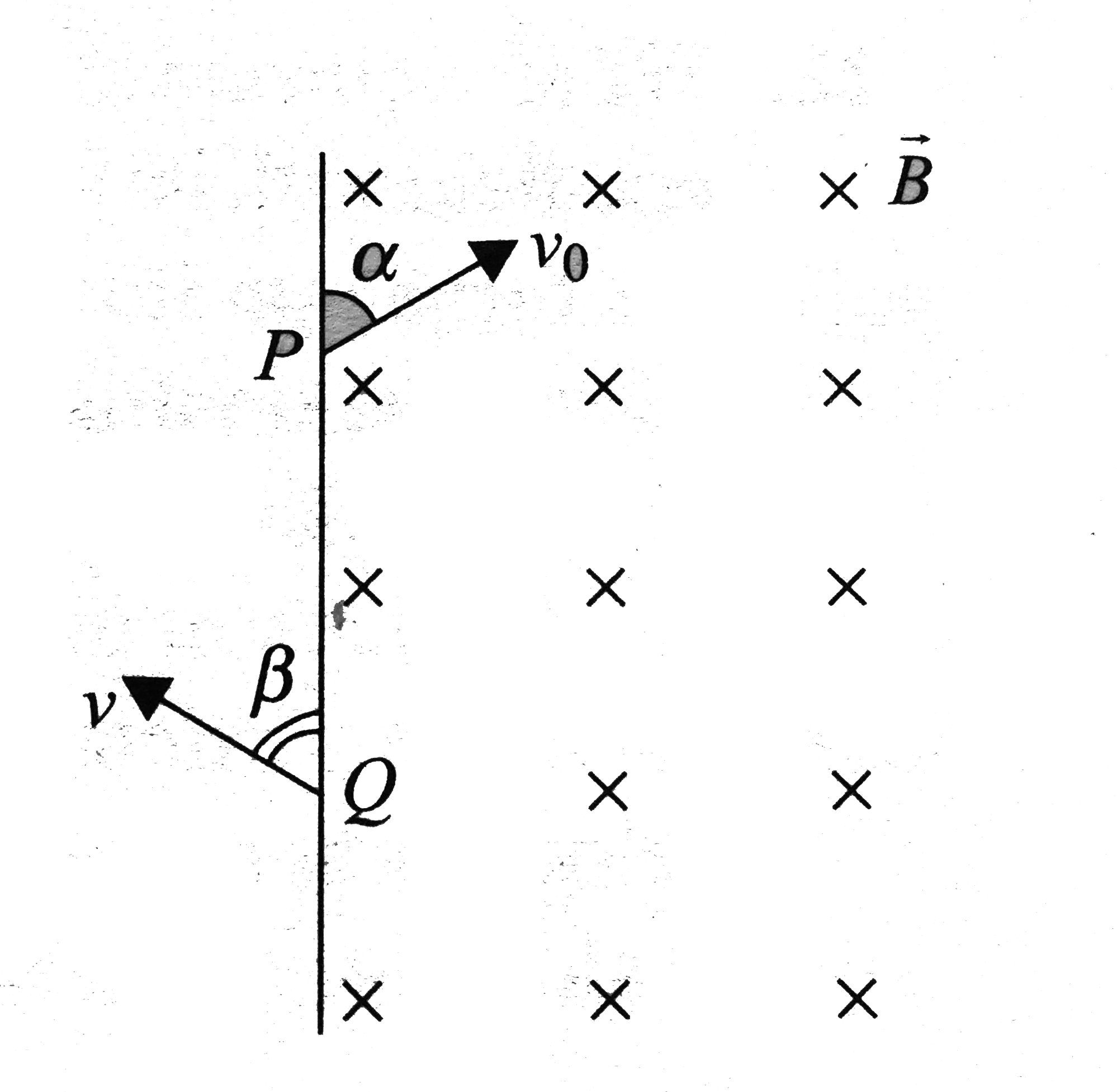 Aα=βBv=v0CPQ=2mv0sinαBqDThe particle remains in field for time t=2m(π−α)Bq
Aα=βBv=v0CPQ=2mv0sinαBqDThe particle remains in field for time t=2m(π−α)BqA charged particle enters a magnetic field B with its initial velocity v making an angle of π4 and B. The path of the particle will be
Aa straight lineBa circleCan ellipseDa helix
A positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.
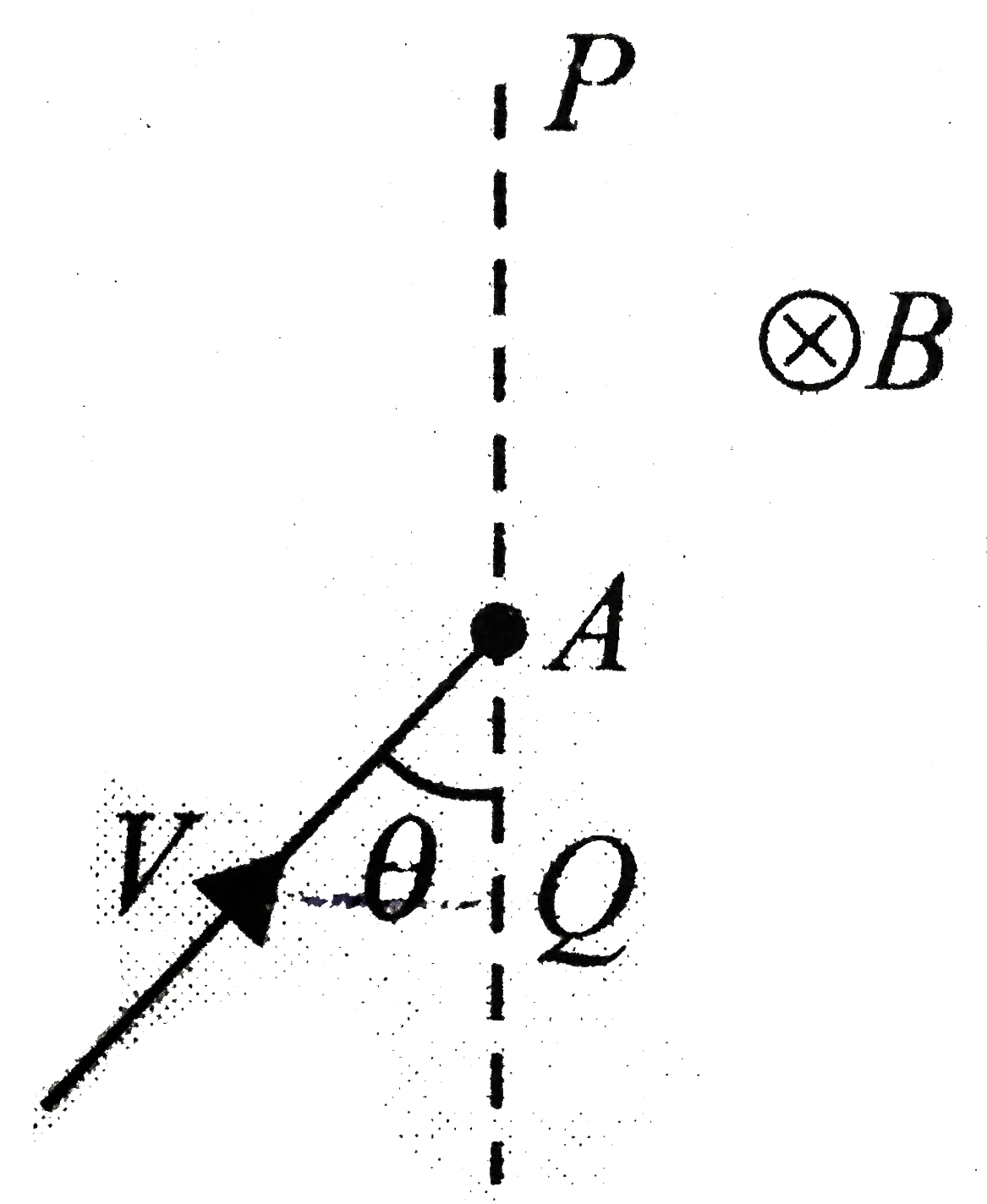
View SolutionA particle of charge q and mass m is prjected in a uniform and contant magnetic field of strength B.The initial velocity →v makes angle θ with the →B.Find the distance travelled by the particle in time t.
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
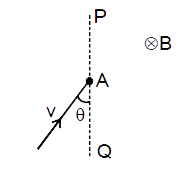
distance travelled in the magnetic field
View SolutionA particle of charge q and mass m, is fired perpenducular to a magnetic field (B) with a velocity v. What is the frequency of revolution of the particle?
View SolutionA proton of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B.The radius of curvature of the resulting path is
View Solution

