Two conducting concentric, hollow spheres A and B have radii a and b respectively, with A inside B. Their common potentials is V. A is now given some charge such that its potential becomes zero. The potential of B will now be
0
V(1−a/b)
Va/b
Vb/a
The correct Answer is:B
To solve the problem, we need to analyze the situation of two concentric conducting hollow spheres, A and B, with radii a and b respectively. The potential of sphere A is made zero by giving it a certain charge. We need to find the new potential of sphere B.
1. Understanding the Initial Conditions:
- Initially, both spheres A and B have a common potential V.
- Since they are conducting spheres, the electric field inside each conductor is zero, meaning the potential is constant throughout the conductor.
2. Charge Distribution:
- Let’s assume sphere B has an initial charge QB and sphere A has an initial charge of zero.
- The potential V of sphere B can be expressed as:
V=kQBb
where k is Coulomb's constant.
3. Applying Charge to Sphere A:
- Sphere A is given a charge QA such that its potential becomes zero.
- The potential VA of sphere A is given by:
VA=kQAa+kQBb=0
This means:
kQAa=−kQBb
Simplifying this gives:
QA=−abQB
4. Calculating the New Potential of Sphere B:
- The potential of sphere B after the charge is added to sphere A can be calculated using the new charge distribution.
- The potential VB of sphere B is now influenced by both its own charge and the charge on sphere A:
VB=kQBb+kQAb
Substituting QA:
VB=kQBb−k(abQB)b
Simplifying this:
VB=kQBb−kaQBb2
Factoring out kQBb:
VB=kQBb(1−ab)=kQBb⋅b−ab
Thus, we can express it as:
VB=V(1−ab)
5. Final Expression:
- Therefore, the potential of sphere B after sphere A is given a charge such that its potential becomes zero is:
VB=V(1−ab)
- Initially, both spheres A and B have a common potential V.
- Since they are conducting spheres, the electric field inside each conductor is zero, meaning the potential is constant throughout the conductor.
- Let’s assume sphere B has an initial charge QB and sphere A has an initial charge of zero.
- The potential V of sphere B can be expressed as:
V=kQBb
where k is Coulomb's constant.
- Sphere A is given a charge QA such that its potential becomes zero.
- The potential VA of sphere A is given by:
VA=kQAa+kQBb=0
This means:
kQAa=−kQBb
Simplifying this gives:
QA=−abQB
- The potential of sphere B after the charge is added to sphere A can be calculated using the new charge distribution.
- The potential VB of sphere B is now influenced by both its own charge and the charge on sphere A:
VB=kQBb+kQAb
Substituting QA:
VB=kQBb−k(abQB)b
Simplifying this:
VB=kQBb−kaQBb2
Factoring out kQBb:
VB=kQBb(1−ab)=kQBb⋅b−ab
Thus, we can express it as:
VB=V(1−ab)
- Therefore, the potential of sphere B after sphere A is given a charge such that its potential becomes zero is:
VB=V(1−ab)
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Exercise 24.1
Explore 4 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Exercise 24.2
Explore 9 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Example Type 8
Explore 3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:All Questions
Explore 120 Videos
Similar Questions
Two spheres A and B of radius a and b respectively are at the same potential. The ratio of the surface charge density of A to B is
View SolutionThree concentric spherical conductors A, B and C of radii R, 2R and 4R respectively. A and C is shorted and B is uniformly charged .
Potential at B is

View Solution
Knowledge Check
Two spheres A and B of radius 'a' and 'b' respectively are at same electric potential. The ratio of the surface charge densities of A and B is
AabBbaCa2b2Db2a2In the given circuit the potential at point B is zero, the potential at points A and D will be
 AVA=4V,VD=9VBVA=3V,VD=4VCVA=9V,VD=3VDVA=4V,VD=3V
AVA=4V,VD=9VBVA=3V,VD=4VCVA=9V,VD=3VDVA=4V,VD=3VEqual charges are given to two spheres of different radii . The potential will be
Amore on smaller sphereBmore on bigger sphereCequal on both the sphereDnone of these
Three concentric spherical conductors A, B and C of radii R, 2R and 4R respectively. A and C is shorted and B is uniformly charged
Potential at A is

View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
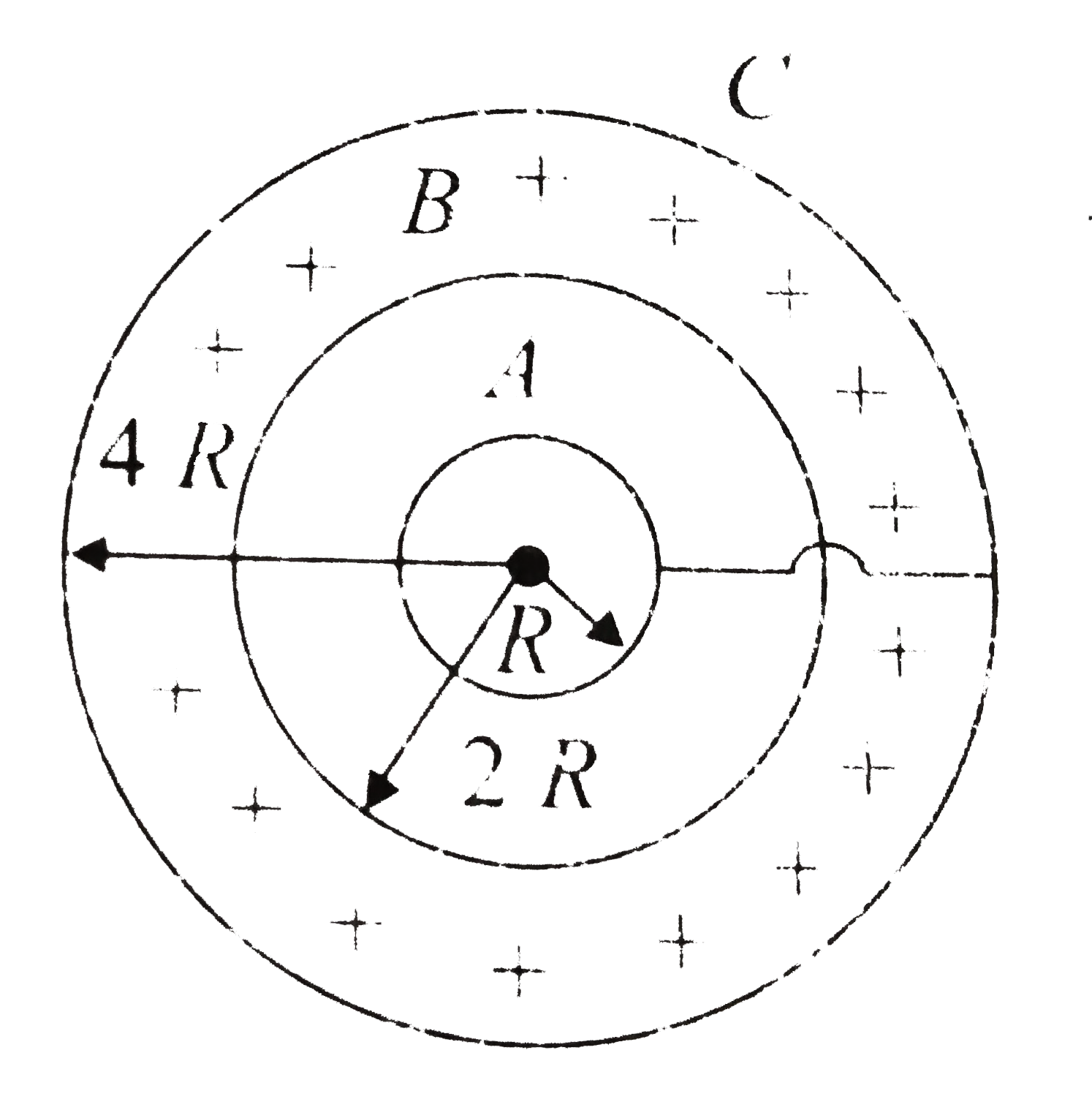
Potential at B is
View SolutionTwo copper spheres A and B of same radii, one hollow and the other solid are charged to the same potential. Which of the two will hold more charge
View SolutionA hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
View SolutionEqual charges are given to two spheres of different radii. The potential will
View Solution